



Tähega algavad funktsiooni rakenduse puhul kirjutatakse funktsiooninimi argumentide ette ehk prefixselt. Näiteks täisarvulise jagamise funktsioon div saab rakendada niimoodi: div 10 2.
Sümboliga algava funktsiooni rakenduse puhul kirjutatakse funktsiooninimi argumentide vahele ehk infixselt. Näiteks liitmise operaatorit + saab rakendada niimoodi: 10 + 2.
Kui me tahame tähega algavat funktsiooni kirjutada infixselt, peame funktsiooninime kirjutama tagurpidi ülakomade (‘) vahele. Näiteks võime kirjutada 10 `div` 2. Kui aga tahame sümboliga algavat operaatorit kirjutada prefixselt, peame selle ümbritsema selle sulgudega. Näiteks saame kirjutada (+) 10 2.
Infixoperaatoreid saab ka ise juurde defineerida:
| (@) :: Int -> Int -> Int x @ y = 2*x+y |
Pane Tähele!
Ka funktsiooni tüübikonstruktor -> on Haskelli standardi järgi infixne opertaator. Selle tüübikonstruktori esimene argument on funktsiooni sisendi tüüp ja teine argument funktsiooni väljundi tüüp.
Infixne rakendus on üldjuhul mitmeti mõistetav. Näiteks, mis on avaldise 2+3*4 väärtus? Tulemus sõltub sellest, kas lugeda seda avaldist kui 2+(3*4) või kui (2+3)*4. Sellise mitmesuse lahendamiseks on Haskellis kaks vahendit: prioriteedid (i.k precedence) ja assotsatiivsus. Mõlemat saab juhtida nn. fixity deklaratsiooniga.
Kasutades GHCI käsku “:i” saame defineeritud operaatorite kohta infot küsida. Haskelli standardteegis on muuhulgas defineeritud järgnevad fixity deklaratsioonid.
| infixl 6 + infixl 7 * infixl 7 / infixr 8 ^ infix 4 == |
Deklaratsioon infixl näitab vasak-assotsatiivsust, infixr parem-assotsatiivsust ning infix assotsiatiivsuse puudumist. Number näitab prioriteeti. Niisiis on korrutamisele antud suurem prioriteet — korrutamine seob tugevamini kui liitmine.
Infix operaatori assotsatiivsus läheb vaja siis, kui sama taseme operaatorit on mitmekordselt rakendatud. Näiteks, kas 10/2*3 on (10/2)*3 või 10/(2*3). Prioriteedid siin ei aita, kuna korrutamisel ja jagamisel on mõlemal prioriteet seitse. Nii jagamine kui korrutamine on vasak-assotsatiivsed, kuna nende fixity on defineeritud infixl. Seega paneme sulud vasakule ehk õige on (10/2)*3 !
Pane Tähele!
Funktsiooni tüübikonstruktor (->) on parem-assotsiatiivne.
Seetõttu on funktsiooni f :: Int -> Char -> Bool tüüp on
tegelikult sama mis tüüp Int -> (Char -> Bool) ehk saades argumendiks
näiteks täisarvu 5 tagastatakse funktsioon
f 5 :: Char -> Bool mis teeb tähtedes tõeväärtuseid.
Pane Tähele!
Kõige kõrgem prioriteet on alati prefixsel funktsioonirakendusel. Sealhulgas võime funktsioonile prefixselt argumendi rakendamisel lisaks panna sulud nii funktsiooni kui argumendi ümber. Niisiis, maksimaalselt sulge pannes on div 5 6 + 4 == ((((div) (5)) (6)) + (4))
Vahetevahel on tarvis kirjutada funktsioone, mis tagastavad korraga mitu väärtust. Näiteks võime tahta arvutada listi minimaalse ja maksimaalset elementi, listi vaid üks kord läbides. Standardne lahendus on tagastada arvude paar.
| minmax :: [Int] -> (Int, Int) minmax [x] = (x,x) minmax (x:xs) = (min x a, max x b) where (a,b) = minmax xs |
Paari tüüp ja paari väärtus luuakse tavapärases notatsioonis — sulgude vahel, komaga eraldatult. Paari andmestruktuurist andmete kättesaamiseks saab teha mustrisobitust. Aga kuna paari tüübiga andmestruktuur peab olema paar, siis pole tarvis teha hargnemist erinevate mustrite järgi. Alternatiivide puudumisel saame kasutada definitsiooni m = e, kus m on avaldise e tüübile vastav ainuke muster.

Teine võimalus paaride seest info saamiseks on kasutades standardteegi abifunktsioone fst :: (a,b) -> a ja snd :: (a,b) -> b mis tagastavad vastavalt paari esimese ja teise komponendi. Need funktsioonid on implementeeritud mustrisobitamisega.
Sarnaselt paaridele saame kasutada kolmikuid ning ka suuremaid ennikuid.
Kui paarid (5,True) :: (Int, Bool) on kahe komponendiga ennikud (ehk n=2), siis väärtused ise (5) :: (Int) võime tinglikult nimetada üksikuks (ehk n=1). Aga mis on nullikud (kus n=0)?
Nullikuid nimetatakse tegelikul hoopis unit-iks, kuna unit tüübil on ainult üks väärtus () :: (). Seda tüüpi kasutatakse sarnaselt void tüübiga C-keelte perekonnas. Tühjad sulud ei sisalda mingit informatsiooni ning seda on sobilik kasutada siis, kui vormiliselt tuleb mingi väärtus edastada aga tegelikult seda vaja ei ole.
Pane Tähele!
Niisama sulgude lisamine avaldise ümber ei muuda väärtust ega tüüpe. S.t. (Int) on sama mis Int.
Funktsionaalsetes keeltes on järjendid populaarsed, kuna selle definitsioon on lühike ja selge ning järjendeid saab kasutada erineva otstarbe jaoks. Eriotstarbeliste järjendite (iteraatorid, massiivid, topeltseotud ahelad, jne.) asemel kasutatakse funktsionaalses keeles esimese lähendusena liste.
Listil on kaks konstruktorit: tühja listi konstruktor “[]” ja mittetühja listi konstruktor “:”. See tähendab seda, et liste võime ette kujutada puudena, milles on listi elemendid ning konstruktorite [] ja : alamtipud.
[1, 2, 3] =
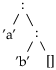 | ['a', 'b'] =
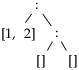 |
[[1, 2], []] =
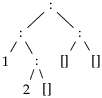
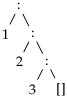
Pane Tähele!
Vahetipu “:” parem alam on alati listi element ja vasak ülejäänud list.
Mittetühja listi esimenest elementi kutsutakse tema peaks (i.k. head) ja järgnevaid elemente sabaks (i.k. tail). Haskelli standardteegis on listi pea ja saba leidmiseks vastavad funktsioonid.
head (
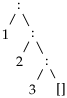 ) ⇝
1
| tail (
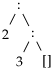 ) ⇝
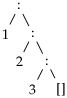 |
Haskelli süntaksis kirjutatakse andmete puustruktuure niimoodi, et kõigepealt tipu nimi ning seejärel alamad funktsiooni argumendina. Sümboliga algavaid nimesid (näiteks “:”) kirjutatakse aga hoopis infiks-selt ehk argumentide vahele. Kui tahame sellist nime kasutade prefiks-selt ehk argumentide ees, peame ümbritsema nime sulgudega. Seega kehtivad järgnevad võrdused.
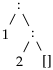
== 1 : (2 : (3 : [])) == (:) 1 ((:) 2 ((:) 3 []))
Lisaks võib mittetühja listi konstruktori paremalt poolelt sulud ära jätta, kuna see on defineeritud parem-assotsiatiivseks. S.t 1:(2:(3:[]])) = 1:2:3:[].
Listi tüüp on [α], mille iga element on tüübiga α. Näiteks täisarvude list [3,2,1] on tüüpi [Int] ja ujukomaarvu listide list [[1.0, 1.1], [1.2]] on tüüpi [[Float]]. Mingi tüübi omamist kirjutatakse ::-abil, ehk ['a', 'b'] :: [Char].
Tühja listi (konstruktori) [] tüüp on [a]. See tähendab, et a asemel võib mõelda ükskõik millise konkreetse tüüpi.
Kui funktsioon tahab argumendiks tõeväärtuste liste (e. [Bool]) siis võib anda argumendiks [].
Mittetühja listi konstruktori “:” tüüp on a -> [a] -> [a]. See operaator võtab elemendi ning sama tüüpi elementide listi ning tagastab listi, mille peaks on esimene argument ja sabaks teine.
0 : (
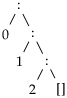
) ⇝
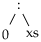
Kui andmestruktuuride loomiseks on vaja rakendada konstruktoreid, siis sellele vastupidiseks tehteks on mustrisobitus, mis võimaldab listist informatsiooni kätte saada. Muster on sobitatava listiga sama tüüpi puu, kus osad (vahe)tipud võivad olla asendatud muutujanimedega.
[]
xs
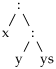
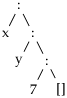
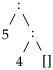
Kui mustrit kõrvutada mingi konkreetse listiga, saab otsustada, kas andmed vastavad mustrile või mitte. Ütleme, et muster sobitub andmetega, kui mustris olevatele muutujatele saab anda väärtuse nii, et see on võrdne etteantud listiga.
Näiteks list
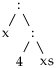
sobitub mustriga
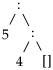
kui võtta x = 5 ja xs = [].
Samas list
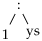
ei sobitub mustriga
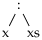
ühegi ys väärtuse korral.
Niisiis saame mustrisobitusega teada, kas mustrit saab andmetega sobitada ning kui jah siis milliste muutujate väätruse korral.
Oletame, et me tahame kirjutada listi kõikide elementide summa leidmise funktsiooni, piisab vaadata kahte juhtu (mustrit). Kui list on tühi, siis on selles olevate arvude summa null. Kui list pole tühi, liidame selle pea ja saba elementide summa.
sum [] = 0
sum (
) = x + sum xs
ehk siis teksti kujul nii
| sum [] = 0 sum (x:xs) = x + sum xs |
Mustrisobitusese teostamiseks võib olla abi mustri ja listi kohakuti kirjutamine ja sulgudega puustruktuuri rõhutamine. Näiteks, kui meil on muster (x:2:ys) ja listiks on [1,2,3,4] on tulemus.
| muster: | x : 2 : ys |
| list : | 1 : 2 : (3 : 4 : [])
|
Ehk siis muster sobitub ja muutujate väärtused peavad olema x = 1 ja ys = 3:4:[]. Edasi vaatame selle funktsiooni väärtustamist mõnel listil. Kuigi see pole kohustuslik, võime esimese sammuna listi teisendada konstruktorite rakenduse kujule — siis on mustrisobitus ehk selgemine arusaadav.
|
Ühe argumendiga listifunktsiooni on väga tihti mõistlik defineerida just mustrite [] ja (x:xs) järgi. Samas pole see alati nii. Võtame näiteks funktsiooni last :: [a] -> a mis tagastab mittetühja listi puhul viimase elemendi ja tühja puhul annab veateate. Kõige lihtsam oleks seda defineerida järgnevalt.
| last (x:[]) = x last (_:xs) = last xs |
Ehk siis üheelemendilise listi korral tagastatakse see ainuke element ja suurema listi korral kutsutakse välja sama funktsioon argumendi saba peal. Pane tähele, et funktsiooni ei defineerita tühjal listil, mistõttu annaks funktsiooni väljakutse sel juhul veateate.
Vaatame arvutuskäiku.
|
Pane Tähele! Kuna teisel juhul polnud listi pea väärtust vaja, kirjutame mustrisse muutujanime asemel alakriipsu.
Kuna järjendite definitsioon on rekursiivne (mittetühjal listil on saba, mis on omakorda list), siis on listide töötlemise funktsioonid enamasti ka rekursiivsed. Järgnevalt anname mõned näpunäited, kuidas ülesandeid lahendades tulla korrektse rekursiivse lahenduse peale.
Rekursioon on mingis mõttes sarnane induktsiooniga tõestustega: neil on baas ja samm. Rekursiooni baas tähendab seda, et kui me tahame kirjutada funktsiooni, mis termineerub, peame defineerima juhu kus rekursioon otsa saab. Listide puhul tähendab see enamasti tühja listi mustri juhtu, näiteks definitsiooni sum [] = 0 või last (x:[]) = x. Nendel juhtudel ei tohi rekursiivset kutset kasutada.
Rekursiivset kutset ei ole enamasti mõtekas teha täpselt samade argumendiga, mis funktsioon eelnevalt sai — see tekitaks lõpmatu tsükli. Vaatame näiteks järgmist ebakorrektselt implementeeritud summeerimisfunktsiooni.
| sumwrong [] = 0 sumwrong (x:xs) = x + sumwrong (x:xs) |
|
See funktsioonikutse ei termineeru.
Niisiis tuleb rekursiivne kutse sooritada väiksema argumendiga nii, et see jõuaks alati baasjuhule lähemale. Listide puhul on rekursiivne kutse tavaliselt lühema listiga ja täisarvulise funktsiooni puhul nullile lähema arvuga. Näiteks sum (x:xs) = x + sum xs ja last (x:xs) = last xs.
Kuidas aga leida õiget definitsiooni rekursiooni sammu jaoks? Tuleb mõelda, kuidas väiksemal argumendi lahendust teisendada algse argumendi lahenduseks. Vaatame näiteks faktoriaali funktsiooni fact :: Integer -> Integer. On selge, et iga argumendi n≥ 0 korral fact n peab olema sama mis n!, mis on defineeritud kui
| n! = n * (n−1) * (n−2) * … * 2 * 1 . |
Sel puhul on väga selge baasjuht, kus n=0. Ning kuna 0! = 1 siis fact 0 = 1. Aga kuidas leida sammu ehk juhtu n>0? Lahendus on eeldada, et rekursiivne kutse on juba korrektne ehk fact (n−1) = (n−1)!. Jääb üle mõelda, mis operatsiooniga saab (n−1)!-st teisendada n!. Aga loomulikult n! = n * (n−1)!. Seega saamegi järgneva lahenduse.
| fact 0 = 1 fact n = n * fact (n-1) |
Kahjuks pole eelnevalt mainitud meetod alati otse rakendatav. Näiteks, kui võtame endale ülesandeks kirjutada funktsioon kolmnulli :: [Int] -> Bool, mis tagastab True kui argumentlistis leidub vähemalt kolm nulli ja False kui leidub vähem kui kolm nulli. Siis sellise ülesande puhul ei saa me rekursiooni sammu kirjutada. Listis esimese nulli leidmise järel peaksime edasi uurima, kas sabas on vähemalt kaks nulli — aga meil on ainult funktsioon kolmnulli. Sellisel juhul tuleb kasutada loovat lähenemist ja mõelda välja abifunktsioon, mis on rekursiivselt kirjutatav ja mida saab kasutada meie ülesande lahendamisel. Näiteks nii
| kolmnulli xs = nullideArv xs >= 3 where nullideArv [] = 0 nullideArv (x:xs) | x==0 = 1 + nullideArv xs | otherwise = nullideArv xs |
Pane Tähele! Paljusid listiülesandeid on lihtsam lahendada, kui oskate kasutada standardteegis olevaid funktsioone. Infot standardteegis olevate võimaluste kohta saab lugeda siit: https://hackage.haskell.org/package/base/docs/Prelude.html
Haskellis on sõned defineeritud kui tähtede listid. Seega kehtivad järgnevad võrdused.
Ehk, "tere" = ['t','e','r','e'] = 't':'e':'r':'e':[].
Ning kuna Haskell ei suuda tähtede listie eristada sõnedest, siis trükitakse tähtede liste välja samuti kui sõnesid.
| *Main> 't':'e':'r':'v':'i':'s':'t':'!':[] "tervist!" |
Pane Tähele!
Haskelli Char-tüüp sisaldab kõiki Unicode sümboleid. Võime kirjutada näiteks
'∅' :: Char.
Mitmetel järjestatavatel elemenditüüpidel on kasutatav nn. enumeratsioonisüntaks. Vaatame järgmiseid näiteid.
|
Enumeratsioonide puhul on otspunktid (näites 5 ja 12) vaikimisi kaasaarvatud, väljaarvatud juhul, kui enumeratsiooni samm (näites 7−5) sellest "üle astub". Samm defineerib, mitmest elemendist tuleb üle astuda. Ülemise punkti olemasolul ei väljastata sellest suuremaid elemente, s.t. [10, 20 .. 15] ⇝
[10].
Enumeratsioon on defineeritud tüüpidel Int, Integer, Char, Bool, (), Float ja Double. Väheste elementidega tüüpide puhul ei saa ka “lõpmatu” enumeratsioon olla tegelikult lõpmatu, s.t. [False ..] ⇝
[False, True].
Pane Tähele!
Kuna Haskell on laisk keel, ei tekita lõpmatud listid ilmtingimata probleemi. Juhul kui arvutuse tulemuse jaoks läheb vaja vaid lõpliku osa, ei arvutata vahetulemust täiel määral välja. Näiteks head [5..] ⇝
5.
Nagu algselt mainitud, on Haskell funktsionaalne keel, mis tähendab et funktsioonid on samuti “tavalised” väärtused. Samamoodi nagu me saame arvutada numbritega, peame saama arvutada ka funktsioonidega.
Kuna funktsioon saab tagastada täisarvu, peab funktsioon saama tagastada ka funktsiooni. Tegelikult me seda juhtu juba oleme vaadanud. Iga funktsioon, mis võtab mitu argumenti, võtab tegelikult esimese argumendi ja siis tagastab funktsiooni, mis võtab järgnevad argumendid. Näiteks võime defineerida järgnevad funktsioonid.
| liida :: Int -> Int -> Int liida x y = x + y suurenda :: Int -> Int suurenda = liida 1 |
|
Kuna funktsiooni liida võtab kõigepealt ühe argumendi x ja tagastab seejärel funktsiooni, mis võtab teise argumendi y, siis saame defineerida funktsiooni suurenda, andes funktsioonile liida ainult esimese argumendi.
Pane Tähele!
Funktsiooni suurenda oleks saanud ka defineerida nii:
| suurenda :: Int -> Int suurenda x = liida 1 x |
Miks kasutada osalist rakendamist? Vastus: et vältida kordust ehk üleliigset koodi. Samal põhjusel ei kirjuta me if x < 5 == True then … vaid ikka if x < 5 then ….
Ka infixseid funktsioone saab Haskellis osaliselt rakendada — seda nimetatakse sekstsiooniks. Eelneva näite funktsioone saab defineerida hoopis nii
| suurenda :: Int -> Int suurenda = (1 +) |
või ka nii
| suurenda :: Int -> Int suurenda = (+ 1) |
Kuna funktsioon saab argumendiks võtta täisarvu, peab saama võtta ka teise funktsiooni. Järgnevalt vaatleme standardfunktsiooni operaatorit (.), mis on defineeritud järgnevalt.
| (.) :: (b -> c) -> (a -> b) -> a -> c (f . g) x = f (g x) |
Funktsioonide komponeerimise operaator (.) võtab esimeseks argumendiks funktsiooni, mis teeb b-dest c-sid, ja teiseks argumendiks funktsiooni, mis teeb a-dest b-d. Tagastatakse funktsioon, mis teeb a-dest c-d.
Selle abil saame defineerida järgneva funktsiooni:
| suurendaRohkem :: Int -> Int suurendaRohkem = suurenda . (*2) |
|
Edasijõudnud Haskelli programmeerijad kirjutavad listifunktsioone väga tihti kõrgemat järku funktsioonide: map, filter, takeWhile, dropWhile, foldr jne.
Sellise stiiliga saab kirjutada väga selget koodi: kohe peale vaadates on näha erinevad sammud. Nii saame mõttes tegeleda kogu listiga korraga. Tsükli või rekursiooniga kirjutatud listi teisendud on lihtsam olulisi detaile kahe silma vahele jätta.
Viimastes Haskelli versioonides on äsja loetletud funktsioonide tüüpe muudetud, tehes neid üldisemaks. Siin vaatleme esmalt, kuidas need kõrgemat järku funktsioonid oleks defineeritud listidel.
mapSee funktsioon rakendab etteantud teisendust kõikidele sisendlisti elementidele.
| map :: (a -> b) -> [a] -> [b] map f [] = [] map f (x:xs) = f x : map f xs |
Funktsiooni map definitsiooni meelde jätmise asemel on targem hoopis keskenduda järgnevale võrdusele.
map f [x1, x2, …, xn] = [f x1, f x2, …, f xn]
Vaatame näiteks järgneva avaldise väärtustust.
|
filterSee funktsioon võtab esimese argumendiga predikaadi (ehk funktsiooni mis tagastab tõeväärtuse) ning tagastab sisendlistist vaid need elemendid, kus predkiaat kehtib (ehk tagastab True).
| filter :: (a -> Bool) -> [a] -> [a] filter p [] = [] filter p (x:xs) | p x = x : filter p xs | otherwise = filter p xs |
Vaatame näiteks järgneva avaldise väärtustust, mis kasutab täisarvu predikaati even. Funktsioon even tagastab True parajasti siis, kui argument on paarisarv.
|
take* ja drop*Listi algusosa saab listist eraldada funktsioonidega take ja takeWhile. Sümmeetriliselt take* funktsioonidega tagastavad drop* funktsioonid ülejäänud listi osa. Esmalt vaatame funktsioone mis eraldavad listist mingi kindla arvu elemente.
| take :: Int -> [a] -> [a] take n [] = [] take n (x:xs) | n <= 0 = [] | otherwise = x : take (n-1) xs drop :: Int -> [a] -> [a] drop n [] = [] drop n (x:xs) | n <= 0 = xs | otherwise = drop (n-1) xs |
Kolme esimese elemendi võtmine listist käib nii.
|
Kolme esimese elemendi eemaldamine listist aga nii.
|
Teine võimalus on eraldada listi osi mingi tingimuse abil. Funktsioon takeWhile võtab esimese argumendina predikaadi ning tagastab funktsiooni algusest elemente kuni predikaat tagastab False.
| takeWhile :: (a -> Bool) -> [a] -> [a] takeWhile p [] = [] takeWhile p (x:xs) | p x = x : takeWhile p xs | otherwise = [] dropWhile :: (a -> Bool) -> [a] -> [a] dropWhile p [] = [] dropWhile p (x:xs) | p x = dropWhile p xs | otherwise = x:xs |
Vaatame listist elementide eemaldamist predikaadiga isSpace, mis tagastab True parajasti siis kui argument on tühikusümbol.
|
foldrSee funktsioon on listi andmetüübi rekursor, mis tähendab, et kõiki (rekursiivseid) listifunktsioone on võimalik foldr abil mitterekursiivselt kirjutada.
| foldr :: (a -> b -> b) -> b -> [a] -> b foldr f a [] = a foldr f a (x:xs) = f x (foldr f a xs) |
Nii saab listi elementide summa või korrutise defineerida ühe lühikese reaga.
| summa = foldr (+) 0 korrutis = foldr (*) 1 |
Summa arvutamise arvutuskäik on näiteks selline.
|
Listi pikkust saab defineerida nii.
| pikkus = foldr f 0 where f x n = n+1 |
Summa arvutamise arvutuskäik on näiteks selline.
|
Järgnevalt püüame aru saada, kuidas lihtsad Haskelli programmid käivitamisel toimivad. Väikeste programmide juures polnud arvutusmudeli puudumine suurem probleem, kuna saime funktsioone GHCI-s jooksvalt testida. Suuremaid programme kirjutades tuleb kasuks täpselt teada, kuidas meie poolt programmeeritud arvutus toimub.
Arvutusmudelis on kesksel kohal programm, ehk programmi kõik definitsioonid. Lisaks vastavas käsitletavas programmifailis olevatele definitsioonidele on programmi osaks enamasti ka standardteegist tulev moodul Prelude.
| double x = x+x main = double (5*5) |
Siin on kaks definitsiooni: funktsioon double ja väärtus main. Muidugi on programmis ka standarteegi definitsioon liitmise ka korrutamise kohta, mida eelnevalt mainitud definitsioonid kasutavad.
Arvutusmudeli töö seisneb valitud avaldise järk-järgulises teisendamises. Kompileeritud programmi puhul on selleks avaldiseks lihtsalt main. GHCi-d kasutades saab suvalis avaldisi süsteemil väärtustada lasta.
Päris Haskelli interpreteerimisel ja kompileerimisel kasutatakse vahekeelt, mille nimeks on System Fω, milles on esitatavad kõik Haskelli programmid. Vahekeele kasutamise põhjuseks on süntakitliste struktuuride ja erireeglid eemaldamine või vähendamine.
Meie vaatame samuti lihtsustatud keelt, kus saab kasutada aritmeetikat ja liste. Erinevalt keelest System Fω on meie keel ilma tüüpideta aga süntaktiliselt lähedasem väga lihtsale Haskellile. Kuigi lihtsustatud keeles pole andmetüüpe, eeldame et programmid on saadud tüübikorrektsetest Haskelli programmidest.
Keele avaldised võivad olla muutujad, avaldiste ennikud, (aritmeetilised) konstandid, binaarsed (aritmeetilised) avaldised, listikonstruktorid ja funktsioonikutsed.
|
Mustriks võib olla alakriips (_), muutujanimi, konstant, mustrite ennik või mustrite list.
|
Programm koosneb deklaratsioonidest kujul:
|
Aga iga nime deklaratsioon võtab sama arvu parameetreid. Nii saame ühe nime deklaratsioonid koguda sellisteks gruppideks.
|
| length [] | = 0 |
| length (_ : xs) | = 1 + length xs |
| append [] xs | = xs |
| append (x : xs) ys | = x : append xs ys |
Avaldise väärtustamine käib sammudena, kus mingi alamavaldis lihtsustatakse kindlate reeglite järgi. Lihtsustusreegleid on meil kaks: a) aritmeetiline tehe asendamine konstandiga ja b) funktsiooni keha asendamine funktsioonikutse asemele.
|
Väärtustamise esimene samm tuli teha põhjusel, et otsustada, millist length definitsiooni kasutada. Selle järel on selge, et saame kasutada length teist võrrandit. Seejärel peame jälle tegema sammu length argumendiga.
Avaldisest redutseeritavate alamavaldiste (ehk reedeksite) leidmiseks võtame ette avaldise abstraktse süntaksipuu. Järgmise reedeksi leidmiseks kasutame järjestust, mis on omapärane segu lõpp- ja eesjärjestusest. Kui süntaksipuu tipuks on aritmeetiline tehe, mida me saame teostada vaid siis, kui tema argumendid on leitud, või konstruktor kasutame lõppjärjestust (i.k. post-order). See tähendabki seda, et kõigepealt arvutame argumendid vasakult paremale ja siis teeme aritmeetilise tehte või konstruktori rakenduse.
Vastasel juhul kasutame eesjärjestust (i.k. pre-order) ehk hakkame tegelema süntaksipuu tipuga. Kui tipuga mingil põhjusel tegeleda ei saa, näiteks me ei oska valida, millist funktsiooni võrdust kasutada, arvutame valimist takistavaid argumente suunaga vasakult paremale.
Kuigi rääkisime järjestusest, mis läbiks kogu struktuuri, on meil vaja leida vaid esimene lihtsustatav alamavaldis. Seejärel lihtsustame seda alamavaldist ja paneme algsesse avaldisse tagasi ning alustame uuesti reedeksi otsimist.




Kui peame lihtsustama funktsioonikutset f e1 … en ja oleme leidnud sobiva definitsiooni
| f p1 … pn = b |
siis saame teha teisenduse
| f e1 … en ⟶ b[p1 → e1]…[pn → en] |
kus kandiliste sulgudega tähistatakse asenduse tegemist (defineeritud järgmises alampeatükis).
| definitsioon: | length (_: xs ) = 1 + length xs |
| avaldis: | length (1: 2: []) |
| 1. vahesamm: | (1 + length xs)[(_: xs) → (1: 2: [])] |
| 2. vahesamm: | (1 + length xs)[xs → (2: [])] |
| tulemus: | 1 + length (2: []) |
Nüüd defineerime täpselt asendamise operaatorit e1[p→e2], mis tagastab e1 koopia, kus muster p on asendatud avaldisega e2.
Alakriipsu, konstantide ja tühja listi asendus jätab avaldise muutmata.
|
Ennikute ja mittetühjade listide puhul asendame komponenthaaval.
|
Asendatava muutuja asendame, teised jätame samaks.
|
Konstandid ei sisalda muutujaid ja jäävad seega samaks.
|
Ülejäänud juhtudel asendame komponente rekursiivselt.
|
Funktsiooni võrrandite süntaksiga on ühendatud funktsioonide defineerimine ja mustrisobitus. Kui aga võrrandite juurde lubada kirjutada valvureid, läheb väärtustamise defineerimine keeruliseks. Nimelt, valvurite kontrollimine ei toimu üldjuhul ühe sammuga, mistõttu on meil vaja kasutada süntaksit, kus valvurite arvutus saab olla poolel teel.
| f xs | all (>0) xs = f (map (-1) xs) | otherwise = xs |
Avaldise f [2,3] väärtustamisel peame valvuri abil otsustama, kumma haru kodiga avaldis asendada. Valvuri väärtustamine pole aga triviaalne ehk ühe sammuga tehtav.
Sellistel puhkudel kasutame võrrandite asemel case-of süntaksit, mis tegeleb mustrisobituse ja valvuritega. Vaatame juhtu, kus väärtustatav avaldis on järgneval kujul:
| case e of p1 | b1 -> e1 ... pn | bn -> en |
kus pi on mustrid, bi tõeväärtusavaldised ja ei avaldised. Kui valvurit vaja pole, kasutame väärtust True.
Kui muster p1 sobib, tuleb omakorda vaadata kolme järgnevat juhtu
b1 ≡ True siis saame kogu case avaldise asendada e1[p1 → e]-ga.
b1 ≡ False siis kustutame selle case juhu.
b1[e → p1]
| case Just 5 of Nothing -> 0 Just x | even x -> 1 Just x | odd x -> x |
Kuna Nothing ei sobitu väärtusega Just 5 siis kustutame selle.
| case Just 5 of Just x | even x -> 1 Just x | odd x -> x |
Kuna aga teise juhu tingimus pole True ega False, peame seda väärtustama. Niisiis lihtsustame avaldist (even x)[x → 5] = even 5 → False.
Tulemus on järgnev.
| case Just 5 of Just x | False -> 1 Just x | odd x -> x |
Seekord, aga, on valvur False, mistõttu kustutame selle juhu.
| case Just 5 of Just x | odd x -> x |
Sarnaselt eelmisele korrale peame enne valvurit väärtustama. Niisiis lihtsustame avaldist (odd x)[x → 5] = odd 5 → True.
Tulemus on järgnev.
| case Just 5 of Just x | True -> x |
Nüüd on valvur True, mistõttu saame kogu case-avaldise asendada väärtusega x[x → 5] ehk siis 5.


