NB! Kõik joonised ei ole html-versioonis korralikud. Soovija leiab nad pdf või ps failidest minu publikatsioonide lehelt
Helger Lipmaa1
Date: 17. detsember 1998. a.
Lähtudes Church-Turingi printsiibist saab ülesandeid keerukusklassidesse jagada vastavalt sellele, kui efektiivsed algoritmid nende ülesannete jaoks on põhimõtteliselt võimalikud (näiteks) Turingi masinatel.
Öeldakse, et (determineeritud, stohhastiline) algoritm töötab (determineeritud, stohhastilises) polünomiaalses ajas (DPA, SPA), kui leidub selline polünoom p, nii algoritmi tööks kuluv aeg on väiksem kui p(| x|) suvalise sisendi x jaoks.
Kui ülesande X jaoks leidub determineeritud (stohhastiline) polünomiaalse
keerukusega algoritm, öeldakse, et see ülesanne on lahenduv
determineeritud (stohhastilises) polünomiaalses ajas ning kirjutatakse
X ![]()
![]() (
X
(
X ![]()
![]() ).
).
Keerukusklassi
![]() kuuluvaid ülesandeid samastatakse tavaliselt
``lihtsate'' ehk ``efektiivselt lahenduvate'' ülesannetega.
kuuluvaid ülesandeid samastatakse tavaliselt
``lihtsate'' ehk ``efektiivselt lahenduvate'' ülesannetega.
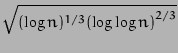 ) .
) .
Seega, kvantmehaanika efektide arvestamine ei pruugi olla mitte ainult kasulik, vaid muutuda ka paratamatuks.
``Kvantarvutid on pööratavad arvutid''.
Hulka X nimetatakse meetriliseks ruumiks, kui igale tema elementide
paarile x, y ![]() X on vastavusse seatud reaalarv
X on vastavusse seatud reaalarv ![]() (x, y) nii, et on
täidetud tingimused:
(x, y) nii, et on
täidetud tingimused:
Meetrilist ruumi nimetatakse täielikuks, kui temas iga Cauchy jada koondub.
Olgu
![]() =
= ![]() või
või
![]() =
= ![]() . Suvalise
a + bi
. Suvalise
a + bi ![]()
![]() korral
korral
![]() = a - bi on arvu x
kaaskompleksarv. Kui
= a - bi on arvu x
kaaskompleksarv. Kui
![]() =
= ![]() , siis
, siis
![]() = x,
= x,
![]() x.
x.
Vektorruumi H üle korpuse
![]() nimetatakse skalaarkorrutisega
ruumiks, kui igale elemendipaarile x, y
nimetatakse skalaarkorrutisega
ruumiks, kui igale elemendipaarile x, y ![]() H on vastavusse seatud
kindel arv
H on vastavusse seatud
kindel arv
![]() x| y
x| y![]()
![]()
![]() , mida nimetatakse elementide x ja
y skalaarkorrutiseks, nii, et on täidetud järgmised tingimused:
, mida nimetatakse elementide x ja
y skalaarkorrutiseks, nii, et on täidetud järgmised tingimused:
Kvantsüsteemi olekuruumi saab kirjeldada lainefunktsioonide Hilberti
ruumina. Kvantarvutuste jaoks on vaja vaid lõplikumõõtmelisi
vektorruume üle korpuse
![]() . Sellistel olekuruumidel leiduvad
(Gram-Schmidti ortogonaliseerimisprotsess) ortonormeeritud baasid, mida
tähistatakse Dirac'i bra/ket notatsiooni kasutades järgmiselt:
. Sellistel olekuruumidel leiduvad
(Gram-Schmidti ortogonaliseerimisprotsess) ortonormeeritud baasid, mida
tähistatakse Dirac'i bra/ket notatsiooni kasutades järgmiselt:
Vektorruumi suvaline element | x![]() avaldub baasivektorite | 0
avaldub baasivektorite | 0![]() ja
| 1
ja
| 1![]() lineaarse kombinatsioonina
a| 0
lineaarse kombinatsioonina
a| 0![]() + b| 1
+ b| 1![]() =
= ![]() , kus
a,
b
, kus
a,
b ![]()
![]() ning a2 + b2 = 1. Selles tähistuses on
ning a2 + b2 = 1. Selles tähistuses on
![]() x| y
x| y![]() võrdne vektorite
võrdne vektorite
![]() x| ning | y
x| ning | y![]() skalaar- ehk
sisekorrutisega,
| x
skalaar- ehk
sisekorrutisega,
| x![]()
![]() y| on aga nende vektorite
väliskorrutis: 2×2 unitaarmaatriks, mida võib standardsel
viisil vaadelda lineaarkujutusena. Näiteks
y| on aga nende vektorite
väliskorrutis: 2×2 unitaarmaatriks, mida võib standardsel
viisil vaadelda lineaarkujutusena. Näiteks
Kvantbitt (qubit) on normeeritud vektor
kahemõõtmelises vektorruumis üle korpuse
![]() , mille jaoks
on fikseeritud konkreetne baas
{| 0
, mille jaoks
on fikseeritud konkreetne baas
{| 0![]() ,| 1
,| 1![]() }. Baasolekud
| 0
}. Baasolekud
| 0![]() ja | 1
ja | 1![]() vastavad klassikalistele bitiväärtustele 0 ja 1.
vastavad klassikalistele bitiväärtustele 0 ja 1.
Erinevalt klassikalistest bittidest võivad kvantbitid olla
superpositsioonis, st kvantbiti iga väärtus kujul
a| 0![]() + b| 1
+ b| 1![]() ,
a2 + b2 = 1, on lubatud. Superpositsiooni mõõtmisel fikseeritud
baasi
{| 0
,
a2 + b2 = 1, on lubatud. Superpositsiooni mõõtmisel fikseeritud
baasi
{| 0![]() ,| 1
,| 1![]() } järgi saadakse tõenäosusega a2 tulemuseks
vektor | 0
} järgi saadakse tõenäosusega a2 tulemuseks
vektor | 0![]() ning tõenäosusega b2 tulemuseks vektor | 1
ning tõenäosusega b2 tulemuseks vektor | 1![]() .
.
Ühes kvantbitis on võimalik kodeerida vaid ühte klassikalist bitti, st informatsiooniteooria vaatenurgast sisaldub ühes kvantbitis täpselt sama palju informatsiooni kui ühes klassikalises bitis.
Võtmekehtestusprotokolli eesmärgiks on genereerida salajane võti, mida edasises suhtluses kaks osapoolt saaksid kasutada andmete krüptimiseks. Võimatu ilma eelneva ühisteadmuseta (eelnevalt vahetatud salajane võti, mida kasutades vahetatakse uus võti), kui ei toetu arvutuslikele eeldustele (näiteks: faktoriseerimine on raske). Põhjuseks on tõestatavalt turvaliste kanalite mitteleidumine ``klassikalises maailmas.'' Ehk: kõik on põhimõtteliselt pealtkuulatav. Kvantkanali lisamisel muutub salajane võtmekehtestus võimalikuks.
Iga footoni saabumisel valib Bob juhuslikult kas baasi
![]() (0) või
(0) või
![]() (1), mille järgi seda footonit mõõta. Pärast bittide edastamist
avalikustavad Alice ning Bob oma baasidevalikud. Kui n-nda baasi valik
ühtis (tõenäosus
(1), mille järgi seda footonit mõõta. Pärast bittide edastamist
avalikustavad Alice ning Bob oma baasidevalikud. Kui n-nda baasi valik
ühtis (tõenäosus
![]() ), võetakse n-is bitt kasutusele, vastasel
juhul mitte.
), võetakse n-is bitt kasutusele, vastasel
juhul mitte.
Kui Eve soovib lugeda protokolli i-ndat bitti, peab ta seda tegema mingi
baasi
![]() (Ei) järgi. Kuna Alice valis baasid juhuslikult, on
Eve jaoks parim strateegia ka ise baasid juhuslikult valida. Sellisel
juhul valib Eve õige baasi tõenäosusega
(Ei) järgi. Kuna Alice valis baasid juhuslikult, on
Eve jaoks parim strateegia ka ise baasid juhuslikult valida. Sellisel
juhul valib Eve õige baasi tõenäosusega
![]() ning saab
teada biti tegeliku väärtuse.
ning saab
teada biti tegeliku väärtuse.
Tõenäosusega
![]() valib Eve vale baasi ning seega on mõõtmise
tulemuseks juhuslik suurus hulgast
{| 0
valib Eve vale baasi ning seega on mõõtmise
tulemuseks juhuslik suurus hulgast
{| 0![]() ,| 1
,| 1![]() }. Vale baasi
järgi mõõtmine muudab footoni ning seega on ``nuhitud'' footonil erinev
polarisatsioon kui mittenuhitud footonil.
}. Vale baasi
järgi mõõtmine muudab footoni ning seega on ``nuhitud'' footonil erinev
polarisatsioon kui mittenuhitud footonil.
Lisaprotokollide (``salastuse võimendamine'') abil saavad Alice ja Bob hiljem klassikalist kanalit pidi informatsiooni vahetades ligikaudse hinnangu sellele, kas ja kuipalju bitte on keegi vahepeal pealt kuulanud.
| K | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| A | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| Footon |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| Footon |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| B | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| K | 0 | 1 | ? | 1 | ? | 1 | ? | 1 | ? | 0 | 0 | ? |
Klassikalistes arvutusmudelites (ja klassikalises füüsikas) moodustab
n osakesest koosnev süsteem, mille iga osake on vektor kahemõõtmelises
vektorruumis, kokku 2n-mõõtmelise vektorruumi:
dim(U×V) = dim U + dim V. Kvantsüsteemis on saadava vektorruumi dimensioon ent 2n:
dim(U ![]() V) = dim U . dim V. Nii on näiteks kolmest kvantbitist
koosneva süsteemi baasiks
V) = dim U . dim V. Nii on näiteks kolmest kvantbitist
koosneva süsteemi baasiks
Paralleelsuse eksponentsiaalne kasv tuleneb sellest, et kõik
n + m-mõõtmelised vektorid ei avaldu n- ja m-mõõtmeliste vektorite
tensorkorrutisena. Tõestame, et olek
![]() (| 00
(| 00![]() + | 11
+ | 11![]() )
ei avaldu kahe vektori tensorkorrutisena.
)
ei avaldu kahe vektori tensorkorrutisena.
| (a1| 0 |
= | |
| a1a2| 00 |
. |
Selliseid olekuid nimetatakse sasiolekuks (ka sidusolek, entangled state); ainult logaritmiline osa kõikidest olekutest ei ole sasiolekud; neil olekutel ei ole klassikalises füüsikas analoogi ning just nende tõttu tekib kvantparallelism. Eelnevast tuleneb ka see, et isegi väikese kvantsüsteemi simuleerimine klassikalistel arvutitel nõuab eksponentsiaalse arvu olekute jälgimist.
Kvantarvutite potentsiaali põhjuseks on kvantolekute evolutsiooni kasutamine arvutusmehhanismina.
Kvantsüsteemi parameetri(te) mõõtmise tulemuseks on süsteemi normaalprojektsioon olekuruumi mõõdetud väärtustega ühilduvasse alamruumi (``Von Neumanni projektsioonihüpotees''). Normaalprojektsioon -- pärast mõõtmist saadud süsteemi olekuvektor on endiselt üks. Öeldakse, et mõõtmisel olek kollapseerub.
Seejärel projekteerub olek alamruumi, mis on ühilduv mõõdetud
tulemusega (| 0![]() ), uus olekuvektor normeeritakse ning seega saadakse
tulemuseks uus olek
), uus olekuvektor normeeritakse ning seega saadakse
tulemuseks uus olek
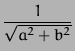 (a| 00
(a| 00
Saab tõestada, et osakesed ei ole sasiolekus ![]() ühe osakese mõõtmine
ei mõjuta teist osakest (teine, ekvivalentne definitsioon). Nii
on
ühe osakese mõõtmine
ei mõjuta teist osakest (teine, ekvivalentne definitsioon). Nii
on
![]() (| 00
(| 00![]() + | 11
+ | 11![]() ) sasiolek, kuna enne
teise osakese mõõtmist on esimese osakese mõõtmise tulemuseks tõenäosusega
) sasiolek, kuna enne
teise osakese mõõtmist on esimese osakese mõõtmise tulemuseks tõenäosusega
![]() vektor | 0
vektor | 0![]() . Pärast teise osakese mõõtmist on
aga esimese osakese mõõtmise tulemuseks | 0
. Pärast teise osakese mõõtmist on
aga esimese osakese mõõtmise tulemuseks | 0![]() või | 1
või | 1![]() tõenäosusega 1 sõltuvalt sellest, kas teise osakese mõõtmisel
saadi tulemuseks | 0
tõenäosusega 1 sõltuvalt sellest, kas teise osakese mõõtmisel
saadi tulemuseks | 0![]() või | 1
või | 1![]() .
.
Anname Alice'ile ning Bobile ühe osakese sasiosakeste paarist. Seejärel teostab Alice oma osakesel mõõtmise. Seejärel mõõdab Bob oma osakest ning saab hetkeliselt vastuseks sama tulemuse, mis Alice, sõltumatult Alice'i ja Bobi vaheliselt kauguselt. Tundub, et tegu on paradoksiga (informatsiooni liikumine valgusest kiiremini). On siiski võimalik näidata, et Alice'il ja Bobil ei ole nii võimalik valgusest kiiremini informatsiooni vahetada.
Seega, ehkki füüsikas on EPR-paradoks tunnetuslikult väga oluline (lokaalsuse printsiip, kvantmehaanika interpretatsioonid), ei ole kvantarvutite seisukohalt tegemist paradoksiga.
Mittemõõdetud kvantsüsteem areneb vastavalt Schrödingeri võrrandile, olekud
muutuvad olekuteks, säilitades ortogonaalsust. Vektorruumis üle korpuse
![]() on ortogonaalsust säilitavateks lineaarteisendusteks
unitaarteisendused. Lineaarteisendused on esitatavad maatriksitena. Maatriks
M on unitaarne (vastab unitaarteisendusele) kui MM* = 1, kus M*
on maatriksi M konjugeeritud maatriksi transponeeritud maatriks.
Kvantolekute ruumi unitaarsed teisendused vastavad (üksüheselt) legaalsetele
kvantteisendustele. Vastavalt unitaarteisenduste definitsioonile,
on ortogonaalsust säilitavateks lineaarteisendusteks
unitaarteisendused. Lineaarteisendused on esitatavad maatriksitena. Maatriks
M on unitaarne (vastab unitaarteisendusele) kui MM* = 1, kus M*
on maatriksi M konjugeeritud maatriksi transponeeritud maatriks.
Kvantolekute ruumi unitaarsed teisendused vastavad (üksüheselt) legaalsetele
kvantteisendustele. Vastavalt unitaarteisenduste definitsioonile,
Esitame järgnevas tabelis neli kõige elementaarsemat kvantlüli (quantum gates) koos nende alternatiivsete definitsioonidega.
| Samasusteisendus | I |
| 0 |
|
| Eitus | X |
| 0 |
|
| Faasinihe | Z |
| 0 |
|
| Faasinihke eitus | Y = Z . X |
| 0 |
|
Ühebitiseid kvantoperatsioone kujutatakse graafiliselt operatsiooni nimega märgendatud kastina:
Olgu

Joonisel on kujutatud kahe kvantbitine lüli, kus esimese biti väärtusest sõltuvalt teise biti väärtus muutub või mitte.
Lüli juhitav-juhitav-eitus (Toffoli lüli), kus kolmanda biti väärtus muutub vaid siis kui esimesed kaks bitti on mõlemad 1, kujutatakse järgmiselt:
Hadamard'i teisendus on järgmine:
| H(| 0 |
: = |
|
| H(| 1 |
: = |
| W| 00...0 |
||
| = | ||
| = |
Olgu U -- klooniv unitaarteisendus:
U(| x0![]() ) = | xx
) = | xx![]() iga
x jaoks. Olgu a ning b kaks ortogonaalset kvantolekut. Siis
U(| a0
iga
x jaoks. Olgu a ning b kaks ortogonaalset kvantolekut. Siis
U(| a0![]() ) = | aa
) = | aa![]() ,
U(| b0
,
U(| b0![]() ) = | bb
) = | bb![]() . Olgu
c : =
. Olgu
c : = ![]() (| a
(| a![]() + | b
+ | b![]() ). Lineaarsusest
). Lineaarsusest
Olgu Alice'il esimene ning Bobil teine sasiosake EPR-paarist
1/2(| 00![]() + | 11
+ | 11![]() ). Tihe kodeerimine kasutab ühte
kvantbitti koos eelnevalt ``vahetatud'' EPR-paariga kahe klassikalise biti
kodeerimiseks ning edastamiseks. Seega kulub hiljem kahe klassikalise biti
edastamiseks vaid üks tavaline bitt. Üllatav, kuna teame, et
informatsiooniteoreetiliselt kvantbitt=bitt!
). Tihe kodeerimine kasutab ühte
kvantbitti koos eelnevalt ``vahetatud'' EPR-paariga kahe klassikalise biti
kodeerimiseks ning edastamiseks. Seega kulub hiljem kahe klassikalise biti
edastamiseks vaid üks tavaline bitt. Üllatav, kuna teame, et
informatsiooniteoreetiliselt kvantbitt=bitt!
| Väärtus | Teisendus | EPR-paari uus olek |
| 0 |
|
|
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| Algolek | Juhitav eitus | 1. bitt | 2. bitt |
|
|
|
|
| 0 |
|
|
|
|
| 1 |
|
|
|
|
| 1 |
|
|
|
|
| 0 |
Seejärel mõõdab Bob teise kvantbiti väärtuse (kvantolek ei kollapseeru!).
Kui mõõtmise tulemus on | 0![]() , siis kodeeritud väärtus oli 0 või 3,
kui mõõtmise tulemus on | 1
, siis kodeeritud väärtus oli 0 või 3,
kui mõõtmise tulemus on | 1![]() , siis kodeeritud väärtus oli 1 või 2.
, siis kodeeritud väärtus oli 1 või 2.
Bob rakendab esimesele osakesele teisenduse H.
| Algolek | 1. bitt | H(1. bitt) |
|
|
| 0 |
|
|
|
| 0 |
|
|
|
| 1 |
|
|
|
| 1 |
Mõõtes esimese biti väärtuse, suudab Bob eristada väärtusi 0 ja 3, 1 ja 2.
Vastand tihedale kodeerimisele -- ühe kvantbiti edastamiseks kasutatakse kahte klassikalist bitti. Üllatav, kuna võimaldab teisaldada tundmatu kvantbiti väärtust (kloonimise võimatus!). On realiseeritud eksperimentaalselt.
Enne protokolli algust on Alice'il esimene ning Bobil teine osake
EPR-paarist. Alice soovib edastada kvantbitti
![]() : = a| 0
: = a| 0![]() + b| 1
+ b| 1![]() , kasutades klassikalisi kanaleid.
Kvantsüsteemi algolek on
, kasutades klassikalisi kanaleid.
Kvantsüsteemi algolek on
| = |
||
| = |
Alice rakendab algolekule järjestikku teisendusi
Cnot ![]() I ja
H
I ja
H ![]() I
I ![]() I (ehk tiheda kodeerimise dekodeerimissammu):
I (ehk tiheda kodeerimise dekodeerimissammu):
| (H | ||
| = (H |
||
| = (H |
||
| = |
||
| = |
Alice mõõdab esimesed kaks kvantbitti, saades väärtuse
|![]()
![]() ,
,
![]()
![]() {0,..., 3}. Alice saadab mõõtmise tulemused kui kaks
klassikalist bitti Bobile. Vastavalt Alice'i mõõtmise tulemustele
projekteerub Bobi kvantbitt üheks neljast väärtusest
a| 0
{0,..., 3}. Alice saadab mõõtmise tulemused kui kaks
klassikalist bitti Bobile. Vastavalt Alice'i mõõtmise tulemustele
projekteerub Bobi kvantbitt üheks neljast väärtusest
a| 0![]() ±b| 1
±b| 1![]() ,
a| 1
,
a| 1![]() ±b| 0
±b| 0![]() .
.
Kvantbitte mõõtes muutis Alice taastamatult kvantbiti ![]() väärtust,
mistõttu biti teleportimine Bobile ei räägi vastu kloonimise
mittevõimalikkusele.
väärtust,
mistõttu biti teleportimine Bobile ei räägi vastu kloonimise
mittevõimalikkusele.
| Bitid | Olek | Dekodeerimine |
| 00 |
a| 0 |
I |
| 01 |
a| 1 |
X |
| 10 |
a| 0 |
Y |
| 11 |
a| 1 |
Z |
Teame, et kõik kvantteisendused on pööratavad. Kuigi klassikaline NOT tehe on pööratav, pole seda AND ega NAND tehted: teades, et lause ``A ja B'' on väär, pole võimalik teada saada, kumb komponentidest tegelikult väär oli. See probleem lahendatakse nn prügibittide kasutusele võtmisega.
Suvalise kahe unitaarteisenduse U ja V korral on unitaarne ka
tingimuslik teisendus
| 0![]()
![]() 0|
0| ![]() U + | 1
U + | 1![]()
![]() 1|
1| ![]() V.
V.
Cnot : = | 0![]()
![]() 0|
0| ![]() I + | 1
I + | 1![]()
![]() 1|
1| ![]() X.
X.
Kolmebitine juhitav-juhitav-eitus (ehk Toffoli lüli):
Järgmisel joonisel on toodud ühebitist liitjat implementeeriv kvantskeem, mis kasutab Toffoli lüli ning juhitavat eitust. Siin on x ning y liidetavad bitid, c on sisendülekanne, s on saadav summa (mod 2) ning c' on väljundülekanne.
Olgu
S : = | 00![]()
![]() 00| + | 01
00| + | 01![]()
![]() 10| + | 10
10| + | 10![]()
![]() 01| + | 11
01| + | 11![]()
![]() 11| --
vahetusoperaator. Fredkini lüli on ``juhitav vahetus'':
11| --
vahetusoperaator. Fredkini lüli on ``juhitav vahetus'':
Pööratavate kvantlülide abil saab arvutada kõiki klassikaliselt arvutatavaid funktsioone, järelikult on võimalik konstrueerida universaalne kvant-Turingi masin.
Kuna suvalist klassikalist funktsiooni f saab arvutada kvantarvutil,
võime eeldada seda funktsiooni arvutava kvantskeemi
Uf : | x, y![]()
![]() | x, y
| x, y ![]() f (x)
f (x)![]() olemasolu.
olemasolu.
Sedasi defineeritud skeem Uf on unitaarne suvalise funktsiooni f
jaoks. Väärtuse f (x) leidmiseks rakendame skeemi Uf sisendile
| x, 0![]() .
.
Kuna
f (x) ![]() f (x) = 0, siis
UfUf = I ning seega
Uf on pööratav.
f (x) = 0, siis
UfUf = I ning seega
Uf on pööratav.
Kuigi T- ja F-lülid on täielikud klassikaliste arvutuste jaoks, ei piisa neist suvaliste kvantarvutuste teisendamiseks. Viimaste jaoks tuleb primitiivsete skeemide hulka lisada ka ühebitised rotatsioonid.
Olgu
Ry(![]() ) : =
) : = ![]()
![]()
![]() (rotatsioon
(rotatsioon
![]() radiaani ümber y-telje),
Rz(
radiaani ümber y-telje),
Rz(![]() ) : =
) : = ![]()
![]()
![]() (rotatsioon
(rotatsioon
![]() radiaani ümber z-telje),
Ph(
radiaani ümber z-telje),
Ph(![]() ) : =
) : = ![]()
![]()
![]() (faasinihe
(faasinihe ![]() võrra).
võrra).
Lemma. Iga unitaarset 2×2 maatriksit
M ![]() U(2) saab
avaldada kujul
Ph(
U(2) saab
avaldada kujul
Ph(![]() )Rz(
)Rz(![]() )Ry(
)Ry(![]() )Rz(
)Rz(![]() ),
), ![]() ,
,
![]() ,
, ![]() ja
ja
![]()
![]()
![]() . Iga unitaarset maatriksit M,
det M = 1 (st
M
. Iga unitaarset maatriksit M,
det M = 1 (st
M ![]() SU(2)), saab avaldada kujul
Rz(
SU(2)), saab avaldada kujul
Rz(![]() )Ry(
)Ry(![]() )Rz(
)Rz(![]() ).
).
Tõestus. Kuna maatriks on unitaarne ![]() maatriks rea- ja veeruvektorid on
ortonormaalsed, siis avaldub iga
M
maatriks rea- ja veeruvektorid on
ortonormaalsed, siis avaldub iga
M ![]() U(2) kujul
U(2) kujul

Seega saab kõiki ühekvantbitiseid kvantarvuteid emuleerida, kasutades vaid rotatsioone ning faasinihkeid. On näidatud, et mitmekvantbitiste arvutite korral piisab, kui lisada tehetele juhitav-eitus.
Rakendame skeemi Uf sisendite superpositsioonile. Kuna Uf on lineaarteisendus, ``rakendub'' Uf simultaanselt kõigile superpositsioonis olevatele sisenditele. Seetõttu on võimalik välja arvutada funktsiooni f väärtused kõikvõimalikel sisenditel, rakendades skeemi Uf sisendite superpositsioonile üksainus kord.
Kõik kvantparallelismi kasutavad kvantalgoritmid peavad järgima
fikseeritud plokkskeemi. Alustatakse n-kvantbitisest olekust
| 00...0![]() . Algolekule rakendatakse teisendust W,
misjärel saadakse olek
. Algolekule rakendatakse teisendust W,
misjärel saadakse olek
Lineaarsuse tõttu
Vaatleme juhtu f = T:
Tulemust võib vaadata kui funktsiooni tõeväärtuste tabelit ehk kui
funktsiooni graafikut. Väärtused x, y ja x![]() y on seotud sellisel
moel, et tulemuse mõõtmine annab teada tõeväärtuste tabeli ühe rea ehk
funktsiooni graafiku ühe punkti. Mõõtmine projekteerib oleku kõigi
selliste sisendväärtuste y superpositsiooni, mil f (y) = f (x).
y on seotud sellisel
moel, et tulemuse mõõtmine annab teada tõeväärtuste tabeli ühe rea ehk
funktsiooni graafiku ühe punkti. Mõõtmine projekteerib oleku kõigi
selliste sisendväärtuste y superpositsiooni, mil f (y) = f (x).
Kaks tuntumat kvantparallelismi kasutamise meetodit on:
Olgu
| x![]() =
= ![]() (| 0
(| 0![]() + | 1
+ | 1![]() ) ning
| y
) ning
| y![]() =
= ![]() (| 0
(| 0![]() -| 1
-| 1![]() ),
),
| Uf| xy |
= Uf |
|
| = |
||
| = |
Paljusid probleeme saab formuleerida kui otsiprobleeme kujul ``leida selline x, et P(x) oleks tõene'' (ülesanded andmebaasi päringutest kuni graafi värvimiseni).
Teatud tüüpi probleemide korral on teada mingi abistav lisainformatsioon, mida saab kasutada tõhusa lahendusalgoritmi leidmiseks: paljude otsiülesannete (graafi värvitavus, elemendi otsing järjestatud listis) on otsinguruum struktureeritud, sellistel juhtudel saab ülesande täislahendi kätte teatud alamprobleemide lahendite kombineerimisel.
Üldjuhul, lisastruktuuride puudumisel, puudub täielikust läbivaatusest parem algoritm: kui otsinguruumi suurus on N, kulub struktureerimata otsinguks O(N) sammu.
Grover, 1997: stohhastiline kvantalgoritm, mis kulutab struktureerimata
otsinguks
O(![]() ) sammu (tõestatud, et parim võimalik algoritm).
) sammu (tõestatud, et parim võimalik algoritm).
Hogg: Groveri algoritmi saab kiirendada struktureeritud otsinguruumide jaoks. Hoggi algoritmid on juba nii keerukad, et nende õnnestustõenäosust pole siiamaani suudetud määrata ja seega pole ka teada Hoggi algoritmi täpne keerukus.
Tavaliselt leitakse heurilistiliste algoritmide efektiivsus empiiriliste meetodite arvutil testides. Kvantarvutide puhul võimatu -- simuleerimiseks kulub eksponentsiaalne aeg. Väikeste sisendite puhul on Hoggi algoritm Groveri algoritmist kiirem (polünomiaalselt). Kuni pole ehitatud kvantarvuteid või pole leitud paremaid matemaatilisi meetodeid selliste algoritmide analüüsimiseks, ei ole seega täpse keerukuse määramine võimalik.
Groveri algoritm teostab otsingut struktureerimata listis võimsusega N.
Olgu n naturaalarv, 2n > N. Olgu n-bitine predikaat P
teostatud kvantskeemina
Up : | x, 0![]()
![]() | x, P(x)
| x, P(x)![]() , kus viimase biti
väärtus on 1
, kus viimase biti
väärtus on 1 ![]() P(x) on tõene. Groveri algoritmi esimene samm on
standarne: sisendile
| 0...0
P(x) on tõene. Groveri algoritmi esimene samm on
standarne: sisendile
| 0...0![]() rakendatakse Walshi teisendust ning
seejärel skeemi Up, saades tulemuseks summma
A(P) = (1/2)n/2
rakendatakse Walshi teisendust ning
seejärel skeemi Up, saades tulemuseks summma
A(P) = (1/2)n/2![]() | x, P(x)
| x, P(x)![]() .
.
Suvalise sellise x0 korral, mille jaoks P(x0) on tõene, kuulub
| x0, 1![]() superpositsiooni A(P), kuid kuna selle oleku amplituud on
1/2n/2, on tõenäosus superpositsiooni mõõtmise järel suuruse x0
saamiseks
(1/2)n/2.
superpositsiooni A(P), kuid kuna selle oleku amplituud on
1/2n/2, on tõenäosus superpositsiooni mõõtmise järel suuruse x0
saamiseks
(1/2)n/2.
Groveri algoritmi järgmised sammud muudavad kvantolekut A(P) nii, et
olekute
| x, 1![]() (olekute, mille puhul P(x) on tõene) amplituud
suureneks oluliselt olekute
| x, 0
(olekute, mille puhul P(x) on tõene) amplituud
suureneks oluliselt olekute
| x, 0![]() amplituudide arvel.
amplituudide arvel.
Tänu amplituudi muutustele on tõenäosus, et mõõtmisel saadakse 1, suur.
Sellisel juhul projitseerub olek A(P) alamruumile
2-k/2![]() | xi, 1
| xi, 1![]() , kus k on lahendite arv. Esimese n
biti mõõtmine väljastab tulemuseks ühe nendest olekutest. Kui viimase biti
mõõtmisel saadakse tulemuseks 0, alustatakse kogu protsessi algusest
peale.
, kus k on lahendite arv. Esimese n
biti mõõtmine väljastab tulemuseks ühe nendest olekutest. Kui viimase biti
mõõtmisel saadakse tulemuseks 0, alustatakse kogu protsessi algusest
peale.
On tõestatud, et GA ja optimaalse algoritmi vahe ei ole suurem kui konstant
struktureerimata listide korral. Kui vaid ühe x0 korral on P(x0)
tõene, on
![]() /8
/8![]() sammu järel algoritmi õnnestumistõenäosus 0.5.
Pärast
sammu järel algoritmi õnnestumistõenäosus 0.5.
Pärast
![]() /4
/4![]() sammu on õ.t. 1 - 2-n. Huvitaval kombel väheneb
õ.t. pärast lisasamme: peale
sammu on õ.t. 1 - 2-n. Huvitaval kombel väheneb
õ.t. pärast lisasamme: peale
![]() /2
/2![]() sammu on õ.t. 2-n.
sammu on õ.t. 2-n.
Põhjendus: kvantalgoritmid on rotatsioonid kompleksruumis. Liiga suur pöördenurk kaugendab tulemust oodatust. Järelikult: itereeritud kvantteisenduste kasutamisel peab olema täpselt teada, millal lõpetada.
Olgu
A = ![]() ai. Teisendust
ai. Teisendust
![]() ai| xi
ai| xi![]()
![]()
![]() (2A - ai)| xi
(2A - ai)| xi![]() teostab N×N maatriks
teostab N×N maatriks




R-i saab leida O(log N) sammuga.
(Üldistus) Olgu P -- suvaline predikaat,
Up : | x, b![]()
![]() | b
| b ![]() P(x)
P(x)![]() . Olgu
|
. Olgu
|![]()
![]() = 2-n/2
= 2-n/2![]() | x
| x![]() .
Rakendame lüli Up superpositsioonile
|
.
Rakendame lüli Up superpositsioonile
|![]() , b
, b![]() , kus
b = 2-1/2(| 0
, kus
b = 2-1/2(| 0![]() - | 1
- | 1![]() ). Olgu
Xi = {x : P(x) = i}.
). Olgu
Xi = {x : P(x) = i}.
| Up(| |
= 2- (n + 1)/2Up( |
|
| = 2- (n + 1)/2( |
||
| = 2- (n + 1)/2( |
Kvantarvutite vastu tõusnud huvi üks peapõhjuseid oli kiire faktoriseerimisalgoritmi avastamine Peter Shori poolt 1994 aastal. Shori algoritm töötab randomiseeritud polünomiaalses ajas, olles järelikult sama keerukusastmega kui parimad (teadaolevad) algarvutestid. Veelgi enam -- Shori algoritmi keerukus (kui kõrvale jätta randomiseeritus) on täpselt sama, mis modulaareksponendi arvutamisel).
Arvestades sellega, et Shori algoritmi kordamisel suureneb tema õ.t. eksponentsiaalselt, võib pisut üldistades siiski öelda, et kvantarvutitel on ründed RSA-tüüpi krüptosüsteemi vastu täpselt niisama efektiivsed kui RSA-ga krüptimine; enamiku tänapäeva asümmeetriliste krüptosüsteemide kasutamine kaotab mõtte kvantarvutite saabumisel.
Asümmeetriline krüptograafia: kolm algoritmi -- võtmegeneraator G, krüptimisalgoritm e, dekrüptimisalgoritm d. Fikseeritud turvaparameeter k.
Alice genereerib võtmepaari (EA, DA), kus EA on avalik ning DA salajane võti ning avalikustab võtme EA (peab olema efektiivne).
Bob krüptib teate M, kasutades Alice'i avalikku võtit EA ning saadab teate C : = e(EA, M) Alice'ile (peab olema efektiivne).
Alice dekrüptib teate C, kasutades salajast võtit DA ning saab tulemuseks bitistringi d (DA, e(EA, C)) = M (peab olema efektiivne).
Ründaja soovib leida salajast võtit DA, teades võtit EA ning polünomiaalset paaride hulka (M, e(EA, M)) (peab olema ebaefektiivne).
Vaatleme konkreetselt RSA krüptosüsteemi. Olgu
![]() (x) = {y < x : gcd(y, x) = 1}. Alice genereerib kaks suurt algarvu p ja
q, ning leiab korrutise n. Seejärel genereerib Alice avaliku eksponendi
e, nii et
gcd(e,
(x) = {y < x : gcd(y, x) = 1}. Alice genereerib kaks suurt algarvu p ja
q, ning leiab korrutise n. Seejärel genereerib Alice avaliku eksponendi
e, nii et
gcd(e,![]() (n))=1 ning leiab (Eukleidese algoritmi kasutades)
salajase eksponendi d, nii et
ed
(n))=1 ning leiab (Eukleidese algoritmi kasutades)
salajase eksponendi d, nii et
ed ![]() 1(mod
1(mod ![]() (n)). Alice'i avalik
võti on EA = (n, e), Alice'i salajane võti on
(n, p, q, e, d ) (algarvutest
(n)). Alice'i avalik
võti on EA = (n, e), Alice'i salajane võti on
(n, p, q, e, d ) (algarvutest
![]()
![]() , Eukleidese algoritm
, Eukleidese algoritm
![]()
![]() ).
).
Avateksti M krüptogramm
e(EA, M) : = xemodn,
krüptogrammile M vastav avatekst
d (DA, M) : = xdmodn
(modulaareksponent
![]()
![]() ).
).
Kuna
![]() (n) = (p - 1)(q - 1), siis võimaldab n-i faktoriseerimine ründajal
leida suuruse
(n) = (p - 1)(q - 1), siis võimaldab n-i faktoriseerimine ründajal
leida suuruse ![]() (n) ning seejärel leida d, kasutades Eukleidese
algoritmi. Järelikult, kui faktoriseerimine on lihtne, on lihtne ka RSA
lahtimurdmine.
(n) ning seejärel leida d, kasutades Eukleidese
algoritmi. Järelikult, kui faktoriseerimine on lihtne, on lihtne ka RSA
lahtimurdmine.
Algoritmi alguses kasutatakse standardsel moel kvantparallelismi, leides funktsiooni f väärtused kõikvõimalikel sisenditel vastava kvantskeemi Uf ühekordse rakendamisega.
Seejärel leitakse funktsiooni f nn kvant-Fourier' teisendus (KFT). Pärast KFT rakendamist saab mõõtmisel suure tõenäosusega kätte funktsiooni f perioodi, mida kasutatakse järgnevas ``tava-algoritmi'' kasutades faktoriseerimiseks.
Diskreetne Fourier' teisendus teisendab väärtustehulgaga 0,
..., N - 1 funktsiooni g funktsiooniks Fg, piltlikult öeldes
``ajafunktsioon'' ``sagedusfunktsiooniks,'' mille väärtuste hulgaks on
lõigus [0, 2![]() ) asetsevad suuruse 2
) asetsevad suuruse 2![]() /N kordsed. Muuhulgas, kui
funktsiooni g periood on r, on tulemfunktsiooni Fg väärtus nullist
erinev vaid sageduse 1/r kordsetel sisenditel.
/N kordsed. Muuhulgas, kui
funktsiooni g periood on r, on tulemfunktsiooni Fg väärtus nullist
erinev vaid sageduse 1/r kordsetel sisenditel.
KFT opereerib kvantoleku amplituudidega, teisendades oleku
![]() g(x)| x
g(x)| x![]() olekuks
olekuks
![]() Fg(c)| c
Fg(c)| c![]() . Kui kvantolekut mõõta
pärast KFT rakendamist, saadakse tulem | c
. Kui kvantolekut mõõta
pärast KFT rakendamist, saadakse tulem | c![]() tõenäosusega
| Fg(c)|2.
Sealjuures on Fg(c) nullist erinev vaid suuruse N/r kordsetel
punktidel ning seega jagub mõõtmistulemus suurusega N/r.
tõenäosusega
| Fg(c)|2.
Sealjuures on Fg(c) nullist erinev vaid suuruse N/r kordsetel
punktidel ning seega jagub mõõtmistulemus suurusega N/r.
Kuna KFT on variant kahe astmetel baseeruvast kiirest Fourier' teisendusest, mis annab täpsed vastused vaid kahe astmele vastaval perioodil, on ka KFT tulemus ligikaudne, kui funktsiooni g periood ei ole kahe aste. KFT täpsus suureneb koos baasiks kasutatud kahe astme kasvuga, kvantskeem UKFT baasil 2m defineeritakse järgnevalt:
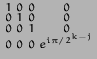
Kvantarvutite ehitamisel on fundamentaalseks probleemiks vajadus isoleerida kvantolek. Kvantbitte kandvate osakeste interaktsioon välise keskkonnaga rikub kvantolekut, põhjustades selle dekoherentsi (mitteunitaarseid teisendusi). Suvalise ehitatava kvantarvuti dekoherents on arvatavalt vähemalt 107 korda liiga suur, et rakendada Shori algoritmi 130-kohalistel arvudel.
Veaparandusalgoritmide lisamisel Shori algoritmile väheneb dekoherentsiefekt, mis teeb (teoreetiliselt) võimalikumaks piisavalt suurte süsteemide ehitamise.
Kvantveaparandus on väliselt sarnane klassikalise veaparandusega -- ``teksti'' lisatakse liiasust, mis võimaldab vigu avastada ja kõrvaldada. KVP on siiski keerulisem kui VP, kuna me ei tegele mitte kahendandmete, vaid kvantolekutega: KVP peab täpselt rekonstrueerima kodeeritud kvantoleku.
Kuna kvantolekut on võimatu kloonida ehk kopeerida, tundub rekonstruktsioon olevat keerulisem, kui klassikalisel juhul. Siiski, klassikalised tehnikad töötavad (modifitseeritult) kvantjuhul.
This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -local_icons -html_version 3.2,math,latin1 efs.tex
The translation was initiated by Helger Lipmaa on 2000-12-03