Abstract: The Fiat-Shamir construction (Crypto 1986) is an efficient transformation in the random oracle model for creating non-interactive proof systems and signatures from sigma-protocols. In classical cryptography, Fiat-Shamir is a zero-knowledge proof of knowledge assuming that the underlying sigma-protocol has the zero-knowledge and special soundness properties. Unfortunately, Ambainis, Rosmanis, and Unruh (FOCS 2014) ruled out non-relativizing proofs under those conditions in the quantum setting.
In this paper, we show under which strengthened conditions the Fiat-Shamir proof system is still post-quantum secure. Namely, we show that if we require the sigma-protocol to have computational zero-knowledge and statistical soundness, then Fiat-Shamir is a zero-knowledge simulation-sound proof system (but not a proof of knowledge!). Furthermore, we show that Fiat-Shamir leads to a post-quantum secure unforgeable signature scheme when additionally assuming a "dual-mode hard instance generator" for generating key pairs.
Abstract: We describe how classical security proofs for Fiat-Shamir go wrong in the quantum setting, and what can be done about it.
Abstract: We show the post-quantum security of the Fiat-Shamir construction (Crypto 1986), both as a proof system, and as a signature scheme. We circumvent the impossibility results from Ambainis, Rosmanis, and Unruh (FOCS 2014) by strengthening the assumptions about the underlying sigma-protocol
Abstract: In classical cryptography, one of the most important properties of hash functions is collision-resistance. We explain why collision-resistance is (often) not a sufficient requirement in the post-quantum setting, and present an alternative, the collapsing-property. We discuss the security of Merkle-Damgård-hashes (e.g., SHA2) and sponge-based hashes (e.g., SHA3): under which conditions are they collapsing? Finally, we study the "indifferentiability" of the sponge-construction (on which classical proofs are based), and present ongoing work for showing that the sponge-construction is not indifferentiable.
Abstract: Fiat-Shamir is a popular construction in classical cryptography for constructing signature schemes (and non-interactive proof systems). However, when considering security against quantum attackers, the security of Fiat-Shamir is largely unknown; all we know are negative results for various cases. In the present talk, we show progress towards a security proof for Fiat-Shamir. We introduce a new conjecture, the "Quantum Forking Conjecture" (QFC). The QFC is a problem in quantum query complexity. We show that if the QFC holds, then Fiat-Shamir is secure. This reduces a complex cryptographic question (involving quantum polynomial-time adversaries etc.) to a (hopefully simpler) query complexity problem.
Abstract: Fiat-Shamir is a popular construction in classical cryptography for constructing signature schemes (and non-interactive proof systems). However, when considering security against quantum attackers, the security of Fiat-Shamir is largely unknown; all we know are negative results for various cases. In the present talk, we show progress towards a security proof for Fiat-Shamir. We introduce a new conjecture, the "Quantum Forking Conjecture" (QFC). The QFC is a problem in quantum query complexity. We show that if the QFC holds, then Fiat-Shamir is secure. This reduces a complex cryptographic question (involving quantum polynomial-time adversaries etc.) to a (hopefully simpler) query complexity problem.
Abstract: We construct collapse-binding commitments in the standard model. Collapse-binding commitments were introduced by Unruh, Computationally binding quantum commitments, 2016 to model the computational-binding property of commitments against quantum adversaries, but only constructions in the random oracle model were known.
Furthermore, we show that collapse-binding commitments imply selected other security definitions for quantum commitments, answering an open question by (Unruh 2016).
Abstract: Commitment schemes are a fundamental primitive in cryptography. Their security (more precisely the computational binding property) is closely tied to the notion of collision-resistance of hash functions. Classical definitions of binding and collision-resistance turn out too be weaker than expected when used in the quantum setting. We present strengthened notions (collapse-binding commitments and collapsing hash functions), explain why they are "better", and show how they be realized under standard assumptions.
Abstract: Commitment schemes are a fundamental primitive in cryptography. Their security (more precisely the computational binding property) is closely tied to the notion of collision-resistance of hash functions. Classical definitions of binding and collision-resistance turn out too be weaker than expected when used in the quantum setting. We present strengthened notions (collapse-binding commitments and collapsing hash functions), explain why they are "better", and show how they be realized under standard assumptions.
Abstract: Commitment schemes are a fundamental primitive in cryptography. Their security (more precisely the computational binding property) is closely tied to the notion of collision-resistance of hash functions. Classical definitions of binding and collision-resistance turn out too be weaker than expected when used in the quantum setting. We present strengthened notions (collapse-binding commitments and collapsing hash functions), explain why they are "better", and show how they be realized under standard assumptions.
Abstract: In recent years, the computer-aided verification of cryptographic schemes has seen great progress. For example, various state-of-the-art cryptographic schemes were analyzed using the EasyCrypt tool using a probabilistic relational Hoare logic (pRHL). However, existing tools and logics are unsuited for analysis of quantum cryptographic protocols—be it protocols using quantum mechanics or protocols secure against quantum adversaries
In this talk, we explain why pRHL is not sound for quantum cryptography, and show how to lift the ideas from pRHL to the quantum setting.
Abstract: We present a new definition of computationally binding commitment schemes in the quantum setting, which we call "collapse-binding". The definition applies to string commitments, composes in parallel, and works well with rewinding-based proofs. We give simple constructions of collapse-binding commitments in the random oracle model, giving evidence that they can be realized from hash functions like SHA-3. We evidence the usefulness of our definition by constructing three-round statistical zero-knowledge quantum arguments of knowledge for all NP languages.
Abstract: In recent years, the verification of cryptographic schemes on the computational level (i.e., without symbolic abstractions) has seen great progress. For example, various state-of-the-art cryptographic schemes were analyzed using the EasyCrypt tool using a probabilistic relational Hoare logic (pRHL). However, existing tools and logics are unsuited for analysis of quantum cryptographic protocols – be it protocols using quantum mechanics, or protocols secure against quantum adversaries. In this talk, we explain why pRHL is not sound for quantum cryptography, and show how to lift the ideas from pRHL to the quantum setting. (With the long-term goal of getting a quantum version of EasyCrypt.)
Abstract: A lecture on problems and solutions related to quantum random oracles.
Abstract: A lecture on problems and solutions related to quantum rewinding.
Abstract: In recent years, the verification of cryptographic schemes on the computational level (i.e., without symbolic abstractions) has seen great progress. For example, various state-of-the-art cryptographic schemes were analyzed using the EasyCrypt tool using a probabilistic relational Hoare logic (pRHL). However, existing tools and logics are unsuited for analysis of quantum cryptographic protocols – be it protocols using quantum mechanics, or protocols secure against quantum adversaries. In this talk, we explain why pRHL is not sound for quantum cryptography, and show how to lift the ideas from pRHL to the quantum setting. (With the long-term goal of getting a quantum version of EasyCrypt.)
Abstract: We present a new definition of computationally binding commitment schemes in the quantum setting, which we call “collapse-binding”. The definition applies to string commitments, composes in parallel, and works well with rewinding-based proofs. We give simple constructions of collapse-binding commitments in the random oracle model, giving evidence that they can be realized from hash functions like SHA-3. We evidence the usefulness of our definition by constructing three-round statistical zero-knowledge quantum arguments of knowledge for all NP languages.
Abstract: We present a construction for non-interactive zero-knowledge proofs of knowledge in the random oracle model from general sigma-protocols. Our construction is secure against quantum adversaries. Prior constructions (by Fiat-Shamir and by Fischlin) are only known to be secure against classical adversaries, and Ambainis, Rosmanis, Unruh (FOCS 2014) gave evidence that those constructions might not be secure against quantum adversaries in general. To prove security of our constructions, we additionally develop new techniques for adaptively programming the quantum random oracle.
Abstract: Zero-knowledge proofs are a powerful tool in cryptography, allowing to prove the truth of a fact without revealing anything else. However, in their most basic form, ZK proofs are interactive, which makes them difficult to use in practice. Efficient transformations exist that make a ZK proof non-interactive (Fiat-Shamir, in the random-oracle model). But those fail in the quantum setting. We explain the difficulties in the quantum setting, show how to circumvent them, and close with a quantum query complexity problem whose solution would lead to a much simpler protocol.
Abstract: Formal verification of cryptographic protocols has been an active research area for several decades, mostly in idealized symbolic models, but more recently also with respect to actual computationally bounded attackers. However, verification is always restricted to classical protocols and classical adversaries (to the best of our knowledge). Yet, if quantum computers arrive some day, we need cryptography that is secure against them. In this talk, we discuss the question what challenges we face if we wish to take into account quantum adversaries and/or quan- tum protocols. We particularly focus on the verification of cryptography against computationally bounded attackers.
The talk does not require any prior knowledge in quantum cryptography. We will discuss the nature, relevance and threats of quantum cryptography in the talk.
Abstract: We present a construction for non-interactive zero-knowledge proofs of knowledge in the random oracle model from general sigma-protocols. Our construction is secure against quantum adversaries. Prior constructions (by Fiat-Shamir and by Fischlin) are only known to be secure against classical adversaries, and Ambainis, Rosmanis, Unruh (FOCS 2014) gave evidence that those constructions might not be secure against quantum adversaries in general. To prove security of our constructions, we additionally develop new techniques for adaptively programming the quantum random oracle.
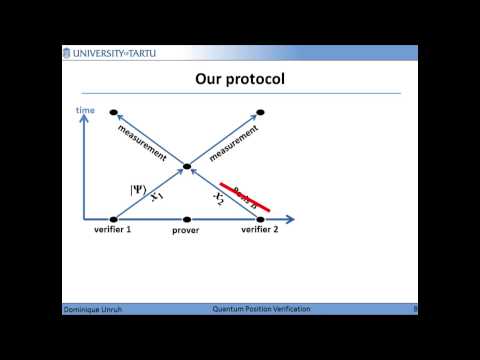
Abstract: We present a quantum position verification scheme in the random oracle model. In contrast to prior work, our scheme does not require bounded storage/retrieval/entanglement assumptions. We also give an efficient position-based authentication protocol. This enables secret and authenticated communication with an entity that is only identified by its position in space.
Abstract: Quantum zero-knowledge proofs and quantum proofs of knowledge are inherently difficult to analyze because their security analysis uses rewinding. Certain cases of quantum rewinding are handled by the results by Watrous (SIAM J Comput, 2009) and Unruh (Eurocrypt 2012), yet in general the problem remains elusive. We show that this is not only due to a lack of proof techniques: relative to an oracle, we show that classically secure proofs and proofs of knowledge are insecure in the quantum setting.
More specifically, sigma-protocols, the Fiat-Shamir construction, and Fischlin's proof system are quantum insecure under assumptions that are sufficient for classical security. Additionally, we show that for similar reasons, computationally binding commitments provide almost no security guarantees in a quantum setting.
To show these results, we develop the "pick-one trick", a general technique that allows an adversary to find one value satisfying a given predicate, but not two.
Abstract: We present a quantum position verification scheme in the random oracle model. In contrast to prior work, our scheme does not require bounded storage/retrieval/entanglement assumptions. We also give an efficient position-based authentication protocol. This enables secret and authenticated communication with an entity that is only identified by its position in space.
Abstract: Quantum zero-knowledge proofs and quantum proofs of knowledge are inherently difficult to analyze because their security analysis uses rewinding. Certain cases of quantum rewinding are handled by the results by Watrous (SIAM J Comput, 2009) and Unruh (Eurocrypt 2012), yet in general the problem remains elusive. We show that this is not only due to a lack of proof techniques: relative to an oracle, we show that classically secure proofs and proofs of knowledge are insecure in the quantum setting.
More specifically, sigma-protocols, the Fiat-Shamir construction, and Fischlin's proof system are quantum insecure under assumptions that are sufficient for classical security. Additionally, we show that for similar reasons, computationally binding commitments provide almost no security guarantees in a quantum setting.
Abstract: We present a quantum position verification scheme in the random oracle model. In contrast to prior work, our scheme does not require bounded storage/retrieval/entanglement assumptions. We also give an efficient position-based authentication protocol. This enables secret and authenticated communication with an entity that is only identified by its position in space.