Sirge võrrand ristkoordinaatides on $y=ax+b$, kus $a$ on sirge tõus ja $b$ on algordinaat. Koondame katsepunktid vektoreisse x ja y. Katsepunkte läbiva optimaalse sirge (ehk 1-järku polünoomi) parameetrid leiame nii:

a, b = np.polyfit(x, y, 1)

Alternatiivselt võib kasutada funktsiooni linregress moodulist scipy.stats, mis tagastab muuhulgas ka tõusu standardhälbe:

from scipy.stats import linregress

a, b, _, _, ua = linregress(x, y)

Algordinaadi standardmääramatus avaldub $u_A(a)$ kaudu: $$u_A(b)=u_A(a)\sqrt{\frac{\sum x_i^2}{n}},$$ kus $n$ on andmepunktide arv. Ruutjuure all on lihtsalt kõigi $x_i^2$ aritmeetiline keskmine, seega

ub = ua * sqrt(np.mean(x**2))

Kui lineaarne seos kehtib vaid teatud vahemikus (näiteks alates $x=0,\!5$ kuni $x=2,\!2$), siis tuleb esmalt vastavad andmepunktid algmassiividest välja lõigata:

õiged = (x > 0.5) & (x < 2.2)  # tõeväärtuste massiiv
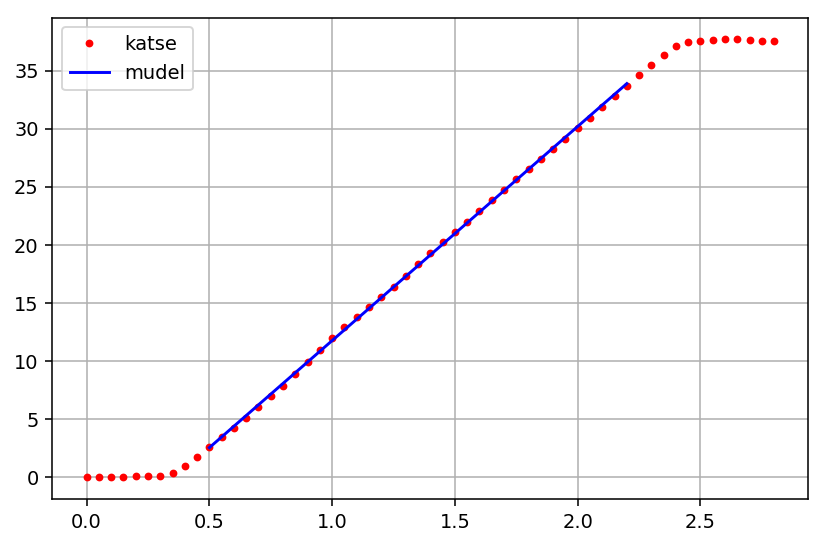
a, b = np.polyfit(x[õiged], y[õiged], 1)

Soovitatav on ka graafiliselt demonstreerida teoreetilise kõvera klappimist katsepunktidega:

plot(x, y, 'r.', label='katse')
plot(x, a * x + b, 'b-', label='mudel')
grid()
legend()
show()

Sisukord