Mittelineaarse funktsiooni sobitab (vähimruutude mõttes) läbi andmepunktide scipy.optimize.curve_fit. Esmalt tuleb defineerida lähendusfunktsioon ise. Selle esimeseks argumendiks on sõltumatu muutuja ja ülejäänud argumendid on vabad parameetrid. Lähendusfunktsioon peab olema vektoriseeritud kujul, st tuleb kasutada moodulist numpy (ja mitte math) pärinevaid matemaatikafunktsioone. Üldjuhul vajatakse ka parameetrite alglähendeid. Kõik need andmed (koos katsepunktidega) edastatakse funktsioonile curve_fit, mis tagastab parameetrite optimaalsed väärtused vektorina.

Järgmises näites sobitatakse katseandmetega funktsioon $y=ae^{-bx} + c$, kus vabad parameetrid on $a$, $b$ ja $c$.

from scipy.optimize import curve_fit

# mõõdetud
x = np.array((0.00, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50))
y = np.array((352.55, 331.85, 319.05, 312.05, 306.55, 303.55, 301.35, 299.95, 298.85, 298.25, 297.75))

# mudelfunktsioon
f = lambda x, a, b, c: a * np.exp(-b * x) + c

# alglähend
a, b, c = 60, 10, 290

# optimeerimine
(a, b, c), cov = curve_fit(f, x, y, (a, b, c))

# tulemused
print(f'Parameetrid: a = {a:.2f}, b = {b:.3f}, c = {c:.2f}')

# teoreetiline kõver
u = np.linspace(0, 0.55, 100)
v = f(u, a, b, c)

#graafik
plot(x, y, 'ro', label='katse')
plot(u, v, 'b-', label='mudel')
grid()
legend()
show()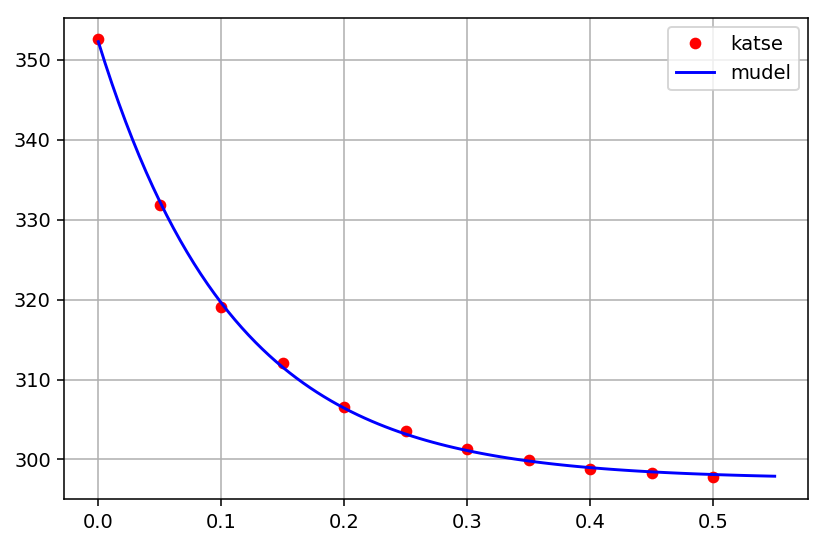

Piisavalt lihtsa mudelfunktsiooni korral saab parameetrite alglähendid hinnata katseandmete graafikult. Antud näites $a$ on signaali maksimaalne muut (amplituud), $b$ pöördväärtus on karakteerne aeg või distants, mille vältel signaali muutus aset leiab, ja $c$ väljendab funktsiooni asümptootilist väärtust piiril $x\to\infty$. Keerulisema funktsiooni korral võib alglähendid leida katse-eksituse meetodil, jälgides teoreetilise kõvera kattuvust katsepunktidega. Selleks tuleb eelnevas koodis funktsiooni curve_fit sisaldav rida (ajutiselt) välja kommenteerida.

Soovitav on lisada andmepunktidele ka vearistid ja veenduda, et modelleeritud kõver piirvea/määramatuse piires läbib kõiki katsepunkte:

plot(x, y, 'r.', label='katse')
errorbar(x, y, yerr=1.2, fmt='none', ecolor='r', elinewidth=0.75, capsize=2)
plot(ξ, ψ, 'b-', label='mudel')
grid()
legend()
tight_layout()
show()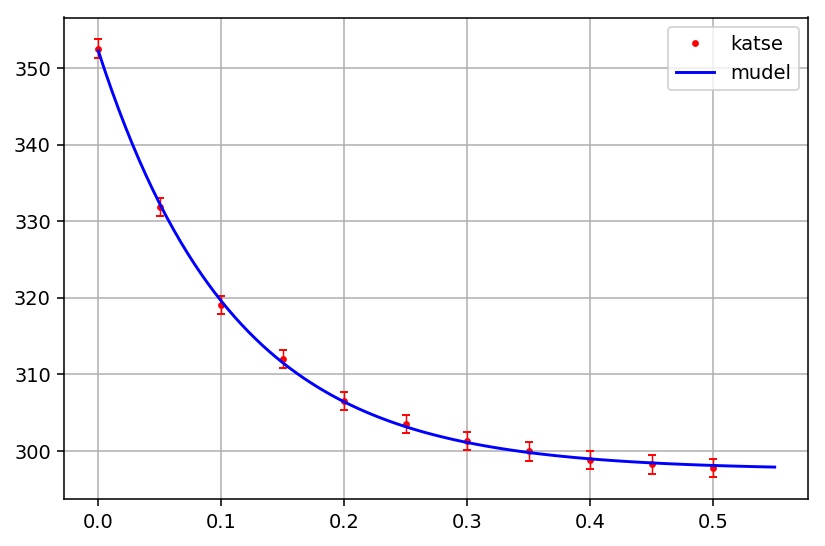

Lisaks optimeeritud parameetritele tagastab curve_fit ka kovariatsioonimaatriksi (cov), mille kaudu saab vajadusel parameetrite standardmääramatused:

ua, ub, uc = np.sqrt(np.diag(cov))
print(f'Määramatused: u(a) = {ua:.2f}, u(b) = {ub:.3f}, u(c) = {uc:.2f}')

Sisukord