Vaatleme näitena ühtlase kiirendusega liikumise üldvalemit:
$$x(t)=x_0+v_0t+\frac{1}{2}at^2.$$See sisaldab sõltumatut muutujat (aega $t$) esimeses ja teises astmes.
Seda laadi üldist funktsiooni nimetatakse polünoomiks:
$$x(t)=p_0t^n+p_1t^{n-1}+\ldots+p_{n-1}t+p_n,$$
kus $p_0\ldots p_n$ on konstandid (polünoomi kordajad). Sellise funktsiooni
sobitab läbi etteantud andmepunktide numpy.polyfit,
mis tagastab vektorina polünoomi kordajad:
p = np.polyfit(aeg, koordinaat, 2)
algkiirus = p[1]
kiirendus = 2 * p[0]Siin funktsiooni polyfit viimane parameeter on nõutud
polünoomi järk $n$, mis antud juhul on 2.
Kui selline mudel kehtib katseandmete jaoks vaid piiratud ajavahemikus (näiteks alates $t=0,\!5$ kuni $t=2,\!2$), siis tuleb esmalt vastavad andmepunktid algmassiividest välja filtreerida:
õiged = (aeg > 0.5) & (aeg < 2.2) # tõeväärtuste massiiv
p = np.polyfit(aeg[õiged], koordinaat[õiged], 2)Soovitatav on ka graafiliselt demonstreerida teoreetilise kõvera
klappimist katsepunktidega. Teades polünoomi kordajaid, saab
polünoomi väärtuse teada funktsiooniga numpy.polyval:
t = np.linspace(0.5, 2.2, 100)
x = np.polyval(p, t)
plot(aeg, koordinaat, 'r-', label='katse')
plot(t, x, 'b-', label='mudel')
grid()
legend()
show()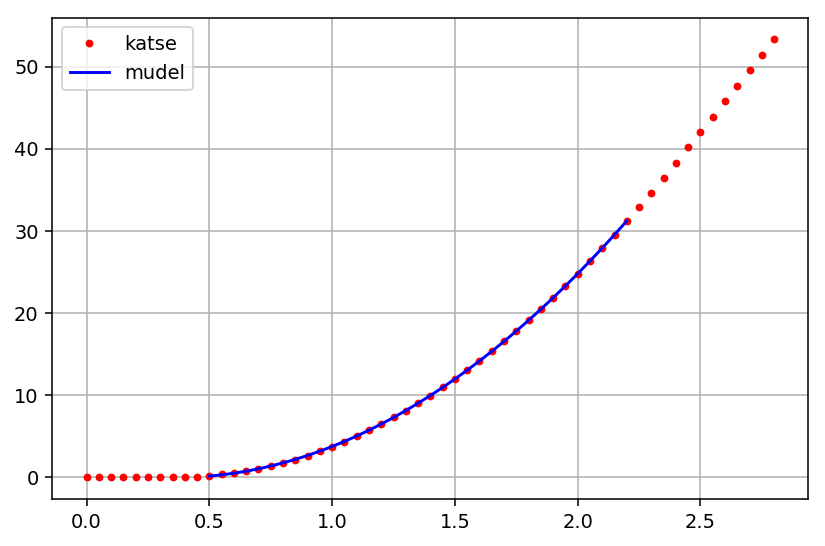
Kui anda funktsioonile polyfit valikuline parameeter
cov=True, tagastatakse ka leitud kordajate kovariatsioonimaatriks,
mille diagonaalelementide kaudu saab kordajate standardmääramatused:
(a, b, c), cov = np.polyfit(aeg, koordinaat, 2, cov=True)
ua, ub, uc = np.sqrt(np.diag(cov))