Kuna mistahes eksperimentaalne sõltuvus võetakse paratamatult üles lõpliku sammuga, võib tekkida vajadus mõõdetava suuruse väärtuse hindamiseks katsepunktide vahel. Probleem esineb näiteks juhul kui erinevate andurite näidud registreeritakse veidi erinevatel ajahetkedel või kui tuleb andmetöötluses kasutada olemasolevaid, tabuleeritud andmeid (artiklist, käsiraamatust, vms). Kui andmeseeriat kirjeldav teoreetiline sõltuvus on teada ja piisavalt lihtne, saab kasutada funktsiooni sobitamist vähimruutude meetodil. Vastasel korral, ühtlasi eeldades et katsepunktide määramatus on piisavalt väike, on õigustatud interpoleerimine, st konstrueeritakse võimalikult sile kõver, mis läbib täpselt kõiki katsepunkte, aga millel teoreetilist põhjendust ei ole.
Lihtsaim lahendus on ühendada järjestikused katsepunktid sirgega. Sellise nn
lineaarse interpolatsiooni teostab numpy.interp. Kui andmepunktide
koordinaadid on vektorites x ja y, siis
numpy.interp(ξ, x, y) annab lineaarselt interpoleeritud väärtuse kohal
ξ.
plot(x, y, 'ro', label='andmed', zorder=3)
ξ = np.linspace(0, 9, 100) # interpoleeritud kõver peenema sammuga
plot(ξ, np.interp(ξ, x, y), 'b-', label='interpoleeritud')
# graafikul rohelise värviga joonestatud elemendid
ξ = 5.5
η = np.interp(ξ, x, y)
plot(ξ, η, 'g.')
axvline(ξ, color='g', ls='--')
axhline(η, color='g', ls='--')
text(ξ, 0.13, 'ξ', ha='center', va='top', color='g')
text(-0.55, η, 'η', ha='right', va='center', color='g')
grid()
legend()
show()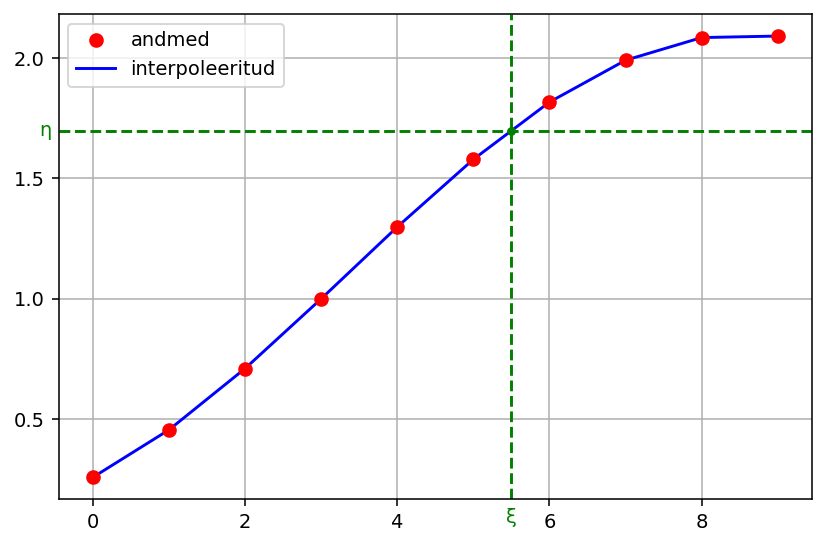
Üldisem võte on ühendada järjestikused katsepunktid polünoomidega, nii et
moodustuks võimalikult sile kõver, mida nimetatakse splainiks. Seda teostab
scipy.interpolate.interp1d. Lisaparameetriga kind
määratakse interpolatsioonimeetod, näiteks 'linear' (vaikimisi),
'quadratic', 'cubic'.
from scipy.interpolate import interp1d
f1 = interp1d(x, y) # vaikimisi lineaarne interpolatsioon
f2 = interp1d(x, y, kind='cubic')
ξ = np.linspace(0, 9, 100) # interpoleeritud kõver peenema sammuga
plot(x, y, 'ro', label='andmed', zorder=3)
plot(ξ, f1(ξ), 'b--', label='lineaarne')
plot(ξ, f2(ξ), 'b-', label='kuupsplain')
grid()
legend()
show()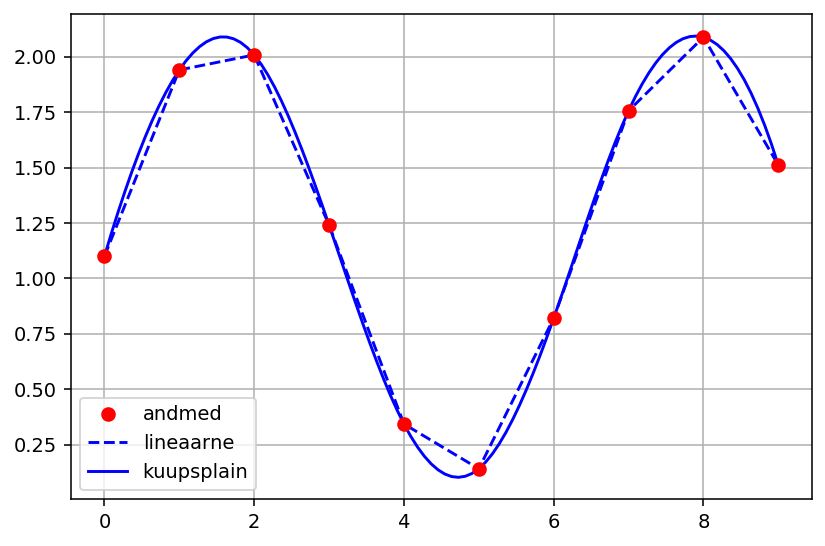
On ilmne, et sedavõrd hõredalt paiknevate andmepunktide korral lineaarne interpolatsioon annab ebaloomuliku ja ebatäpse tulemuse.