LTFY.01.004 Füüsika praktikum I - mehaanika ja soojusõpetus
- Liikumine kaldteel
- Kummipaela elastsus
- Inertsimomendi mõõtmine pöördliikumise anduriga
- Veeremine kaldpinnal
- Katsed kalorimeetriga
Liikumine kaldteel
Seni kuni vanker jätkab liikumist ühes suunas (ja lugedes hõõrdeteguri kiirusest sõltumatuks), püsib vankri kiirendus konstantne. Seega liikumisvõrrand on $x=x_0+v_0t+\frac{1}{2}at^2$ ja vastavat osa trajektoorist võib sobitada parabooliga. Kui aga liikumise kestel suund muutub, siis ka hõõrdejõud muudab märki. Seega vankri kiirendus $a=\frac{1}{m}(F_\text{g}\pm F_\text{h})$, kus $F_\text{g}$ on raskusjõu komponent piki kaldpinda ja $F_\text{h}$ on hõõrdejõud (kõik absoluutväärtused). Kui kombineerida liikumist mõlemas suunas, saab $F_\text{h}$ välja taandada.
Kummipaela elastsus
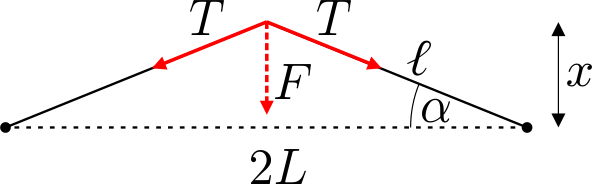Pingule tõmmatud kummipaelale mõjutakse ristisihilise jõuga $F$ ja uuritakse
selle sõltuvust läbivajumisest $x$. Olgu
kummipaela jäikustegur $k$, kinnituspunktide vahekaugus $2L$, kummipaela ühe
poole pikkus $\ell$ ja vastav algpikkus (venimata olekus) $\ell_0$. Hooke'i
seadusest saame pinge
kummipaelas, $T=k(\ell-\ell_0)$, kus omakorda Pythagorase teoreemist
$\ell=\sqrt{L^2+x^2}$. Viimaks, mõõdetav jõud $F=2T\sin\alpha=2Tx/\ell$.
Seega tekib küllalt keeruline mittelineaarne seos $F$ ja $x$ vahel. Tasub ka arvestada, et
asendianduri nullasend ei pruugi olla täpselt sama mis $x=0$.
Inertsimomendi mõõtmine pöördliikumise anduriga
Kommentaariks,
Halliday õpiku lahenduses defineeritakse süsteemi läbivalt positiivse liikumise suund,
seetõttu mõned jõud ja kiirendused tulevad negatiivsed. Samas on antud lihtsas süsteemis
kõigi jõudude ja liikumiste suunad ette teada, seetõttu järgnevas
eeldame, et kõik suurused on positiivsed (v.a. aeglustuv liikumine, mille
korral kiirendused on negatiivsed). Lisaks võtame arvesse ka hõõrdumist.
Tegemist on seotud kehade liikumisega. Selliste probleemide lahendamisel tuleb koostada hulk võrrandeid, lähtudes järgmistest põhimõtetest:
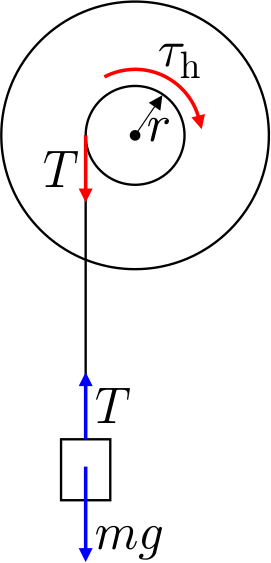
- Eraldi iga keha jaoks teha kindlaks kõik sellele kehale mõjuvad jõud ja panna vastavalt kirja Newtoni II seadus (või selle analoog pöördliikumise jaoks). Näiteks joonisel on erinevate värvidega näidatud jõud, mis mõjuvad kettale (punased nooled) ja koormisele (sinised nooled).
- Pöörlevale süsteemile mõjuv hõõrdejõud on hajutatud ehk me ei saa täpselt näidata selle suurust, suunda ega rakenduspunkti. Järelikult sellist hõõrdumist tuleb iseloomustada jõumomendiga ($\tau_\text{h}$).
- Massitule kehale mõjuvad jõud peavad olema tasakaalus (muidu keha hakkaks liikuma lõpmatu kiirendusega). Seega, niidi otstele mõjuvad tõmbejõud peavad olema võrdvastassuunalised. Teiste sõnadega, pinge niidis ($T$) on kõikjal sama.
- Tulenevalt Newtoni III seadusest, mõned jõud on võrdvastassuunalised. Näiteks, nagu joonisel näha, jõud, millega koormis sikutab (niidi vahendusel) ketast, on suuruselt võrdne jõuga, millega ketas tõmbab koormist.
- Kuna kehade liikumine on seotud (niit ei veni), siis esineb kinemaatiline (geomeetriline) seos vastavate liikumiste vahel (antud juhul koormise lineaarkiirenduse $a$ ja ketta nurkkiirenduse $\alpha$ vahel).
Kõike seda arvestades saame võrrandisüsteemi: $$\begin{cases} ma=mg - T\\ I\alpha=Tr-\tau_\text{h}\\ a=\alpha r \end{cases}$$ Siit võime elimineerida näiteks $T$ ja $a$ (mis pakuvad kõige vähem huvi): $$I\alpha=mr(g-\alpha r)-\tau_\text{h}.$$ Seda üldlahendit tuleb kohaldada erinevatele katsetele ja tulemusi kombineerida. Põhikatses ilmselt $I=I_\text{keha}+I_\text{andur}$. Seevastu katses tühja anduriga $I=I_\text{andur}$, ja kuna sel juhul pöörleva süsteemi mass on samuti hulga väiksem, siis loeme $\tau_\text{h}\approx 0$. Mõeldav on ka teha katseid mitme erineva koormisega, või ka ilma koormiseta (sel juhul $mg=0$ ja jääb vaid hõõrdumine, nii et liikumine on aeglustuv ehk $\alpha < 0$). Niimoodi mitut katset kombineerides tekib üldiselt veel üks võrrandisüsteem, näiteks: $$\begin{cases} (I_\text{keha}+I_\text{andur})\alpha_1=mr(g-\alpha_1 r)-\tau_\text{h}\\ (I_\text{keha}+I_\text{andur})\alpha_2=-\tau_\text{h}\\ I_\text{andur}\alpha_3=mr(g-\alpha_3 r) \end{cases}$$ Siit saab juba avaldada huvipakkuvad suurused ($I_\text{keha}$, $I_\text{andur}$, $\tau_\text{h}$) erinevate otseselt mõõdetud suuruste ($m$, $r$, $\alpha_1$, $\alpha_2$, $\alpha_3$) kaudu. Kuivõrd valemid tulevad juba päris keerulised, võib kontrolliks piirduda põhikatsega, ignoreerides kõiki sekundaarseid efekte ($I_\text{andur}\approx 0$, $\tau_\text{h}\approx 0$).
On mõeldav, et mõne pöörleva keha korral on ka õhutakistus oluline, kusjuures see sõltub veel pöörlemiskiirusest. Viimasel juhul peab see avalduma selles, et kiirendus ei ole enam konstant.
Veeremine kaldpinnal
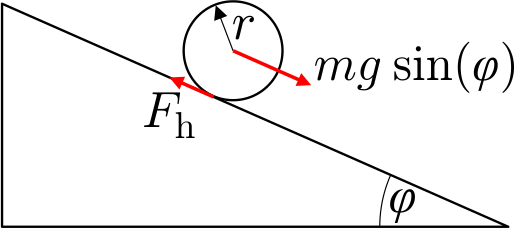See olukord on
füüsikaliselt ja matemaatiliselt sarnane eelmise ülesandega. Siin on küll
vaid üks liikuv keha, aga see osaleb korraga kahes liikumises (kulgemine ja pöörlemine).
Kui libisemist ei toimu, siis need kaks liikumist on jällegi kinemaatiliselt
seotud. Joonisel on kujutatud vaid need jõud, mis mõjuvad kuulile kaldpinna
sihis (ristisihis mõjuvad jõud tasakaalustavad üksteist). $F_\text{h}$ on
hõõrdejõud, mis mõjub kuuli ja kaldpinna vahel. Seega võrrandisüsteem tuleb järgmine:
$$\begin{cases}
ma=mg\sin(\varphi) - F_\text{h}\\
I\alpha=F_\text{h}r\\
a=\alpha r
\end{cases}$$
Katsed kalorimeetriga
Omapead jäetuna jahtub kuumutatud objekt (nt kuuma veega täidetud kalorimeeter) mitmesuguste soojusülekannete tõttu ümbritsevasse keskkonda (soojusjuhtivus, konvektsioon, jm). Lihtsaim mudel selle kirjeldamiseks on Newtoni seadus, kus eeldatakse, et soojusvoog on võrdeline objekti ja keskkonna temperatuuride vahega. Vastav võrdetegur iseloomustabki süsteemi soojuslekki. Kui lugeda see ja muud süsteemi parameetrid temperatuurist sõltumatuks, saame, et objekti temperatuur ajas eksponentsiaalselt läheneb keskkonna temperatuurile. See mudel on mõistagi seda täpsem, mida väiksem on vaadeldav temperatuurivahemik.
Erisoojuse määramise eksperimendis kasutatakse kahte termomeetrit. Termomeetri üksikmõõtmise piirviga on küllaltki suur, kuni 0,5 °C. Lisaks, termomeetrite näidud ei pruugi ühtida. Samas tasub tähele panna, et:
- Termomeetrite näitude erinevus on praktiliselt konstant (ei sõltu temperatuurist).
- Selles katses on sisuliselt tähtis vaid temperatuurivahede või -muutude (mitte absoluutse temperatuuri) mõõtmine.
Seega, kui termomeetrite näitude erinevus parandina arvesse võtta, võiks temperatuuri registreerimisel saavutada täpsuse, mis läheneb lahutusvõimele (0,1 °C).
Juhendi koostas Valter Kiisk
Viimati muudetud 29.04.2024