Sissejuhatus
Sisukord
Matemaatiliste arvutuste teostamiseks PC laadsel arvutil on hulk
võimalusi. Ühe tehte kaupa saab opereerida
kalkulaatori-tüüpi rakendusega. Pikemaid rehkendusi (sh parameetrite/vahetulemuste
säilitamine muutujates, andmevahetus failidega jne) saab sooritada tüüpilises
programmeerimiskeskkonnas. Seejuures kompileeritavad keeled (Pascal,
C, Fortran
jne) on ka ülimalt kiired (selleks peab olema muidugi tõeliselt arvutusmahukas
ülesanne, et seda kiirust realiseerida). Interpreteeritavad keeled on jälle
lihtsamad kasutada. Näiteks
JavaScript
ei nõua mitte midagi peale veebilehitseja olemasolu. Paljudel juhtudel on
asjakohane hoopis mõni tabelarvutusprogramm (MS Excel
vms). Nimetatud süsteemidel on siiski vähemalt kaks suurt puudust: (1) matemaatilised
avaldised tuleb sisestada primitiivsel (lihtteksti) kujul ja (2) saadaval
on vaid elementaarmatemaatika vahendid (liitmine, lahutamine, astendamine,
juurimine, jne). Siin tulevadki mängu spetsiaalsed programmipaketid teadus-
ja insenertehniliste arvutuste jaoks, mille tuntud kommertsiaalsed esindajad
on
Maple,
Matlab,
Mathematica
ja Mathcad.
Nende programmide standardvarustuses on juba arvutused maatriksite ja kompleksarvudega,
algebraliste ja diferentsiaalvõrrandite lahendamine, tuletised ja integraalid,
erifunktsioonid, sümbolarvutus, piiramatu arvutustäpsus jpm.
Mathcad on tänu oma intuitiivsele ja interaktiivsele kasutajaliidesele üks kergemini omandatavaid arvutuspakette. Matemaatilisi avaldisi saab sisestada ligilähedaselt loomulikul kujul nagu trükitud tekstides. Selle tõttu eriti tabelarvutussüsteemidega võrreldes on Mathcad'i dokumendis hulga lihtsam jälgida arvutuste käiku. Võrdleme näiteks ruutvõrrandi lahendivalemit erinevates süsteemides:
| Maple | x=(-b+sqrt(b^2-4*a*c))/(2*a); |
|---|---|
| Pascal | x:=(-b+sqrt(b*b-4*a*c))/(2*a); |
| Excel | =(-B1+SQRT(B1*B1-4*A1*C1))/(2*A1) |
| Mathcad |
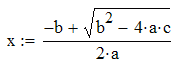 |
| Tavaline trükitud tekst | \[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\] |
Tõsi küll, nüüdseks juba pikemat aega on ka mõned muud süsteemid (nt Maple ja Mathematica) lubanud spetsiaalses režiimis ilusti kujundatud matemaatiliste avaldiste sisestamist, kuid see ei ole siiski loomupärane osa nende kasutajaliidesest.
Kõik Mathcad'i dokumendis ehk töölehel sisalduv paikneb ristkülikulaadsete piirkondade e. plokkidena. Põhilised on arvutus-, teksti- ja graafikupiirkonnad. Oluline erinevus muude matemaatikapakettidega seisneb selles, et plokke võib paigutada meelevaldselt kogu töölehe ulatuses (nagu pliiatsiga paberile kirjutades) kusjuures plokkide paigutus määrab ka loomulikul viisil arvutuste järjekorra: vasakult paremale ning ülevalt alla. Iga muutuja või funktsiooni definitsioon mõjutab vaid seda töölehe piirkonda, mis asub temast paremal või allpool kuni kohani kus sama identifikaator üle defineeritakse või kuni jõutakse töölehe lõppu. Juhul kui Tools → Calculate → Automatic Calculation on sisse lülitatud, on arvutusprotsess "elav", st iga avaldise või graafiku uuendamine toimub automaatselt, niipea kui sellele eelnevas arvutusahelas on modifitseeritud muutujate või funktsioonide definitsioone, millest see piirkond sõltub. Nii terve töölehe kui ka aktiivse piirkonna uuestiarvutamise saab vajadusel käivitada käsitsi (vastavalt Tools → Calculate → Calculate Worksheet või Calculate Now F9), kuid see võib arvutustulemusi mõjutada vaid juhul kui loetakse andmefailist uued andmed või kui arvutusahelas sisaldub juhuslike arvude generaator; üldjuhul piisab arvutuste automaatsest uuendamisest.
Mathcad'i lihtsuse hind on mõningane kaotus arvutuskiiruses ning programmikoodi paindlikkuses ja hallatavuses. Need probleemid ilmnevad reeglina alles mahukamate ülesannete lahendamisel. Mahukate numbriliste (eriti maatrikskujul) arvutuste tegemisel on üldiselt parim Matlab, arvutialgebra jaoks aga Maple või Mathematica. Kõigile viimatimainituile leidub ka hulk vabavaralisi alternatiive (Scilab, Maxima, Sage, IPython jpt). Ainus Mathcad'i sarnane vabavara paistab olema SMath Studio. Mathcad'i tegijatelt on vabalt saadaval piiratud võimalustega versioon Mathcad Express. Ühed jõudlustesti tulemused on raporteeritud viites .
Lisaks graafikute vormistamisele on Origin'i tüüpi programmides mõnevõrra mugavam sooritada mõningaid keerukaid andmetöötlusoperatsioone, mis eeldavad graafilist tagasisidet, näiteks funktsioonide sobitamine katseandmetega, andmete silumine või Fourier' analüüs. Võrreldes aga Mathcad'i taoliste programmidega on nende tegevuste omavaheline seostamine ja automatiseerimine komplitseeritum.Mathcad on eelkõige arvutusvahend ja vähemalt senised versioonid ei võimalda esitlus- või publitseerimiskvaliteediga graafikute vormistamist. Viimaste saamiseks tuleb kasutada spetsiaalseid programme nagu Origin, SigmaPlot ja IGOR Pro (ka Exceli graafikavahendid on paremad). Andmefailide importimise/eksportimise teel saab organiseerida vajaliku andmevahetuse. Samal põhjusel on ka Mathcad'i tekstitöötlusvahendid võrdlemisi primitiivsed ja sobilikud eelkõige arvutuskäigu kommenteerimiseks.
Redigeerimine
SisukordKasutajaliidese üldiselt ülesehituselt on Mathcad klassikaline dokumendipõhine Windows'i rakendus. Dokumendiks on virtuaalne paber ehk tööleht, millel olevaid arvutus- ja tekstiplokke saab toimetada, vormindada, lohistada, kopeerida jne. Dokumendi toimetamise lõpptulemina sünnib teatavas üsna intuitiivses koodis kirja pandud arvutusprogramm, mis peab lahendama püstitatud arvutus- või andmetöötlusülesande. Tüüpiline tööleht algab lähteandmete sisestamisega (käsitsi või andmefailist) ja lõpeb arvutustulemuste väljastamisega arvulisel, graafilisel või faili kujul. Saab toimetada paralleelselt mitmes avatud dokumendis (multiple document interface). Nagu kõigi sellise ülesehitusega rakenduste korral, tasub produktiivse töö huvides meeles pidada standardsete käskude kiirkorraldused nagu Ctrl+S (salvesta dokument), Ctrl+X (lõika puhvrisse), Ctrl+C (kopeeri puhvrisse), Ctrl+V (kleebi puhvrist), Ctrl+Tab (lülitu järgmisele dokumendile), Ctrl+Z (võta tagasi) jne. Ctrl+Z korduva rakendamisega saab tagasi võtta rohkem kui ühe toimingu (alates Mathcad 11).
 Matemaatiliste
operaatorite, graafikute ja sümbolite sisestamiseks on rida temaatilisi
tööriistapalette. Neid saab sisse-välja lülitada paletilt
Math. Ajapikku tuleks meelde jätta põhiliste
operatsioonide kiirkorraldused (mille saab teada kui hoida hiirekursorit
mõned hetked vastava ikooni kohal), sest hiirega nupukeste ja menüükäskude
tagaajamine muudab töötegemise ebaproduktiivseks.
Matemaatiliste
operaatorite, graafikute ja sümbolite sisestamiseks on rida temaatilisi
tööriistapalette. Neid saab sisse-välja lülitada paletilt
Math. Ajapikku tuleks meelde jätta põhiliste
operatsioonide kiirkorraldused (mille saab teada kui hoida hiirekursorit
mõned hetked vastava ikooni kohal), sest hiirega nupukeste ja menüükäskude
tagaajamine muudab töötegemise ebaproduktiivseks.
Arvutuspiirkonna tekitamiseks tuleb kursor (punane ristike) liigutada soovitud kohta töölehel (hiirega klikkides või nooleklahvidega) ja asuda valemit sisse toksima. Redigeerimise klahvid on võrdlemisi intuitiivsed: * tekitab korrutise, / tekitab murru, ^ tekitab astendaja, \ tekitab ruutjuure jne, sisestuskoha muutmine toimub nooleklahvidega (mängida tasub ka tühiku- ja Insert-klahviga). Operaatori (näiteks korrutusmärgi) sisestamisel tekib selle kõrvale automaatselt musta kastikese kujuline lünk (placeholder), mis näitab kuhu järgmine argument tuleb kirjutada. Sulgavaldisi tekitatakse ( ja ) klahvidega (klahv ' tekitab mõlemad sulud korraga) ja Mathcad otsustab ise kas kuvada ümar- või kandilised sulud. Vaatleme näitena ruutvõrrandi lahendivalemi sisestamise protsessi:
| Klahvivajutused | Tulemus |
|---|---|
| (algseis) |  |
| x |  |
| : |  |
| - |  |
| b |  |
| + |  |
| \ |  |
| b ^ 2 | 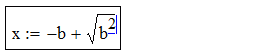 |
| Space | 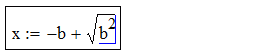 |
| - | 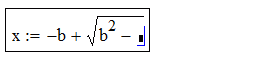 |
| 4 * | 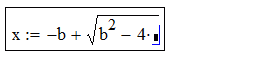 |
| a * c | 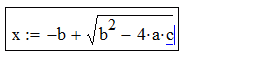 |
| Space Space Space Space Space | 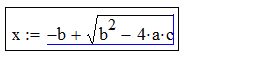 |
| / | 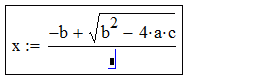 |
| 2 * a | 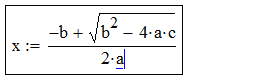 |
| = | 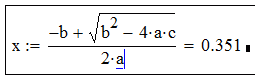 |
Elementide lisamine avaldise sisestamisel ei pea toimuma tingimata "õiges" järjekorras. Näiteks äsjase näite saab realiseerida ka järgmiselt:
| Klahvivajutused | Tulemus |
|---|---|
| (algseis) |  |
| b ^ 2 Space - 4 * a * c |  |
| Space Space Space |  |
| \ |  |
| Insert |  |
| + |  |
| - b | 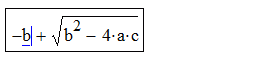 |
| Space Space / 2 * a |  |
| Space Space Insert |  |
| : | 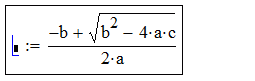 |
| x | 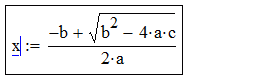 |
| = | 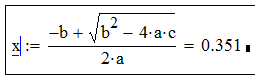 |
Muutujanimede valikul ei ole Mathcad piiratud traditsiooniliste programmeerimiskeelte reeglitega vaid lubab kasutada ka kreeka tähti, alaindekseid, täpitähti ja paljusid erisümboleid (ainus piirang on, et identifikaator ei tohi alata numbriga). Kiireim võte kreeka tähtede saamiseks on sisestada esmalt vastav ladina täht ja vajutada seejärel Ctrl+G. Alaindeksi saab tekitada lisades muutujanimesse punkti. Selleks et kõikvõimalikke erisümboleid (näiteks <, +, $ jne) muutujanime koosseisu kaasata, tuleb muutujanime redigeerimisel siseneda klahvivajutusega Ctrl+Shift+K ajutiselt spetsiaalsesse tekstirežiimi, sisestada vajalikud sümbolid ja seejärel väljuda tavalisse režiimi sama klahvikombinatsiooniga. Ilma mainitud erirežiimita saab muutujanimesse sisestada priimi ' (Ctrl+F7), protsendimärgi % ja allkriipsu _. Näiteks valemi \(F_\text{hõõrde}=\mu mg\) sisestus näeks välja järgmine:
| Klahvivajutused | Tulemus |
|---|---|
| (algseis) |  |
| F |  |
| . h õ õ r d e | 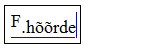 |
| : m | 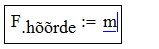 |
| Ctrl+G | 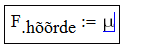 |
| * m * g | 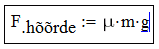 |
| Enter | 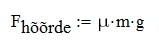 |
Tekstipiirkonna tekitamise kiirkorralduseks on jutumärgid (või toksida esimene sõna tekstist ja vajutada tühikuklahvi). Elegantsema väljanägemise huvides saab matemaatikaploki asetada ka tekstipiirkonna sisse kasutades käsku Insert → Math Region (Ctrl+Shift+A) või siis lõika-kleebi meetodil. Nii teksti kui ka matemaatiliste sümbolite fonti saab muuta, olemas on ka laadide (styles) kasutamise võimalus. Tekstipiirkonna laade kontrollitakse dialoogis Format → Style, matemaatiliste sümbolite laade aga dialoogis Format → Equation. Harilikult tarvitatakse vaid kahte matemaatikalaadi: Variables (muutuja- ja funktsioonitähised) ja Constants (arvud). Muude laadide kasutamisel tuleb arvestada, et erinevate laadidega identifikaatorid loetakse erinevateks muutujateks isegi siis kui tegemist on identsete sümbolitega. Väärib veel märkimist, et tekstipiirkonnad ja matemaatikapiirkonnad reageerivad erinevalt, kui tööriistaribalt Formatting muuta šrifti omadusi. Tekstipiirkonna korral rakendub muudatus vaid valitud tekstiosale, arvutuspiirkonna puhul aga muudetakse kohe aktiivset laadi. Seetõttu matemaatikalaadide eraldi redigeerimist harilikult tarvis ei lähegi.
Kuivõrd Mathcad pole tekstitoimeti tavapärases mõttes, siis sisestamisel ei toimu plokkide automaatset ümberpaigutamist vältimaks kattumisi.Tekstipiirkonna omaduste dialoogis (kohtmenüüst Properties) saab siiski märgistada suvandi Push regions down as you type. Enter-klahvi vajutamine lükkab kõiki piirkondi ühe rea võrra allapoole, Del või Backspace teeb vastupidist. Hiirega on võimalik märgistada üks või mitu plokki ja lohistada neid kogu töölehe ulatuses saavutamaks soovitud paigutust ja õiget arvutuste järjekorda.
Lihtsad arvutused
 SisukordMathcad'i
lihtsaim rakendus on kasutamine kalkulaatorina (kasvõi klõpsides
nuppe vastavalt matemaatikapaletilt). Kalkulatsiooni tulemuse võib
lasta kohe võrdusmärgi järel kuvada, kuid selle saab omistada
ka mingile muutujale, mida saab seejärel kasutada juba järgmises
avaldises jne.
SisukordMathcad'i
lihtsaim rakendus on kasutamine kalkulaatorina (kasvõi klõpsides
nuppe vastavalt matemaatikapaletilt). Kalkulatsiooni tulemuse võib
lasta kohe võrdusmärgi järel kuvada, kuid selle saab omistada
ka mingile muutujale, mida saab seejärel kasutada juba järgmises
avaldises jne.
Funktsiooni väljakutsumiseks tuleb, nagu matemaatilises kirjapildis tavaks, lisada funktsiooni nime järgi sulgudesse argument (või komaga eraldatud argumendid). Kuivõrd Mathcad püüab järgida naturaalset matemaatilist kirjapilti, siis eraldi funktsioone juurimise (\), astendamise (^) ja absoluutväärtuse (|) jaoks ei lähe tarvis [muudes keskkondades sqrt(x), pow(x,y), abs(x) vms].

Nagu näha, esineb Mathcad'is mitmesuguseid "võrdusmärke".
Võrdusmärkide (ja ka korrutusmärgi) väljanägemist
saab muuta töölehe seadetest (Tools →
Worksheet Options →
Display).Muutuja
defineerimiseks on omistamise sümbol
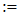 (klaviatuurilt koolon), muutuja või avaldise väärtuse
kuvamiseks aga tavaline võrdusmärk
(klaviatuurilt koolon), muutuja või avaldise väärtuse
kuvamiseks aga tavaline võrdusmärk
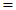 (sama sümbol ka kiirkorralduseks). Nagu pärastpoole selgub, on olemas
veel "rasvane" võrdusmärk
(sama sümbol ka kiirkorralduseks). Nagu pärastpoole selgub, on olemas
veel "rasvane" võrdusmärk
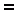 võrduse vasaku ja parema poole võrdsuse testimiseks, analüütilise
arvutamise operaator
võrduse vasaku ja parema poole võrdsuse testimiseks, analüütilise
arvutamise operaator
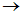 ning lokaalse omistamise operaator
ning lokaalse omistamise operaator
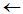 .
.
Avaldiste kirjapanemisel saab kasutada mitmeid kasulikke konstante (pigemini on tegemist küll muutujatega, sest neid on lubatud üle defineerida): naturaallogaritmide alus e=2.718, arv π=3.142, ühe nurgakraadi väärtus radiaanides deg=0.0175 ja protsent %=0.01. Kahte viimast on mugav kasutada dimensioonitu mõõtühiku rollis. Näiteks trigonomeetrilised funktsioonid ootavad nurka radiaanides, seega kraadides antav nurk tuleb korrutada konstandiga deg.

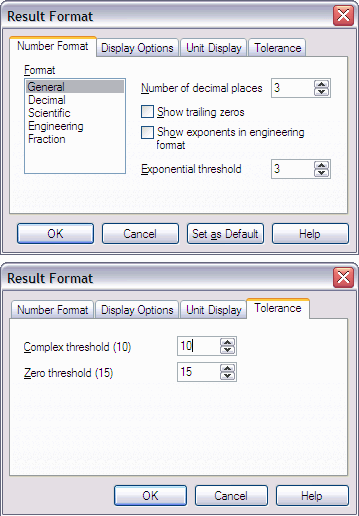 Vaikeseadetes
ei näidata arvutustulemust mitte maksimaalse võimaliku täpsusega,
vaid kuni 3 kohta peale koma, kusjuures tulemused mis on absoluutväärtuselt
väiksemad kui 10–15, ümardatakse nulliks. Viimane
on teadusarvutuste seisukohalt reeglina ebasobiv, sest näiteks mingi
füüsikalise suuruse väärtus (väljendatuna põhiühikutes)
võib olla ka hulga väiksem kui 10–15. Arvutusresultaadi
vormingu muutmiseks tuleb teha topelt-klõps tulemuse peal ja määrata
soovitud seaded avanevas dialoogikastis Result Format.
Märgime, et ekraanil näidatav täpsus ei mõjuta tegelikku,
mälus säilitatavat täpsust (kuigi arvu kopeerimine lõikepuhvri
vahendusel säilitab vaid kuvatava täpsuse). Mathcad'i numbrilised
arvutused toetuvad 32-bitiste protsessorite
topelt-täpsusega ujukomaarvudele, mille võimalikud absoluutväärtused
jäävad ligikaudu vahemikku 10–308…10308
ja täpsus on kuni 17 tüvenumbrit. Mathcad lubab kasutada reaalarve
absoluutväärtuste vahemikus 10–307…10307
(suurimat arvväärtust 10307 markeerib lõpmatusesümbol
∞). Sümbolarvutus, mis kasutab keerukamaid
andmestruktuure ja algoritme suurte arvudega opereerimiseks, pakub peaaegu
piiramatut arvutustäpsust, kuid mõistagi kiiruse arvelt (vt
allpool).
Vaikeseadetes
ei näidata arvutustulemust mitte maksimaalse võimaliku täpsusega,
vaid kuni 3 kohta peale koma, kusjuures tulemused mis on absoluutväärtuselt
väiksemad kui 10–15, ümardatakse nulliks. Viimane
on teadusarvutuste seisukohalt reeglina ebasobiv, sest näiteks mingi
füüsikalise suuruse väärtus (väljendatuna põhiühikutes)
võib olla ka hulga väiksem kui 10–15. Arvutusresultaadi
vormingu muutmiseks tuleb teha topelt-klõps tulemuse peal ja määrata
soovitud seaded avanevas dialoogikastis Result Format.
Märgime, et ekraanil näidatav täpsus ei mõjuta tegelikku,
mälus säilitatavat täpsust (kuigi arvu kopeerimine lõikepuhvri
vahendusel säilitab vaid kuvatava täpsuse). Mathcad'i numbrilised
arvutused toetuvad 32-bitiste protsessorite
topelt-täpsusega ujukomaarvudele, mille võimalikud absoluutväärtused
jäävad ligikaudu vahemikku 10–308…10308
ja täpsus on kuni 17 tüvenumbrit. Mathcad lubab kasutada reaalarve
absoluutväärtuste vahemikus 10–307…10307
(suurimat arvväärtust 10307 markeerib lõpmatusesümbol
∞). Sümbolarvutus, mis kasutab keerukamaid
andmestruktuure ja algoritme suurte arvudega opereerimiseks, pakub peaaegu
piiramatut arvutustäpsust, kuid mõistagi kiiruse arvelt (vt
allpool).
Ujukomaarvude lõpliku riistvaralise täpsuse tõttu võivad arvutustesse tekkida veidrad vead. Näiteks kui arvutustulemus peaks teoreetiliselt tulema täpselt võrdne nulliga, siis ümardusvea tõttu võib see tulla ikkagi nullist veidi erinev:
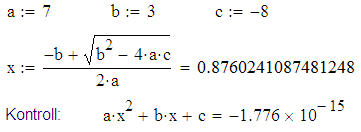
Mõõtühikud
Mathcad käsitleb kõiki arvväärtuseid kui potentsiaalseid füüsikalisi mõõte, st iga väärtus võib olla seotud mingi füüsikalise suuruse dimensiooniga. Seetõttu andmete sisestamisel saab ära näidata ka mõõtühikud ning järgnevates arvutustes suudab Mathcad juba automaatselt arvet pidada selle üle, kuidas erinevad dimensioonid kombineeruvad. SisukordMõõtühikute kasutamine Mathcad'is on väga loomulik: mõõtühiku rollis võib põhimõtteliselt kasutada mistahes muutujat (sh dimensioonituid muutujaid nagu deg või %), millega mõõtarv tuleb lihtsalt läbi korrutada. Lisaks tekib iga arvutustulemuse taha lünk, kuhu saab kirjutada selle mõõtühiku (muutuja) tähise, mille kaudu tulemust tahetakse esitada. Suur hulk muutujanimesid (näiteks kg, m, cm, K, A jne) on juba töölehe alguses vaikimisi seostatud vastavate ühikmõõtudega (kuid see ei takista neid vajadusel üle defineerimast ja muuks otstarbeks kasutamast). Täieliku ülevaate eeldefineeritud mõõtühikutest annab dialoog Insert → Unit. Spetsiifilisemaid ühikuid mõistagi Mathcad ei pruugi teada, need tuleb siis arvutuste alguses ise defineerida.Fundamentaalkonstantide väärtusi jm kasulikke andmeid saab kopeerida ressursikeskusest (Help → Reference Tables ).

Ühikute kasutamine arvutustes omab rida kasulikke efekte. Esiteks, lähteandmed ja arvutustulemused saab esitada kohe loomulikes (antud ainevallale traditsioonilistes) ühikutes, mis muudab teksti loetavamaks ja säästab ühikute teisendamise vajadusest. Teiseks, kui arvutusvalemid on valitud mõõtühikute süsteemis üldkujul ja korrektselt kirja pandud, siis arvutustulemus omandab automaatselt õige dimensiooni. Ühtlasi aitab see vältida vigu valemite sisestamisel, sest mitteühilduvate ühikute korral annab programm vastava veateate. Näiteks erinevate dimensioonidega suurusi ei saa kokku liita, dimensiooni omavast suurusest ei saa logaritmi võtta jne.

Ühikute kasutamisel on ka mõningaid piiranguid. Näiteks massiivi elemendid ei saa olla erinevate ühikutega, millest omakorda tuleneb, et võrrandite ja võrrandisüsteemide lahendamisel on ühikute kasutamine võimatu. Samuti on mõnikord arvutuste stabiilsuse huvides tarvilik, et sisendandmed oleks normeeritud mõistlikku diapasooni.
Andmetüübid
SisukordMathcad'is, nii nagu enamikes programmeerimiskeeltes, eksisteerib vähemalt kolme erinevat tüüpi andmeid: arvud, sõned ja massiivid. Iga andmetüübiga kaasneb hulk tüüpilisi operatsioone, mida vastavate andmetega saab teostada. Kõigis seni vaadeldud näidetes on opereeritud üksikute arvväärtuste ehk skaalaritega. String ehk eestipäraselt sõne sisaldab meelevaldset teksti (nt failinime). Stringi väärtused kuvatakse jutumärkide vahel. Näited:
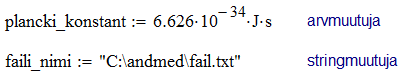
Nagu enamikele matemaatilise orientatsiooniga süsteemidele, on ka Mathcad'i sisse ehitatud toetus kompleksarvudele. See tähendab, et skalaarne väärtus võib üldjuhul olla kompleksarv ja enamus funktsioone on "teadlikud" kompleksarvulistest argumentidest. Näiteks ruutjuure või logaritmi arvutamine negatiivsest arvust on täiesti lubatav tegevus (iseasi, kas ka mõttekas). Seega mingeid ponnistusi kompleksarvuliste tulemuste või avaldiste vältimiseks ei ole tarvis teha. Imaginaararvulise väärtuse sisestamiseks tuleb vahetult arvu järele kirjutada kas i või j.
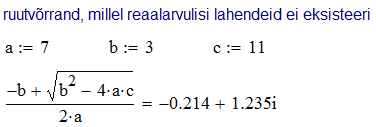
Kompleksarvude kasutamine võimaldab ökonoomselt kirja panna kompleksmeetodiga lahenduvate füüsikaliste või insenertehniliste probleemide vastuseid:

Siinkohal paneme tähele, et absoluutväärtuse võtmise |x| tähendus sõltub sellest, millist tüüpi matemaatilisele objektile x seda rakendatakse. Reaalarvude korral on selle tähendus absoluutväärtus, kompleksarvude korral moodul, vektorite korral norm (e. pikkus) ja maatriksite korral determinant.
 Massiiv
(array) on mingite andmeelementide indekseeritud järjend või
tabel. Elementideks võivad olla skaalarid, stringid või ka
teised massiivid. Valdavalt kasutatakse selliseid massiive, kus kõik elemendid
on sama tüüpi (enamasti skaalarid). Massiivi iga elemendi poole saab individuaalselt
pöörduda tema järjekorranumbri abil, mis kuvatakse alaindeksina. Ühemõõtmelist
(ühe indeksiga adresseeritavat) massiivi nimetatakse
vektoriks, kahemõõtmelist massiivi
maatriksiks. Massiivi esimese elemendi indeksi
määrab Mathcad'i sisemine muutuja ORIGIN,
mille vaikeväärtus on null. Mõningail juhtudel võib
mugavam olla siiski loendamise alustamine 1-st. Selliste süsteemimuutujate
väärtusi saab defineerida kas otse töölehel või
siis töölehe seadete dialoogist (Tools →
Worksheet Options →
Built-in Variables).
Massiiv
(array) on mingite andmeelementide indekseeritud järjend või
tabel. Elementideks võivad olla skaalarid, stringid või ka
teised massiivid. Valdavalt kasutatakse selliseid massiive, kus kõik elemendid
on sama tüüpi (enamasti skaalarid). Massiivi iga elemendi poole saab individuaalselt
pöörduda tema järjekorranumbri abil, mis kuvatakse alaindeksina. Ühemõõtmelist
(ühe indeksiga adresseeritavat) massiivi nimetatakse
vektoriks, kahemõõtmelist massiivi
maatriksiks. Massiivi esimese elemendi indeksi
määrab Mathcad'i sisemine muutuja ORIGIN,
mille vaikeväärtus on null. Mõningail juhtudel võib
mugavam olla siiski loendamise alustamine 1-st. Selliste süsteemimuutujate
väärtusi saab defineerida kas otse töölehel või
siis töölehe seadete dialoogist (Tools →
Worksheet Options →
Built-in Variables).
Massiivide tekitamiseks on mitmeid võimalusi. Suhteliselt vähe elemente sisaldava massiivi võib sisse toksida käsitsi. Kasutada saab nii traditsioonilist maatriksi kuva (Insert → Matrix ehk Ctrl+M) kui ka veidi mugavamat tabelit (Insert → Data → Table):.
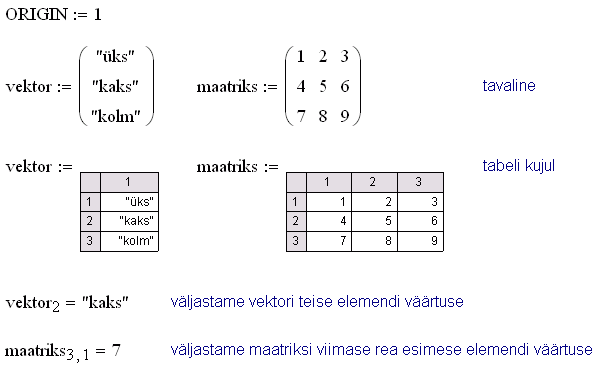
Siinkohal tasub tähele panna, et Mathcad'is esineb kahte tüüpi alaindekseid: massiivi indeks, millega pöördutakse massiivi konkreetse elemendi poole (kiirkorraldus [), ja nn "iluindeks", mis on lihtsalt osa muutujanimest ega kanna iseseisvat tähendust (kiirkorraldus .). Seega massiivi indeks on üldjuhul täisarvulise väärtusega matemaatiline avaldis, "iluindeks" võib olla aga meelevaldne sümbolite jada.
Üks praktiline vajadus massiivide järgi tekib siis, kui on tarvis läbi töötada suur hulk ühetaoliseid andmeid. Sellised andmemassiivid tekivad näiteks mitmesuguste füüsikaliste mõõtmiste käigus (voolutugevuse sõltuvus pingest, optilise signaali sõltuvus lainepikkusest, deformatsiooni sõltuvus rakendatud jõust, jne). Iga selline andmemassiiv võib sisaldada tuhandeid katsepunkte. Veelgi enam, eksperimendi tulemuseks võib olla suur hulk sarnase iseloomuga andmemassiive, mille analüüs või teisendamine oleks mõistlik automatiseerida. Selliseid mahukaid andmeid on mõistlik Mathcad'i massiivi sisse lugeda failist. Mõõteaparatuuri juhtprogramm lubab sageli mõõtmistulemuse salvestada struktureeritud tekstiformaadis, kus arvutulbad on eraldatud tühikute, tabulatsioonisümboli või komaga. Kõige lihtsamini saab sellise faili sisu Mathcad'i maatriksmuutujasse kasutades funktsiooni READPRN (või READCSV, kui on komaga eraldatud väärtused). Nimetatud funktsiooni argumendiks on faili nimi (string). Tavaliselt andmefail asetatakse samasse kataloogi, kus paikneb Mathcad'i töölehe fail; sel juhul kataloogi ei pea funktsioonile READPRN antavas failinimes ära näitama.Täpsemalt, funktsioonid READPRN, WRITEPRN ja kõik teised failist lugemise või faili kirjutamise funktsioonid otsivad faili kataloogist, mille määrab süsteemimuutuja CWD (Current Working Directory). Vaikimisi osutab CWD sellele kataloogile, kus asub töölehe fail. Nii nagu muutujat ORIGIN, võib ka CWD vastavalt vajadusele üle defineerida. Näiteks, kui andmefailid on paigutatud kõik alamkataloogi nimega "andmed", siis tuleks töölehe alguses anda käsk CWD := concat(CWD, "andmed"). Peale andmete töötlemist võib vaja minna ka analoogilist funktsiooni WRITEPRN töödeldud massiivi väljastamiseks faili (et seda oleks võimalik mingis teises programmis vormistada või edasi töödelda). WRITEPRN-iga kirjutatava faili formaati saab kontrollida süsteemimuutujatega PRNPRECISION ja PRNCOLWIDTH. Esimene määrab faili kirjutatava arvu täpsuse (vaikimisi 4 tüvenumbrit), teine aga igale arvutulbale reserveeritava veeru laiuse (vaikimisi 8 sümbolit).

Märgime, et kui maatriks defineerida tabeli abil, siis tabelisse saab (mahukad) andmed ka kleepida, seda muidugi tingimusel et andmed on Windowsi lõikelaual olemas sobivas formaadis (näiteks struktureeritud tekstina).
Viimaks, massiivi saab luua (ja selle elemente modifitseerida) ka arvutuslikult. Selleks on tarvilik indeksmuutujate defineerimine (kiirkorraldus ;), mis lubab järgemööda läbi käia kõik massiivi elemendid. Indeksmuutuja on erivariant üldisemast vahemikmuutujast erinedes viimasest vaid selle poolest, et väärtused on täisarvulised ja samm on 1 (seetõttu viimast ei pea ära näitama).
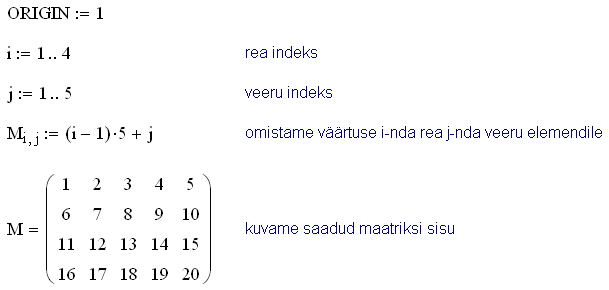
Niisiis indeksi(te) abil saab lugeda/kirjutada massiivi üksikuid elemente. Lisaks on olemas ka veeruoperaator (Ctrl+6), mille kaudu saab pöörduda maatriksi veeruvektori poole. Viimane on samuti nii loetav kui ka ülekirjutatavMärgime, et otseselt reavektori poole pöördumise võimalust ei ole, ilmselt sellepärast, et mälus säilitatakse maatriksit veeruvektorite kaupa. . Viimaks, funktsiooni submatrix abil saab väljastada etteantud piirides alam-maatriksi.

Tundmatu või varieeruva suurusega massiivide töötlemisel tuleks kasutada vastavaid funktsioone massiivi suuruse määramiseks (võimalusel tuleks tööleht kavandada nii, et see toimiks mistahes mahuga sisendandmete korral):
| length(V) | elementide arv vektoris |
|---|---|
| last(V) | vektori viimase elemendi indeks |
| rows(M) | ridade arv maatriksis |
| cols(M) | veergude arv maatriksis |
Veel mõningaid kasulikke funktsioone massiivide kombineerimiseks ja elementide ümberjärjestamiseks:
| augment(A,B) | seab kaks massiivi üksteise kõrvale (kui nende ridade arv klapib) |
|---|---|
| stack(A,B) | seab kaks massiivi üksteise kohale (kui nende veergude arv klapib) |
| reverse(M) | muudab massiivi ridade järjekorra vastupidiseks |
| csort(M,n) | sorteerib maatriksi read etteantud indeksiga veeru järgi kasvavasse järjekorda |
Mathcad püüab kõiki operatsioone massiivide vahel tõlgendada lineaaralgebra mõttes. Näiteks kahe võrdse pikkusega vektori korrutis ei anna tulemuseks mitte nende vastavate elementide korrutiste vektorit, vaid vektorite skalaarkorrutise, mis on järgmisel viisil defineeritud skalaarne väärtus: \[\vec a\cdot\vec b=a_1b_1+a_2b_2+\ldots+a_nb_n.\] Sellised spetsiifilised vektor- ja maatriksoperatsioonid kajastavad tegelikult teatavaid sageliesinevaid arvutusmustreid reaalsetes matemaatilistes probleemides. mis hõlmavad suuri andmekogumeid. Teisisõnu, nende abil on sageli võimalik suurt hulka elementaarseid arvutustehteid sisaldav algoritm väga kompaktselt kirja panna (vt näiteks viide või regressioonsirge sobitamise ülesanne allpool). Selleks et massiividega meelevaldseid arvutusoperatsioone läbi viia (mis ei ole esitavad lineaaralgebralise tehte kujul), tuleb need arvutused kas otse elementide kaupa välja kirjutada (kasutades indeksmuutujaid) või siis (erijuhtudel) rakendades avaldisele nn vektoriseerimisoperaatorit (vectorize, kiirkorraldus Ctrl++):

Graafikud
Sisukord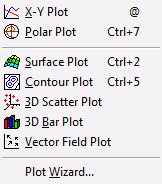 Graafiku
loomiseks tuleb esmalt tekitada graafiku toorik, valides sobiva graafikutüübi
alam-menüüst Insert →
Graph (või graafikute paletilt). Kõige
lihtsam ja kõige sagedamini vaja minev on ristkoordinaadistikuga
2D graafik (X-Y Plot, kiirkorraldus @).
Tooriku kummalgi teljel (all ja vasakul) on kolm tühja kastikest ehk
lünka. Keskmistesse kastikestesse tuleb kirjutada andmed või avaldised,
mida soovitakse graafikul kuvada, äärmistesse kastikestesse võib
aga vajadusel kirjutada skaala algus- ja lõppväärtused
(ka need võib esitada mingi avaldisena, et arvutuslikult kontrollida graafiku
diapasooni). Graafikul kuvatavad kõverad antakse harilikult ette kas (1)
vektoritena (võrdse pikkusega) või (2) üht ja sama vahemikmuutujat sisaldavate
avaldistena. Viimase erijuhuks on näiteks indeksmuutuja ühel teljel ning
vastav massiivi element teisel teljel. Rohkem kui ühe kõvera
kuvamiseks tuleb avaldised eraldada komaga. Seejuures ühele teljele (näiteks
alumisele) võib jätta ainult ühe avaldise juhul kui kõigi kõverate diapasoonid
on ühesugused, nagu järgmises näites.
Graafiku
loomiseks tuleb esmalt tekitada graafiku toorik, valides sobiva graafikutüübi
alam-menüüst Insert →
Graph (või graafikute paletilt). Kõige
lihtsam ja kõige sagedamini vaja minev on ristkoordinaadistikuga
2D graafik (X-Y Plot, kiirkorraldus @).
Tooriku kummalgi teljel (all ja vasakul) on kolm tühja kastikest ehk
lünka. Keskmistesse kastikestesse tuleb kirjutada andmed või avaldised,
mida soovitakse graafikul kuvada, äärmistesse kastikestesse võib
aga vajadusel kirjutada skaala algus- ja lõppväärtused
(ka need võib esitada mingi avaldisena, et arvutuslikult kontrollida graafiku
diapasooni). Graafikul kuvatavad kõverad antakse harilikult ette kas (1)
vektoritena (võrdse pikkusega) või (2) üht ja sama vahemikmuutujat sisaldavate
avaldistena. Viimase erijuhuks on näiteks indeksmuutuja ühel teljel ning
vastav massiivi element teisel teljel. Rohkem kui ühe kõvera
kuvamiseks tuleb avaldised eraldada komaga. Seejuures ühele teljele (näiteks
alumisele) võib jätta ainult ühe avaldise juhul kui kõigi kõverate diapasoonid
on ühesugused, nagu järgmises näites.
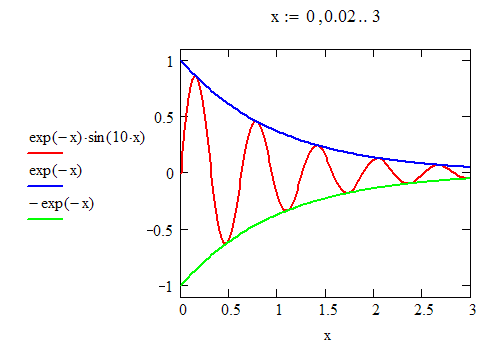
Graafik polaarkoordinaatides (Insert → Graph → Polar Plot) toimib täiesti analoogiliselt, vaid x- ja y-väärtuste asemel tuleb anda nurk (x-telje suhtes) ja kaugus koordinaatide alguspunktist.
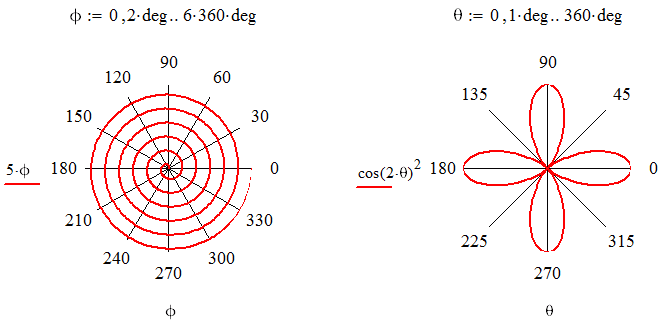
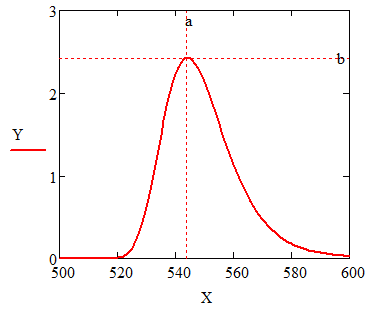
Peale graafikul kuvatavate andmete ning skaala piiride muud aspektid graafiku väljanägemises ei ole koodiga kontrollitavad, vaid need tuleb määrata graafiku peal topeltklõpsu tehes avanevast dialoogist (või valides kohtmenüüst Format). Kuivõrd graafikute peamine otstarve Mathcad'is on eelkõige visualiseerida jooksvalt arvutustulemusi, siis eriti põhjalikke vormindusvahendeid ei eksisteeri. Lehel X-Y Axes saab eraldi kummagi koordinaattelje jaoks määrata kas skaala on lineaarne või logaritmiline (Log scale), kas ja millise värviga näidata skaala abijooni (Grid lines) jms. Lehel Traces saab kõigile andmeseeriatele anda nime ning määrata nende väljanägemise (andmepunktide ning neid ühendavate sirgjoonte tüübi, suuruse ja värvi). Kui peita ära telgedel olevad avaldised (Hide arguments), teha sobivas kohas nähtavaks legend (Hide legend) ning lehel Labels sisestada telgede ja graafiku nimetused, saame juba üsna talutavalt vormistatud graafiku:
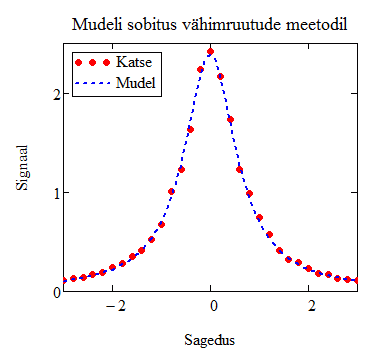
Graafiku kohtmenüüst on käivitatavad kasulikud vahendid Trace (hiirekursori kohal oleva punkti koordinaatide näitamine) ja Zoom (valitud ala suurendamine). Graafiku vormindamise dialoogis saab samuti aktiveerida kummagi telje jaoks suvandi Show markers, mis lubab graafikul märgistada kummalgi teljel kuni kaks positsiooni.
Funktsioonid
SisukordKuigi Mathcad pakub üsna avara valiku funktsioone mitmesuguste ülesannete täitmiseks (vt Insert → Function), muutub vähegi keerulisema arvutuse või andmetöötluse organiseerimisel vajalikuks ka uute funktsioonide defineerimine ning programmeerimisvahendite kasutamine (märksõnad IF, FOR, WHILE jne). Programmeerimistemaatikaga tegeleme järgmises punktis.
Funktsiooniks nimetame üldiselt mingit kindlat eeskirja või algoritmi, mis igale etteantud elemendile teatud hulgast seab vastavusse mõne teise elemendi, mis kuulub samasse või mõnda erinevasse hulka. Vastavalt räägitakse funktsiooni argumendist (ehk parameetrist) ja funktsiooni väärtusest. Uue funktsiooni defineerimisel tuleb seega ära näidata nii argumendi tähis kui ka sellest argumendist sõltuv avaldis, mille põhjal arvutatakse funktsiooni väärtus. Ainus väline erinevus muutuja ja funktsiooni definitsioonide vahel on argumendi tähise lisamine funktsiooni nime järgi sulgudes. Mathcad'is võivad funktsiooni argumendid ja tagastusväärtused olla täisarvud, reaalarvud, kompleksarvud, arvumaatriksid, stringid või ka mingid muud massiivide baasil realiseeritud agregaadid.
Üks lihtsamaid funktsioone on näiteks ruutfunktsioon, mis võtab argumendi, korrutab selle iseendaga (st tõstab astmesse 2) ning tagastab saadud korrutise väärtuse. See funktsioon suudab opereerida nii reaalarvudega, kompleksarvudega kui ka ruutmaatriksitega:

Sellel funktsioonil paraku suurt praktilist väärtust ei ole, sest Mathcad'i süntaktilised võimalused lubavad vajadusel iga avaldise ka niisama ruutu tõsta. Mingi praktiline väärtus võiks juba olla funktsioonil, mis tagastab ruutvõrrandi lahendi. See funktsioon vajab juba kolme parameetrit. Veelgi enam, me saame kahe-elemendilise vektorina tagastada korraga ruutvõrrandi mõlemad lahendid. Nii funktsiooni defineerimisel kui ka väljakutsumisel argumendid eraldatakse komaga.
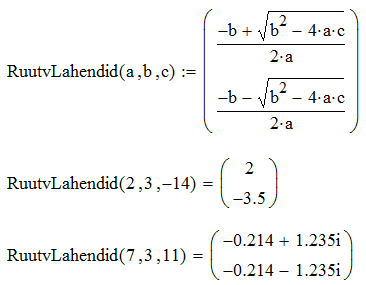
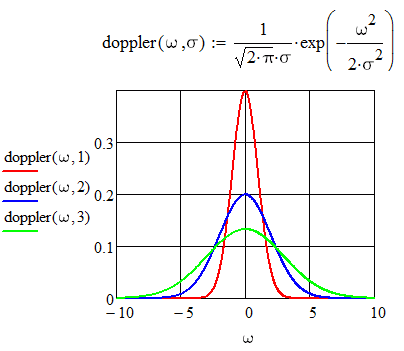
Märgime, et funktsiooni sisulist tähendust arvestades võivad selle argumendid olla üsna erineva iseloomuga funktsiooni väärtuse määramisel. Näiteks järgnevas näites funktsioon doppler(ω,σ) on sisuliselt ω-st sõltuv ühe muutuja funktsioon, kuid selle sõltuvuse kuju on omakorda kontrollitav parameetriga σ. Trükitud tekstis oleks võimalik seda spetsiaalselt rõhutada näiteks sellise kirjapildiga: \(\mathop{\rm doppler}_\sigma(\omega)\), kuid arvuti jaoks tuleb mõlemad parameetrid esitada ühesugusel viisil:
 Mõningatel
juhtudel on hädavajalik defineerida funktsioon mitmes osas, sõltuvalt parameetri
väärtusest. Vaatleme näiteks funktsiooni \(\mathop{\rm sinc}(x)=\sin(x)/x\).
Siin on potentsiaalne probleem selles, et kui \(x=0\), siis tekib määramatus
\(0/0\), kuigi piirväärtus on võrdne 1-ga. Üldjuhul saab kuitahes keerulisi
valikuid teostada programmeerimisvahenditega, aga Mathcad pakub lihtsamateks
vajadusteks funktsiooni if(tingimus, kui_tõene, kui_väär).
Kui esimese argumendina antud tingimus on tõene, siis tagastatakse teise
argumendi väärtus, vastasel korral kolmanda argumendi väärtus. Tingimuse
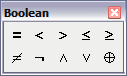
kirjeldamisel saab kasutada operaatoreid paletilt
Boolean (suurem, väiksem, võrdne jne). Mathcad'is loetakse tõeseks
iga avaldis, mille väärtus erineb nullist.Paljudes programmeerimiskeeltes
on olemas eraldi "bool" või "boolean" andmetüüp loogikaavaldiste
tarbeks; Mathcad'is seda ei ole. Keerukama tingimuse saamiseks võib
elementaarseid võrdlusoperatsioone ka kombineerida (sellel peatume edaspidi).
Seega funktsioon \(\mathop{\rm sinc}\) tuleks defineerida järgmiselt:
Mõningatel
juhtudel on hädavajalik defineerida funktsioon mitmes osas, sõltuvalt parameetri
väärtusest. Vaatleme näiteks funktsiooni \(\mathop{\rm sinc}(x)=\sin(x)/x\).
Siin on potentsiaalne probleem selles, et kui \(x=0\), siis tekib määramatus
\(0/0\), kuigi piirväärtus on võrdne 1-ga. Üldjuhul saab kuitahes keerulisi
valikuid teostada programmeerimisvahenditega, aga Mathcad pakub lihtsamateks
vajadusteks funktsiooni if(tingimus, kui_tõene, kui_väär).
Kui esimese argumendina antud tingimus on tõene, siis tagastatakse teise
argumendi väärtus, vastasel korral kolmanda argumendi väärtus. Tingimuse
kirjeldamisel saab kasutada operaatoreid paletilt
Boolean (suurem, väiksem, võrdne jne). Mathcad'is loetakse tõeseks
iga avaldis, mille väärtus erineb nullist.Paljudes programmeerimiskeeltes
on olemas eraldi "bool" või "boolean" andmetüüp loogikaavaldiste
tarbeks; Mathcad'is seda ei ole. Keerukama tingimuse saamiseks võib
elementaarseid võrdlusoperatsioone ka kombineerida (sellel peatume edaspidi).
Seega funktsioon \(\mathop{\rm sinc}\) tuleks defineerida järgmiselt:
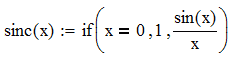
Paljud programmeerimiskeeled (sh Mathcad) lubavad ühe huvitava võimaluse funktsioonide defineerimisel: nimelt funktsiooni kehaks olev programmikood tohib ka sedasama funktsiooni (st iseennast) välja kutsuda (tõenäoliselt mõnevõrra erinevate parameetritega). Seda nimetatakse rekursiooniks. Üldiselt saab iga probleemi lahendada ilma rekursioonita, kuid rekursioon võimaldab sageli lahenduse formuleerida märksa kiiremini ja elegantsemalt. Vaatleme seekord näitena finantsülesannet. Alghetkel on pangakontol €1000. Iga kuu lõpus lisanduvad säästud €50. Hoiustamisest saadav igakuine intress on 0,5% kuu alguses eksisteerivast rahasummast. Milline on konto seis 10 a. pärast? Olgu \(K(n)\) kontol olev rahasumma peale \(n\) kuu möödumist. Ilmselt \(K(n)=(1+r)K(n-1)+S\), kus \(r\) on intress ja \(S\) on igakuine sissemakse. Saadud rekursiivne avaldis \(K(n)\) jaoks ongi sisuliselt ülesande lahendus. Niisiis, kui see algoritm on esitatud Mathcad'i funktsioonina K(n), siis viimane peab tulemuse saamiseks pöörduma uuesti iseenda poole argumendiga n–1. Samas on ilmne, et selline rekursiivne protsess ei saa jätkuda piiramatult. Lõpetamise tingimuseks on antud juhul \(n=0\), mille jaoks vastus on juba teada: \(K(0)=K_0\).
Et \(K(n)\) jaoks ilmutatud kujul analüütilist avaldist leida, tuleks vaadata selle sõltuvuse mõningaid lihtsamaid avaldisi nagu \(K(1)\), \(K(2)\) ja \(K(3)\), tabada ära \(K\) ja \(n\) vaheline seos ning vajadusel seda kontrollida kasutades matemaatilist induktsiooni. Saadav tulemus on allpool võrdluseks ära toodud.

Selgub et funktsioone võib vaadelda veel ühe omaette andmetüübina (lisaks skaalaritele, stringidele ja massiividele). Funktsiooni nimi ehk tähis ehk identifikaator on lihtsalt muutuja, mis viitab sellele kohale arvuti mälus, kus funktsiooni defineeriv kood tegelikult asub. Miski ei keela mitmel erineval funktsiooninimel viitamast ühele ja samale kohale mälus. Teisisõnu, funktsiooni viidet võib kopeerida ja seda võib edastada mõne teise funktsiooni argumendina või tagastusväärtusena. Selle idee rakendusnäitena vaatleme erinevate ühe muutuja funktsioonide graafikute sirvimise programmi, kus ainus liigutus, mida kasutaja peab tegema, on funktsiooni nime sisestamine. Seega programm peab vastavalt valitud funktsioonile valima ka kõige sobivama x-telje diapasooni graafiku kuvamiseks. Selleks võtame kasutusele kaks ühesuguse pikkusega vektorit, kus vektor FUN säilitab funktsioonide viiteid ja vektor DIAP säilitab x-telje minimaalse ja maksimaalse väärtuse (kahe-elemendilise vektorina). Kasutaja poolt sisestatud funktsiooni nimi on aga täisarvuline indeks, millega valitakse kummastki nimetatud vektorist vastav element.
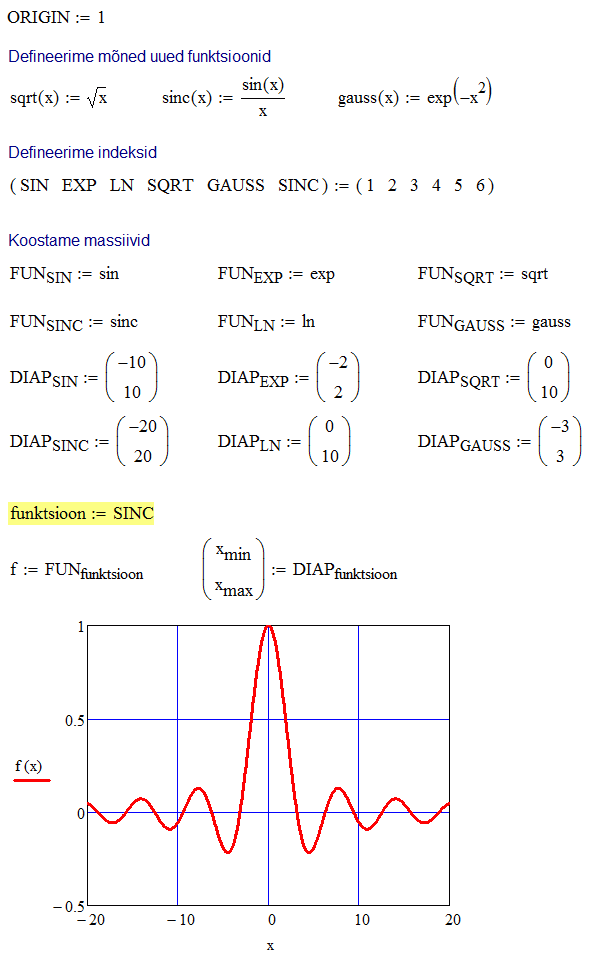
Toodud näite ainus puudus seisneb selles, et funktsioonide graafikuid uurides võivad kasutajat häirida ülejäänud tehnilised aspektid (massiivide väärtustamised jne). Sellised ebahuvitavad detailid saab ära peita kollapseeruvate piirkondade sisse, milliseid saab luua käsuga Insert → Area. Piirkonna avanemine/sulgumine toimub hiire topelt-klõpsuga. Kontekstimenüüst käsuga Properties avanevas dialoogis saab piirkonnale anda ka nime.
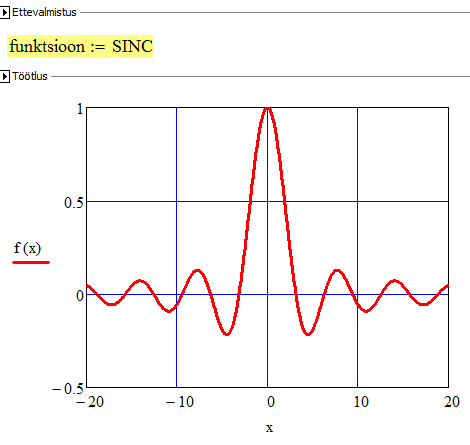
 Tavalised
aritmeetilised operatsioonid (liitmine, lahutamine jne) on tegelikult samuti
binaarsed (st kahe argumendiga) funktsioonid, mille üleskirjutamisel kasutatakse
lihtsalt teistsugust tähistust: funktsiooni nimi ehk operaator kirjutatakse
kahe argumendi (ehk operandi) vahele. Sellisel kujul väljakutsutavat funktsiooni
nimetatakse infiks-operaatoriks. Leitub ka mitmeid operaatorina rakendatavaid
unaarseid funktsioone nagu arvu märgi pööramine ja loogiline eitus. Mathcad
lubab ka kasutaja defineeritud funktsioone sellisel kujul rakendada. Selleks
tuleb paletilt Evaluation valida vastavalt
vajadusele kas Infix Operator,
Prefix Operator või Postfix
Operator. Selline tegevus omab mingit mõtet muidugi vaid juhul kui
see teeb matemaatilist kirjapilti selgemaks. Operaatorina rakendatava funktsiooni
tähiseks tuleks võtta mingisugune erisümbol, milliseid saab valida näiteks
töölehelt Help →
QuickSheets → Extra Math Symbols.
Järgnevas näites kasutatakse operaatorina funktsiooni, millega on mugav
arvutada takistite rööpühenduse takistust.
Tavalised
aritmeetilised operatsioonid (liitmine, lahutamine jne) on tegelikult samuti
binaarsed (st kahe argumendiga) funktsioonid, mille üleskirjutamisel kasutatakse
lihtsalt teistsugust tähistust: funktsiooni nimi ehk operaator kirjutatakse
kahe argumendi (ehk operandi) vahele. Sellisel kujul väljakutsutavat funktsiooni
nimetatakse infiks-operaatoriks. Leitub ka mitmeid operaatorina rakendatavaid
unaarseid funktsioone nagu arvu märgi pööramine ja loogiline eitus. Mathcad
lubab ka kasutaja defineeritud funktsioone sellisel kujul rakendada. Selleks
tuleb paletilt Evaluation valida vastavalt
vajadusele kas Infix Operator,
Prefix Operator või Postfix
Operator. Selline tegevus omab mingit mõtet muidugi vaid juhul kui
see teeb matemaatilist kirjapilti selgemaks. Operaatorina rakendatava funktsiooni
tähiseks tuleks võtta mingisugune erisümbol, milliseid saab valida näiteks
töölehelt Help →
QuickSheets → Extra Math Symbols.
Järgnevas näites kasutatakse operaatorina funktsiooni, millega on mugav
arvutada takistite rööpühenduse takistust.
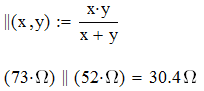
Programmeerimine
 SisukordKuigi Mathcad'i töölehte ennast
võib tervikuna vaadelda kui teatud laadi arvutiprogrammi, nimetatakse Mathcad'i
terminoloogias programmiks vaid selliseid konstruktsioone,
kus on kasutatud paletilt Programming pärinevaid
vahendeid. Selguse huvides nimetame selliseid konstruktsioone edaspidi siiski
alamprogrammideks. Kui enamikes programmeerimiskeeltes ja -vahendites kirjutatakse
programmikood vabas paigutuses lihttekstina, siis Mathcad'is on programmi
struktuur rangelt ette antud: iga paletil Programming
leiduva nupukese vajutus tekitab vastava programmielemendi tooriku, kus
kasutaja peab täitma vaid ettenäidatud tühikud. Seetõttu võtmesõnu
IF, FOR, WHILE jne käsitsi sisse toksida ei ole lubatud. Nupu
Add Line (]) vajutus
lisab alamprogrammile uusi ridu; tühja rea kustutamine toimub
Del või Backspace klahviga.
SisukordKuigi Mathcad'i töölehte ennast
võib tervikuna vaadelda kui teatud laadi arvutiprogrammi, nimetatakse Mathcad'i
terminoloogias programmiks vaid selliseid konstruktsioone,
kus on kasutatud paletilt Programming pärinevaid
vahendeid. Selguse huvides nimetame selliseid konstruktsioone edaspidi siiski
alamprogrammideks. Kui enamikes programmeerimiskeeltes ja -vahendites kirjutatakse
programmikood vabas paigutuses lihttekstina, siis Mathcad'is on programmi
struktuur rangelt ette antud: iga paletil Programming
leiduva nupukese vajutus tekitab vastava programmielemendi tooriku, kus
kasutaja peab täitma vaid ettenäidatud tühikud. Seetõttu võtmesõnu
IF, FOR, WHILE jne käsitsi sisse toksida ei ole lubatud. Nupu
Add Line (]) vajutus
lisab alamprogrammile uusi ridu; tühja rea kustutamine toimub
Del või Backspace klahviga.
Alamprogrammis on küll "nähtavad" eespool defineeritud
(globaalsed) muutujad, kuid viimaste väärtuse muutmine pole lubatud.
Seetõttu tarvitatakse alamprogrammides tavalise omistamise märgi
![]() asemel teistsugust omistusmärki
asemel teistsugust omistusmärki
![]() ,
millega saab defineerida lokaalseid muutujaid (kiirkorraldus
{). Lokaalsetele muutujatele omistatud väärtused
lähevad peale alamprogrammi töö lõppu kaotsi; ainus
info mis alamprogrammist välja pääseb, on RETURN-käsuga
tagastatud väärtus (või lihtsalt alamprogrammi viimase avaldise
väärtus). Alamprogrammi töö lõppedes lokaalsetele muutujatele
tellitud mälu vabastatakse, seega töölehe mälukasutuse
piiramise huvides on otstarbekas mitme-etapilised (vahetulemustega) arvutused
suurte andmemassiividega realiseerida alamprogrammina.
,
millega saab defineerida lokaalseid muutujaid (kiirkorraldus
{). Lokaalsetele muutujatele omistatud väärtused
lähevad peale alamprogrammi töö lõppu kaotsi; ainus
info mis alamprogrammist välja pääseb, on RETURN-käsuga
tagastatud väärtus (või lihtsalt alamprogrammi viimase avaldise
väärtus). Alamprogrammi töö lõppedes lokaalsetele muutujatele
tellitud mälu vabastatakse, seega töölehe mälukasutuse
piiramise huvides on otstarbekas mitme-etapilised (vahetulemustega) arvutused
suurte andmemassiividega realiseerida alamprogrammina.

Kuigi alamprogramme on võimalik kasutada ühekordselt mõne muutuja väärtuse arvutamiseks (nagu äsjases näites), saab neid mõistagi utiliseerida ka funktsioonide defineerimisel, mis lubab üht ja sama programmi erinevate parameetritega korduvalt välja kutsuda. Seejuures funktsiooni argumendid on alamprogrammi seisukohalt lokaalsed muutujad, nii et vajadusel võib nende väärtused alamprogrammi sees üle defineerida, ilma et see väliseid arvutusi mõjutaks. Järgnev näide realiseerib alamprogrammina palgakalkulaatori.

Senistes näidetes pole programmeerimisalaseid juhtstruktuure veel tarvis
läinudki. Nendel peatume järgnevas. Üks lihtsamaid programmielemente on
tingimuslause ehk IF-lause. See on lihtsaim (ja Mathcad'is ka ainus) juhtstruktuur,
mis võimaldab programmil hargneda. IF-lause toorik on järgmine:
![]() .
Paremasse kastikesse kirjutatakse tingimus ja vasakusse kastikesse tegevus,
mis täidetakse vaid selle tingimuse tõesuse korral. See tegevus võib kujutada
endast samuti pikemat programmi, mis sisaldab omakorda IF-lauseid jm programmielemente
jne. Vahetult IF-lausele võib järgneda võtmesõna OTHERWISE sisaldav struktuur
.
Paremasse kastikesse kirjutatakse tingimus ja vasakusse kastikesse tegevus,
mis täidetakse vaid selle tingimuse tõesuse korral. See tegevus võib kujutada
endast samuti pikemat programmi, mis sisaldab omakorda IF-lauseid jm programmielemente
jne. Vahetult IF-lausele võib järgneda võtmesõna OTHERWISE sisaldav struktuur
![]() .
Selle ainsasse kastikesse tuleb kirjutada käsud, mis kuuluvad täitmisele
juhul kui IF-lause tingimus osutus vääraks. Enamikes teistes programmeerimiskeskkondades
kasutatakse selle asemel võtmesõna ELSE. Järgnev näide esitab funktsiooni,
mis tagastab eksamihinde sõltuvana kogutud punktide arvust. Koostame selle
kahes variandis. Üks versioon kasutab OTHERWISE-lauset ülejäänud variantide
läbivaatamiseks. Teine versioon aga viib iga tõese tingimuse korral RETURN-käsuga
kohe alamprogrammist välja, nii et IF-lausele järgnevate käskudeni programmi
täitmisjärg ei jõuagi ja seega OTHERWISE-lauset ei lähe tarvis.
.
Selle ainsasse kastikesse tuleb kirjutada käsud, mis kuuluvad täitmisele
juhul kui IF-lause tingimus osutus vääraks. Enamikes teistes programmeerimiskeskkondades
kasutatakse selle asemel võtmesõna ELSE. Järgnev näide esitab funktsiooni,
mis tagastab eksamihinde sõltuvana kogutud punktide arvust. Koostame selle
kahes variandis. Üks versioon kasutab OTHERWISE-lauset ülejäänud variantide
läbivaatamiseks. Teine versioon aga viib iga tõese tingimuse korral RETURN-käsuga
kohe alamprogrammist välja, nii et IF-lausele järgnevate käskudeni programmi
täitmisjärg ei jõuagi ja seega OTHERWISE-lauset ei lähe tarvis.

IF-ELSE lause primitiivseim variant on valiku teostamine kahe väärtuse
vahel. Sellist konstruktsiooni saab realiseerida ka funktsiooni kujul (Mathcad'is
funktsioon if, mida sai kasutatud juba eespool).
Lisaks IF-lausele on programmeerimises hädavajalikud juhtstruktuurid mitmesugused
tsüklid. Mathcad'is on olemas määratud kordustega
ehk FOR-tsükkel ning eelkontrolliga ehk WHILE-tsükkel. FOR-tsükli idee seisneb
selles, et defineeritakse teatav tsüklimuutuja
ehk loendur, mis omandab järgemööda kõik väärtused
etteantud hulgast. FOR-tsükli toorik on järgmine:
 .
Esimesse kastikesse läheb loenduri tähis, teise kastikesse aga loenduri
väärtuse muutumise piirkond. Selle kirjeldamiseks pakub Mathcad neli varianti:
indeksväärtus (näiteks 1..10), vahemikväärtus
(näiteks 380,390..750), komaga eraldatud väärtused
või mingite väärtuste vektor. Lõpuks kolmandasse kastikesse läheb tsükli
keha, st käsud, mida tuleb loenduri iga väärtuse korral täita. WHILE-tsükli
toorik on veidi lihtsam:
.
Esimesse kastikesse läheb loenduri tähis, teise kastikesse aga loenduri
väärtuse muutumise piirkond. Selle kirjeldamiseks pakub Mathcad neli varianti:
indeksväärtus (näiteks 1..10), vahemikväärtus
(näiteks 380,390..750), komaga eraldatud väärtused
või mingite väärtuste vektor. Lõpuks kolmandasse kastikesse läheb tsükli
keha, st käsud, mida tuleb loenduri iga väärtuse korral täita. WHILE-tsükli
toorik on veidi lihtsam:
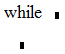 .
Esimesse kastikesse kirjutatakse tõeväärtust omav avaldis, teise kastikesse
aga käsud, mille täitmist jätkatakse seni kuni selle avaldise tõeväärtus
muutub vääraks. Klassikaline näide kummagi tsükli kohta on faktoriaali arvutamine.
Täisarvu \(n\) faktoriaaliks nimetatakse korrutist \(n(n-1)(n-2)\ldots 2\cdot
1\) (märgime, et Mathcad'i korral pole tegelikult mõtet faktoriaali programmeerida,
sest faktoriaali annab avaldis n!). Kummaski
tsüklis võime loendurit alustada kohe 2-st, sest 1-ga korrutamine ei oma
mõtet.
.
Esimesse kastikesse kirjutatakse tõeväärtust omav avaldis, teise kastikesse
aga käsud, mille täitmist jätkatakse seni kuni selle avaldise tõeväärtus
muutub vääraks. Klassikaline näide kummagi tsükli kohta on faktoriaali arvutamine.
Täisarvu \(n\) faktoriaaliks nimetatakse korrutist \(n(n-1)(n-2)\ldots 2\cdot
1\) (märgime, et Mathcad'i korral pole tegelikult mõtet faktoriaali programmeerida,
sest faktoriaali annab avaldis n!). Kummaski
tsüklis võime loendurit alustada kohe 2-st, sest 1-ga korrutamine ei oma
mõtet.
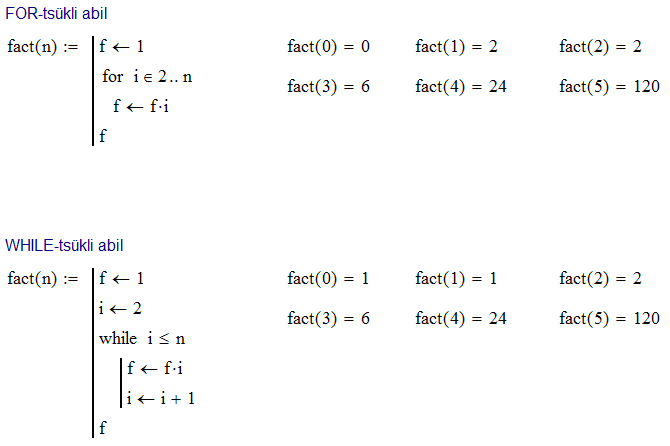
Nagu näha, funktsionaalselt sarnased FOR- ja WHILE-tsükkel erinevad vaid selle poolest, et WHILE-tsüklis tuleb ise hoolt kanda loenduri väärtuse muutmise eest, samas kui FOR-tsüklis toimub see automaatselt. Selles näites realiseeritud programmidel on siiski mõned puudused. Esiteks ei saa garanteerida, et funktsiooni fact kutsutakse välja vaid positiivse täisarvulise argumendiga; selle tingimuse täidetust tuleks kontrollida. Me võime leppida reaalarvulise argumendiga, mille funktsiooni round abil saaks ümardada lähima täisarvuni. Muutuja tüüpi saab Mathcad'is tuvastada funktsioonidega IsScalar, IsArray ja IsString. Need funktsioonid tagastavad väärtuse 1 (kui tõene) või 0 (kui väär). Reaalarvu kontrollimiseks tuleb lihtsalt tähele panna, et reaalarv on skaalar (kompleksarv), mille imaginaarosa on null. Imaginaarosa tagastab funktsioon Im. Alamprogrammi saab katkestada koos vastava veateate kuvamisega kasutades funktsiooni error. Veel üks potentsiaalne probleem on see, et definitsiooni kohaselt ka arvu null faktoriaal on võrdne 1-ga. Siin WHILE-tsükliga programm käitub korrektselt, kuid FOR-tsükliga programm annab väära tulemuse juba \(n=1\) korral, sest tsükli loendur omandab väärtused tagurpidises järjekorras: 2, 1 ja 0. Töökindlam funktsioon faktoriaali arvutamiseks oleks seega järgmine:

Siin oleme esmakordselt kombineerinud elementaarseid võrdlusoperatsioone kasutades loogilist liitmist ehk VÕI-tehet (operaator ∨) ning loogilist eitust (operaator ¬). Esimene on binaarne, teine aga unaarne operatsioon. Lisaks on olemas ka loogiline korrutamine ehk JA-tehe (operaator ∧). Kuivõrd Mathcad'is tõene on iga nullist erinev väärtus ja väär on nulliga võrdne väärtus, siis operaatori ∨ kasutamise efekt on tõeväärtuse arvutamise seisukohalt sama mis liitmine, ∧ efekt aga sama mis korrutamine. On siiski üks oluline põhjus, miks tasub liitmisele ja korrutamisele eelistada operaatoreid ∨ ja ∧. Oletagem, et toodud näites funktsioon fact kutsutakse välja sõne-tüüpi argumendiga. Sel juhul võib tekkida küsimus, et kas näiteks funktsiooni Im(n) väljakutsumine ei tekita omakorda viga, mida me ei näinudki ette? Selgub, et antud juhul seda ei juhtu, sest programmi täitmine selle operatsioonini üldse ei jõuagi. Nimelt sel juhul esimene test ¬IsScalar(n) annab kohe tõese tulemuse, aga loogiline liitmine on tõene niipea kui kasvõi üks operandidest on tõene, seega järgmiste operandide tõeväärtusi pole üldse mõtet välja arvutada. See on tavapärane käitumine enamikes programmeerimiskeeltes.
Juhul kui eesmärk on luua töökindlaid alamprogramme, mida oleks mugav korduvalt kasutada mitmetel erinevatel Mathcad'i töölehtedel, tuleks tähelepanu pöörata ka sellele, et massiivide indekseerimise algust määrava süsteemimuutuja ORIGIN väärtus võib erinevatel töölehtedel olla erinev (tavaliselt kas 0 või 1). Seega alamprogramm tuleks koostada nii, et see töötaks korrektselt sõltumata ORIGIN väärtusest. On ka mõeldav, et alamprogrammi poolt teostatav operatsioon sõltub sellest, millist tüüpi andmetega seda varustatakse. IsArray võimaldab kindlaks teha vaid seda, kas tegemist on mingit laadi massiiviga; massiivi dimensioonid saab seejärel leida juba funktsioonidega rows ja cols.
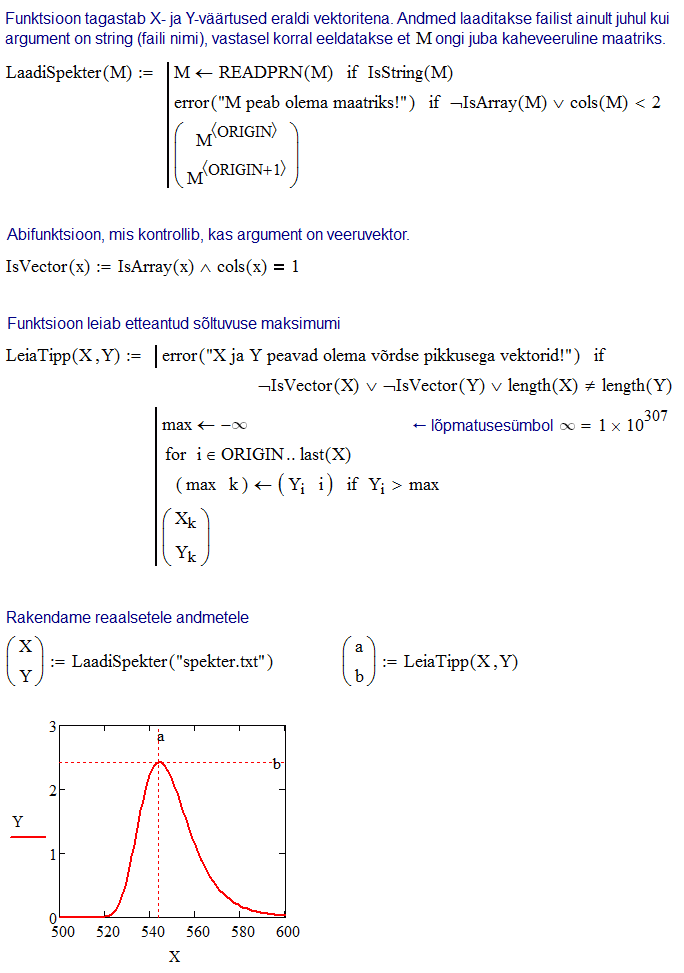
Selliste alamprogrammide loomise üks mõte on ka algoritmide lokaliseerimine. Näiteks äsjase nädisülesande puhul võib selguda, et mõne aja pärast õnnestub välja mõelda mõni parem meetod graafiku maksimumi leidmiseks; sel juhul tuleks vaid üks konkreetne alamprogramm välja vahetada, kogu töölehte ei pea aga detailselt läbi vaatama.
Nagu öeldud, võib FOR-tsükli loenduri diapasooni anda vektoriga. Lubatud on näidata diapasoonina ka mitu komaga eraldatud vektorit. Tuleb rõhutada, et sel juhul loenduri väärtusteks ei ole mitte vektorid ise, vaid endiselt elemendid vektorites. Järgnevas näites defineeritakse hulk infiks-operaatoreid hulgateoreetiliste avaldiste mugavaks kirjapanemiseks.

Sõnetöötlus
SisukordNagu mainitud, on string ehk sõne meelevaldsete sümbolite jada. Senistes näidetes on sõnedeks olnud vaid muutumatu väärtusega sõnekonstandid, mis sisestatakse jutumärkide vahele paigutatud tekstina. Aeg-ajalt on tarvilik ka sõnede programmiline loomine, muutmine või analüüs, st sõnetöötluse läbiviimine. Üldtuntud elementaaroperatsioonid sõnetöötlusel, mis on ka Mathcad'is toetatud, on sõne pikkuse leidmine (funktsioon strlen), kahe või enama sõne ühendamine (concat), alamsõne väljavõtmine (substr) ja teksti otsimine sõnest (search). Seda tüüpi operatsioone teostab ilmutatud kujul näiteks tavaline tekstiredaktor. Mitmete selliste operatsioonide juures on tarvis pöörduda individuaalsete sümbolite poole sõne koosseisus. Selleks peavad sümbolid sõnes olema ilmselt indekseeritud (täpselt samuti nagu elemendid massiivis). Mathcad'is sõne indekseerimine algab nullist, kui just ei ole aktiveeritud Tools → Worksheet Options → Calculation → Use ORIGIN for string indexing.
Vaatleme näitena olukorda, kus arvutuse lähteandmed laaditakse failist ja arvutuse tulemus salvestatakse samanimelisse, aga erineva laiendiga faili. Seejuures faili laiendi muutmine võiks toimuda automaatselt, nii et minimaalsete muudatustega saaks ühte ja sama arvutusskeemi rakendada mitmetele erinevatele andmefailidele.

Siin põhiline töö tehakse funktsioonis EemaldaLaiend, mis tagastab faili nime ilma laiendita. Alustades sõne lõpust, hakatakse sümbol-haaval otsima punkti failinimes. Juhul kui punkt leitakse, tagastatakse sellele eelnev osa failinimest. Kui aga jõutakse kurakaldkriipsuni (kataloogi eraldaja) või stringi algusesse, siis järelikult failinimel laiend puudub.
Kuigi sõnede korral ei ole matemaatilistest operatsioonidest mõtet rääkida, on siiski täiesti sisukas tegevus vaid numbrimärke sisaldava sõne konverteerimine vastavaks arvväärtuseks või arvu konverteerimine ekvivalentseks sõneks. Vastavad funktsioonid Mathcad'is on str2num ja num2str.
Sümbolarvutus
SisukordOma põhiolemuselt on
Mathcad ette nähtud numbriliste arvutuste teostamiseks, kuid ta suudab
vahendada käske ka arvutialgebrat (e. sümbolarvutust) võimaldavale
süsteemile (Maple
või
Mupad). See lubab Mathcad'i kasutada ka lihtsamate analüütiliste
teisenduste teostamiseks (avaldiste lihtsustamine, muutuja avaldamine võrrandist,
tuletise või integraali võtmine jms). Lihtsamal juhul piisab
muutujanime või avaldise selekteerimisest valides seejärel sobiliku
käsu menüüst Symbolics. Paindlikumaid
võimalusi pakub sümboolse arvutamise operaatori
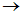 rakendamine (Ctrl+Shift+.).
Selle ette tekib kastike, kuhu võib kirjutada täiendavaid juhiseid
sümbolarvutuse protsessorile, näiteks simplify,
solve, substitute,
assume, series,
float jms. Ilma täiendavate märksõnadeta
teostatakse küll nõutud operatsioon (näiteks tuletise või integraali leidmine),
kuid täiendavaid teisendusi saadud avaldise lihtsustamiseks läbi ei viida.
Mitme märksõna sisestamiseks tuleb vajutada mitu korda
Ctrl+Shift+..
rakendamine (Ctrl+Shift+.).
Selle ette tekib kastike, kuhu võib kirjutada täiendavaid juhiseid
sümbolarvutuse protsessorile, näiteks simplify,
solve, substitute,
assume, series,
float jms. Ilma täiendavate märksõnadeta
teostatakse küll nõutud operatsioon (näiteks tuletise või integraali leidmine),
kuid täiendavaid teisendusi saadud avaldise lihtsustamiseks läbi ei viida.
Mitme märksõna sisestamiseks tuleb vajutada mitu korda
Ctrl+Shift+..

Rittaarenduse näidetega oleme reprodutseerinud hulga üldtuntud ligikaudse arvutamise valemeid: \((1+x)^n\approx 1+nx\), \(\cos(x)\approx 1-x^2/2\) jne, mis kehtivad tingimusel \(x\ll 1\).
Sümbolarvutuse sisuks on matemaatiliste avaldiste rangelt täpne teisendamine. Seetõttu vaid ratsionaalarvulisi konstante ja muutujaid sisaldava avaldise sümbolteisendus ei anna vaikimisi kunagi reaalarvulist tulemust, vaid vastus võib endiselt sisaldada hulganisti ratsionaalarve, matemaatilisi konstante (nagu \(\pi\) ja \(e\)) ja väljaarvutamata funktsioone. Küll aga saab märksõna float abil lasta tulemust aproksimeerida meelevaldse täpsusega reaalarvuga:

Mõistlike resultaatide saamine sümbolarvutusest eeldab mõnikord kasutajapoolset assisteerimist. Sümbolarvutuse käigus ei tehta vaikimisi mingeid eelduseid avaldises sisalduvate suuruste tüübi ja märgi kohta, st väärtustamata muutujad loetakse kompleksarvudeks. Enamasti on siiski teisendatava avaldise päritoluga (nt füüsikalise interpretatsiooniga) määratud avaldises sisalduvate muutujate iseloom, mida tuleks siis märksõnaga assume ka sümbolarvutuse protsessorile teada anda:

Võrrandid ja võrrandisüsteemid
SisukordÜldkujul \(f(x)=g(x)\) antud võrrandi lahendamine (st tundmatu \(x\) selliste väärtuste leidmine, mis rahuldab seda võrrandit) on ekvivalentne avaldise \(f(x)-g(x)\) nullkohtade leidmisega. Selleks otstarbeks on Mathcad'is funktsioon root. Selle saab välja kutsuda kujul root(f(x)-g(x), x, a, b), kus lahend eeldatakse olema lõigus \([a,b]\). Seega ilmselt \(f(a)-g(a)\) ja \(f(b)-g(b)\) peavad olema erimärgilised. Funktsiooni root võib välja kutsuda ka lihtsamal kujul root(f(x)-g(x), x), aga sel juhul tuleb eelnevalt omistada \(x\)-ile alglähend (guess value).
Võrrandi numbrilist lahendamist läheb tarvis näiteks transtsendentsete võrrandite korral, millest tundmatut ei ole võimalik analüütiliselt avaldada. Vaatleme näitena absoluutselt musta keha kiirguse spektrit \(f(\lambda)\propto x^5/(e^x-1)\), kus \(x\equiv hc/\lambda k T\). Leiame, millisel lainepikkusel on kiirgus kõige intensiivsem. Funktsiooni maksimumis on selle tuletis võrdne nulliga, \(df(\lambda)/d\lambda=0\) ehk \(e^{-x}+x/5-1=0\). Viimast võrdust rahuldava \(x\) väärtuse saab leida ainult numbriliselt.
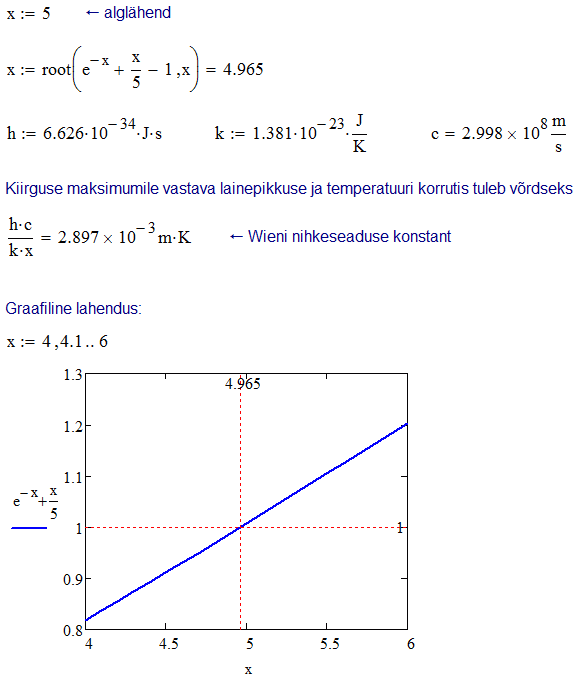
Nii lineaarsete kui ka mittelineaarsete võrrandite süsteemi numbriliseks lahendamiseks saab kasutada funktsiooni Find. Selleks tuleb koostada nn lahendusplokk (solve block). Esmalt tuleb sisestada võtmesõna Given, millele järgnevad kõik võrrandid (viimaste üleskirjutamisel tuleb mõistagi kasutada "rasvast" võrdusmärki). Lahendusploki lõpetab funktsiooni Find väljakutse. Funktsiooni Find argumentideks on kõigi otsitavate muutujate nimed ja funktsioon tagastab vastavate väärtuste vektori. Enne funktsiooni Find väljakutset peavad olema antud ka kõigi tundmatute alglähendid. Järgnev näide leiab sellise parabooli \(y=ax^2+bx+c\), mis läheb täpselt läbi etteantud kolme punkti \((x_1,y_1)\), \((x_2,y_2)\) ja \((x_3,y_3)\).
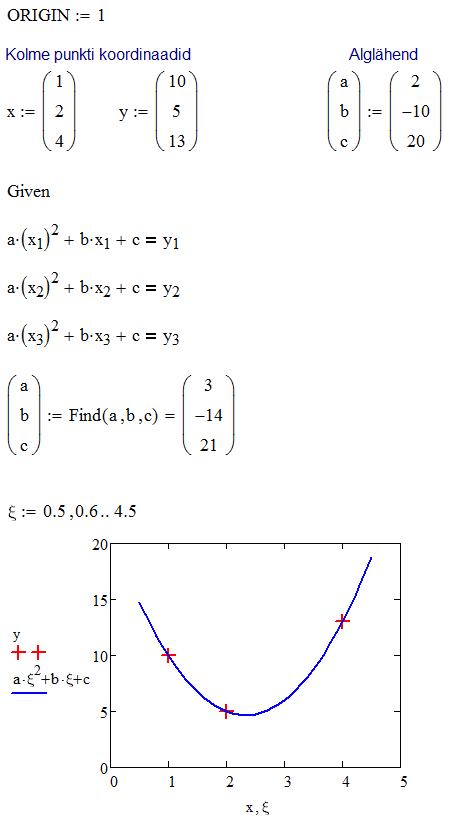
Antud juhul on tegemist lineaarse võrrandisüsteemiga, mille lahendamiseks on ka rida sirgjoonelisemaid teid. Sellise lineaarse võrrandisüsteemi saab esitada kujul \(Mp=y\), kus \[M=\begin{bmatrix} (x_1)^2 & x_1 & 1\\ (x_2)^2 & x_2 & 1\\(x_3)^2 & x_3 & 1\end{bmatrix},\quad p=\begin{bmatrix} a\\ b\\c\end{bmatrix}, \quad y=\begin{bmatrix} y_1\\ y_2\\y_3\end{bmatrix}.\] Põhimõtteliselt on sellise võrrandisüsteemi lahend esitatav pöördmaatriksi kaudu: \(p=M^{-1}y\). Mathcad'is on siiski olemas ka spetsiaalne funktsioon lineaarsete võrrandisüsteemide lahendamiseks, lsolve(M,y), mis on kiirem ja täpsem (näiteks juhul kui maatriks \(M\) on peaaegu singulaarne).
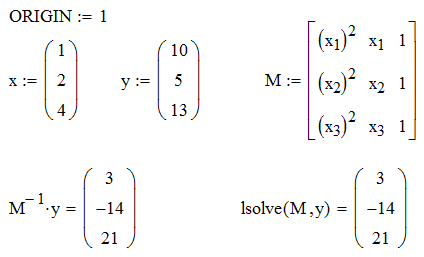
Nii funktsiooni Find kui ka lsolve saab välja kutsuda sümbolarvutuse võtmes, mis võimaldab leida võrrandisüsteemi analüütilise lahendi. Juhul kui lahendeid on mitu, väljastatakse need maatriksina, mille iga veeruvektor esitab ühe lahendi.

Funktsioonide sobitamine ja matemaatiline optimeerimine
Sisukord Tüüpiline numbriline arvutusprobleem
loodus- ja inseneriteadustes on teooria "sobitamine" katseandmetega,
st teoreetilises mudelis sisalduvate vabade parameetrite timmimine kuni
mudel on "parimas kooskõlas" eksperimendiga. Kui eksperimentaalne
sõltuvus on antud katsepunktidena \((x_i,y_i)\) ja mudeli kohaselt peaks
\(x\) ja \(y\) vahel olema seos \(y=f(x,a,b,\ldots)\), siis
vähimruutude
mõttes parim kooskõla saavutatakse parameetrite \(a,b,\ldots\)
selliste väärtuste korral, mis minimeerib erinevuse \(\sum_i [y_i-f(x_i,a,b,\ldots)]^2\).
Lihtsaim mudel on lineaarne seos \(y=ax+b\), mis on õnneks ka üsna levinud.
Lineariseerige harjutuseks järgmised sõltuvused:
\(y=a/x\)
\(y=ae^{-bx}\)
\(y=ax^b\)Mõningad muud lihtsad mudelid (astmefunktsioon, eksponentfunktsioon)
on jällegi võimalik esitada sellistes koordinaatides, kus seos muutub lineaarseks.
Kui eksperimentaalne sõltuvus (katsepunktid) on Mathcad'is esitatud vektoritena
X ja Y, siis vähimruutude
mõttes parima lähendussirge tõusu \(a\) tagastab funktsioon
slope(X,Y), algordinaadi \(b\) aga
intercept(X,Y). Mõlemad parameetrid
korraga tagastab line(X,Y).
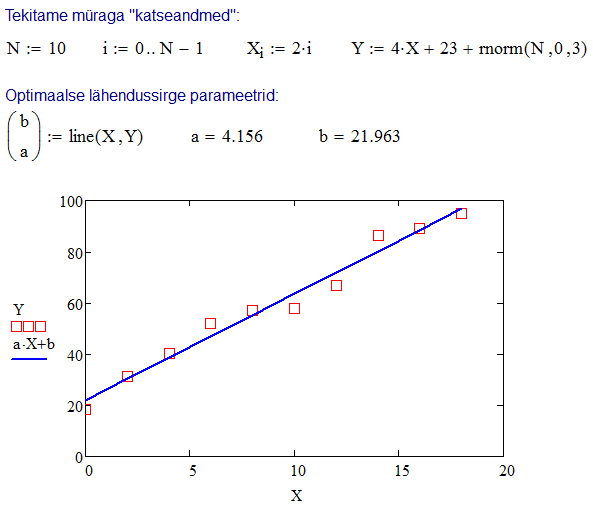
Lineaarsõltuvuse erivariant on proportsionaalne sõltuvus \(y=ax\), st regressioonsirge peab tingimata läbima koordinaatide alguspunkti \((x=0, y=0)\). Lihtne arvutus näitab, et vähimruutude mõttes parima regressioonsirge tõus on sel juhul \(a=\frac{\sum_i x_i y_i}{\sum_i x_i^2}\). Selle saab Mathcad'is mugavalt kirja panna vektorite skalaarkorrutise kaudu, ilma summamärki kasutamata:
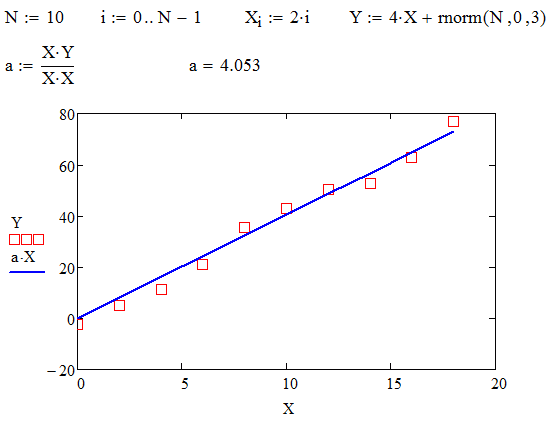
Isegi kui füüsikaline mudel ei ole teada (või on liiga keeruline), on
sageli võimalik ja õigustatud suure müraga katselise sõltuvuse
siledaks aproksimeerimiseks kasutada mingit piisavalt paindlikku matemaatilist
funktsiooni, millel füüsikalist põhjendust ei pruugi olla. Selline funktsioon
on näiteks polünoom \(f(x)=a_0+a_1x+a_2x^2+\ldots\).
Polünoomi saab vaadelda kui teatud lihtsate baasfunktsioonide
lineaarkombinatsiooni. Samas baasfunktsioonideks ei pea tingimata
olema vaid astmefunktsioonid \(x^n\). Selgub, et mistahes kindlatest baasfunktsioonidest
koostatud lineaarkombinatsiooni sobitamine katseandmetega (vähimruutude
mõttes) on matemaatiliselt hästi defineeritud ja ühese lahendusega ülesanne,
st eksisteerivad lihtsad analüütilised valemid lineaarkombinatsiooni optimaalsete
kordajate leidmiseks. Mathcad'is need valemid realiseerib funktsiooni
linfit.
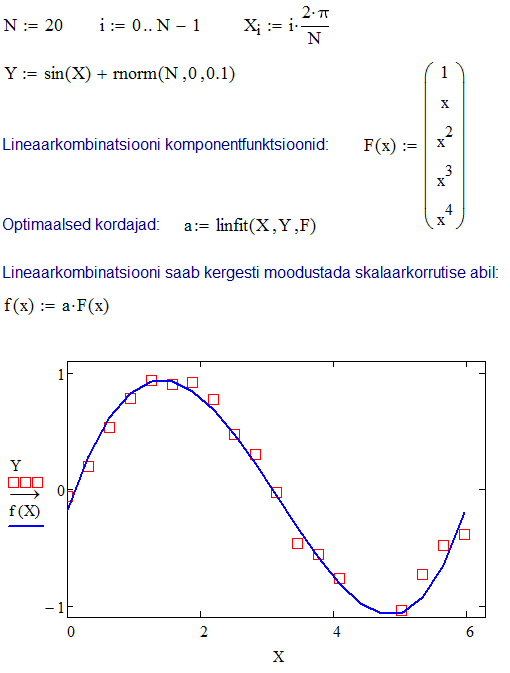
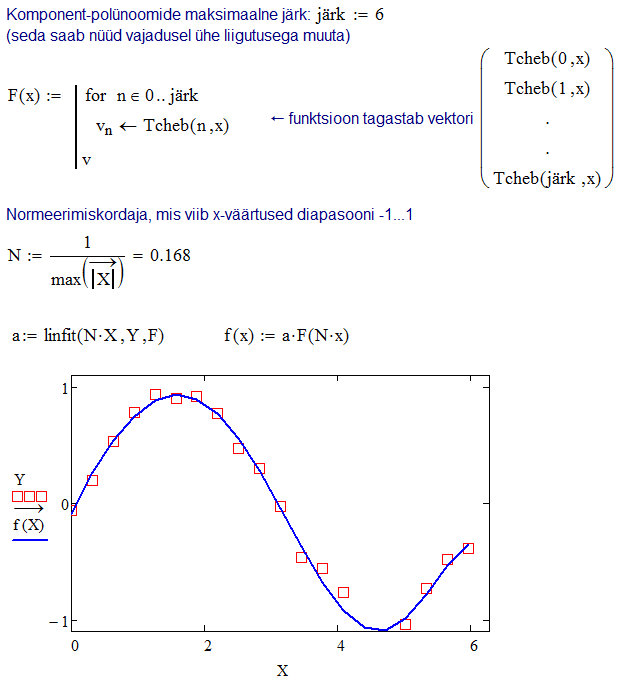
Toodud näide sisaldab mõningaid potentsiaalseid probleeme. Esiteks, astmete baasil moodustatud lineaarkombinatsioon ei ole numbriliselt stabiilne, st väikesed muutused või vead kordajates või argumendi \(x\) väärtuses mõjutavad tugevasti lineaarkombinatsiooni väärtust. Selles mõttes sobivad baasfunktsioonideks palju paremini näiteks Tsebõsevi polünoomid. \(n\)-ndat järku Tsebõsevi polünoomi väärtuse kohal \(x\) tagastab Mathcad'i funktsioon Tcheb(n,x). Teiseks, arvutuste stabiilsust parendaks ka see, kui normeerida \(x\) väärtused diapasooni –1…1. Kolmandaks, toodud näites on tülikas muuta polünoomi järku: selleks tuleb redigeerida funktsiooni F(x). Järgnevas variandis on kõik need puudused kõrvaldatud.
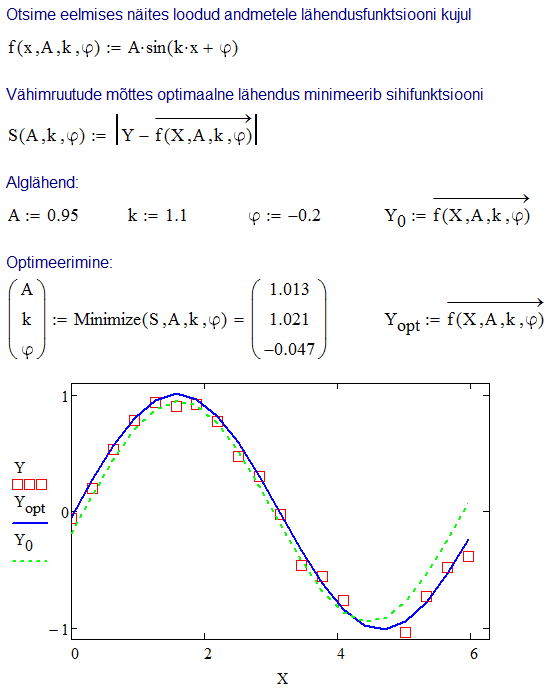
Üldjuhul kõige lihtsam tee mittelineaarsete funktsioonide sobitamiseks
on kasutada funktsioone Minimize või
Minerr. Erinevalt lineaarkombinatsiooni sobitamisest
ei ole sel juhul lahendus ühene, seega tuleb ette anda ka otsitavate
parameetrite võimalikult täpsed alglähendid.
Funktsioonid Minimize ja
Maximize on otseselt ette nähtud
planeerimis- ja optimeerimisülesannete
lahendamiseks. Sellistes ülesannetes püstitatakse
sihifunktsioon (mille väärtus on tarvis kas minimeerida või maksimeerida),
millega kaasnevad sageli ka täiendavad kitsendused
võrrandite või võrratuste kujul. Viimased tuleb Mathcad'is kirjutada võtmesõnaga
Given tähistatud lahendusplokki. Vaatleme näitena
mõnevõrra kunstlikku ülesannet, mis on nii triviaalne, et tavaliselt seda
optimeerimisülesandena ei käsitleta: milliste maksimaalsete mõõtudega saab
pildi algsuurusega 100×66 mm trükkida A4 paberilehele (297×210
mm)? Siin võib sihifunktsiooniks võtta mistahes mõõdu, mis iseloomustab
pildi suurust.

Funktsioon Minerr on ette nähtud võrrandite/võrratuste süsteemi nii-öelda ligikaudseks lahendamiseks. Minerr (Minimize Error) püüab lahendi leidmisel samm-sammult vähendada üleüldist viga, kus kõiki Given-plokis esinevaid kitsendusi võetakse arvesse võrdse kaaluga. Saadud tulemus tagastatakse ka juhul kui täpset lahendit ei õnnestu leida. See lubab funktsiooni Minerr kasutada ka funktsioonide sobitamiseks, mille puhul seatakse tingimuseks, et katsepunktide ja mudeli erinevust iseloomustav karakteristik oleks võrdne nulliga. Funktsiooni Minerr korral on võimalik kasutada populaarset Levenberg–Marquardt'i optimeerimisalgoritmi (kontekstimenüüst Nonlinear → Levenberg–Marquardt). Seejuures on lubatud vektorvõrrandite ja -võrratuste kasutamine, kusjuures tagastatud tulemus on ekvivalentne optimumiga vähimruutude kriteeriumi mõttes. See tähendab ühtlasi, et mudeli ja katsepunktide erinevuste ruutude summat pole tarvis ise konstrueerida — piisab kui vastav vigade vektor seada võrdseks nulliga. Seega üle-eelmise näite saab realiseerida Minerr abil järgmiselt:
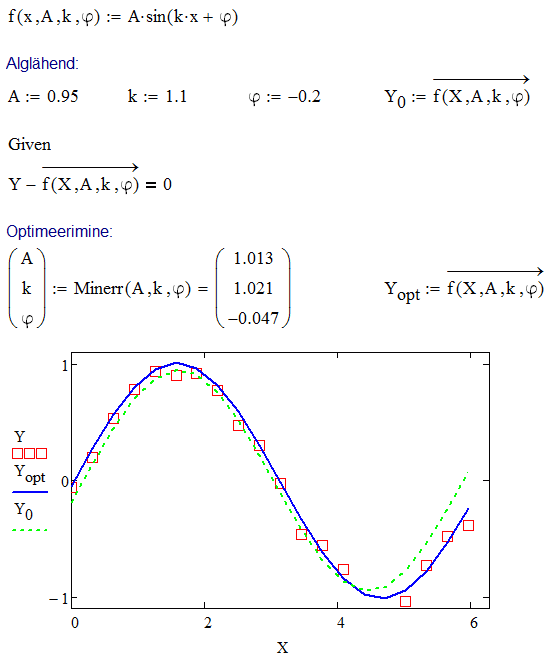
Interpoleerimine
SisukordKuna mistahes eksperimentaalne sõltuvus võetakse paratamatult üles lõpliku sammuga, võib tekkida vajadus mõõdetava suuruse väärtuse hindamiseks ka katsepunktide vahel. Juhul kui teoreetiline sõltuvus \(x\) ja \(y\) vahel on teada (ja piisavalt lihtne), kasutatakse funktsiooni sobitamist nagu kirjeldatud eespool. See on eriti eelistatud juhul kui katseandmed on suure määramatusega ehk "mürased". Muudel juhtudel kasutatakse interpoleerimist, st konstrueeritakse katsepunkte ühendav (võimalikult sile) kõver, millel füüsikalist põhjendust ei pruugi olla. Kuivõrd interpoleeritud kõver (erinevalt lähendusfunktsioonist) läbib täpselt kõiki katsepunkte, peavad viimased olema piisavalt väikese veaga.
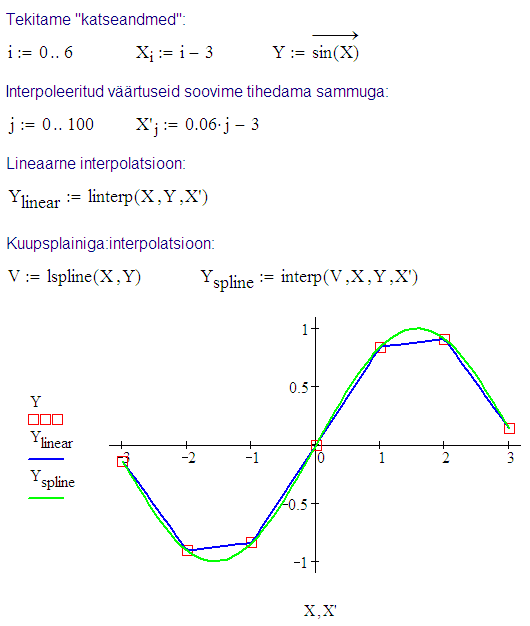
Kõige soodsam olukord interpoleerimiseks on juhul, kui katsepunktid
paiknevad väga tihedalt või on muutused väga aeglased.
Sel juhul on õigustatud lineaarne interpolatsioon, st naabersõlmed ühendatakse
sirgjoonega. Mathcad'is saab lineaarselt interpoleeritud \(y\)-väärtuse
kohal \(x\) leida avaldisega linterp(X,Y,x).
Üldjuhul kasutatakse katsepunkte läbiva sileda kõvera
konstrueerimiseks enamasti kuupsplaini. Viimane
koosneb tükati kuuppolünoomidest, mis on sõlmpunktides
võimalikult siledalt kokku seotud (matemaatilistes terminites: esimene
ja teine tuletis on sõlmpunktides pidevad). Esmalt tuleb tekitada
vektor V, mis sisaldab splaini teise tuletise
väärtusi sõlmpunktides. Selleks saab kasutada ühte
kolmest funktsioonist: lspline(X,Y),
pspline(X,Y) või
cspline(X,Y). Nimetatud funktsiooni valik määrab,
kas splain on otspunktides lineaarne, parabool või kuupparabool,
st põhiliselt mõjutab see ekstrapolatsiooni iseloomu. Seejärel
interpoleerimine ise toimub avaldisega interp(V,X,Y,x),
mis arvutab interpoleeritud \(y\)-väärtuse kohal \(x\).
Olgu märgitud, et kõik interpoleerimisalgoritmid eeldavad lähteandmete sorteeritust \(x\) väärtuste järgi. Selle probleemi lahendamiseks võib kasutada funktsiooni csort (või erijuhul funktsiooni reverse).
Diferentsiaalvõrrandid
SisukordHarilike diferentsiaalvõrrandite süsteem on esitatav kujul \[\begin{cases} \frac{dy_1}{dx}=f_1(x,y_1,y_2,\ldots)\\ \frac{dy_2}{dx}=f_2(x,y_1,y_2,\ldots)\\ \quad\vdots \\ \frac{dy_N}{dx}=f_N(x,y_1,y_2,\ldots)\end{cases},\] kus \(x\) on sõltumatu muutuja (näiteks aeg), \(y_1,y_2,\ldots, y_N\) on sõltuvad muutujad (näiteks läbitud teepikkus vms) ja \(f_1,f_2,\ldots,f_N\) on teadaolevad funktsioonid. Sõltuvaid muutujaid võib vaadelda vektorina \(y=(y_1,\ldots,y_N)\), samuti funktsioonid \(f_1,\ldots,f_N\) võib kokku võtta ühte vektorfunktsiooni \(f\), nii et terve võrrandisüsteemi saab esitada üheainsa vektorvõrrandiga \(dy/dx=f(x,y)\). Diferentsiaalvõrrandite süsteemiga kaasnevad ka algtingimused kujul \(y(x_0)=y_0\).
Ka üksik, kõrgemaid tuletisi sisaldav harilik diferentsiaalvõrrand on esitatav eeltoodud kujul. Näiteks harmoonilise liikumise võrrand \(d^2x/dt^2=-\omega^2x\) teiseneb süsteemiks \[\begin{cases} \frac{dv}{dt}=-\omega^2x,\\ \frac{dx}{dt}=v\end{cases},\] kus sõltuvad muutujad on tähistatud \(x\) ja \(v\) (koordinaat ja kiirus).
Selliste diferentsiaalvõrrandite süsteemi numbriliseks lahendamiseks on välja mõeldud rida algoritme. Enamasti sõltumatu muutuja diapasoon jagatakse piisavalt väikesteks vahemikeks sammuga \(h\) ja sõltuvate muutujate väärtused arvutatakse järk-järgult punktides \(x_n=x_0+nh\), kus \(n=0,1,2,\ldots\), alustades algtingimusega antud väärtusest \(y(x_0)=y_0\). Kõige lihtsam ja äärmiselt ebaefektiivne meetod on Euleri meetod, mille puhul \(y_{n+1}=y_n+hf(x_n,y_n)\). Saab aga välja mõelda meetodeid, mis on küll keerukamad, aga hulga efektiivsemad selles mõttes, et sammu \(h\) ei pea tegema väga väikeseks. Tuntud fikseeritud sammuga meetod on näiteks 4-ndat järku Runge-Kutta meetod. Eksisteerib ka meetodeid, kus sammu suurust jooksvalt varieeritakse sõltuvalt lahendi muutumise kiirusest. Kõigi seda tüüpi meetodite rakendamiseks on Mathcad'is rida funktsioone, millest sobivaim tuleb valida vastavalt diferentsiaalvõrrandite iseloomule. Näiteks fikseeritud sammuga 4-ndat järku Runge-Kutta meetodi realiseerib funktsioon rkfixed, varieeruva sammuga aga funktsioon Rkadapt. Kõigi nende funktsioonide väljakutsumine toimub valdavalt ühesugusel viisil, näiteks rkfixed(y0, x0, xmax, intvls, f), kus sõltumatu muutuja diapasoon alates x0 kuni xmax on jagatud intvls osaks, y0 on algväärtuste vektor ja f on eelpoolkirjeldatud vektorfunktsioon, mis sisuliselt defineerib kogu diferentsiaalvõrrandite süsteemi. Funktsioonid rkfixed, Rkadapt, jne tagastavad intvls+1 realise maatriksi, mille esimeses veerus on sõltumatu muutuja väärtused ja järgmised veerud sisaldavad sõltuvate muutujate vastavaid väärtuseid.
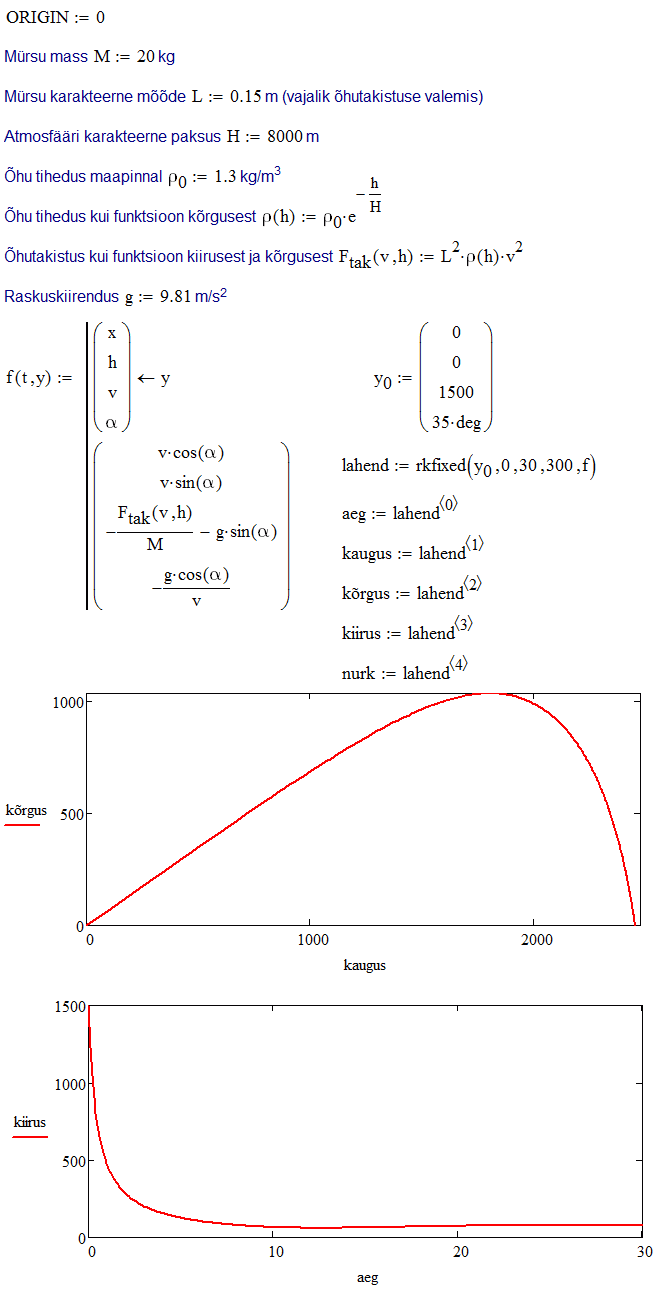
Vaatleme näitena mürsu ballistilist liikumist, kus võetakse arvesse ka õhutakistust. Siin sõltumatuks muutujaks on aeg \(t\), sõltuvateks muutujateks on aga kaugus \(x\), kõrgus \(h\), kiirus \(v\) ning kiirusvektori ja horisontaalsihi vaheline nurk \(\alpha\). Newtoni seaduste abil saame mürsu liikumise kirjeldamiseks diferentsiaalvõrrandite süsteemi \[\begin{cases} \frac{dx}{dt}= v\cos\alpha\\ \frac{dh}{dt}= v\sin\alpha\\ \frac{dv}{dt}= -\frac{F_\text{tak}}{M}-g\sin\alpha \\ \frac{d\alpha}{dt}=-\frac{g\cos\alpha}{v} \end{cases}, \] kus \(g\) on raskuskiirendus, \(M\) on mürsu mass ja \(F_\text{tak}\) on õhutakistus. Viimase loeme võrdeliseks kiiruse ruuduga ja õhu tihedusega. Märgime, et ühikute kasutamine antud näites on tülikas, sest funktsioon \(f\) peab tagastama vektori, aga Mathcad ei luba ühte massiivi asetada erinevate ühikutega väärtusi. Seega lepime lihtsalt kokku, et kõik suurused on SI põhiühikutes. Katse-eksituse meetodil võib veenduda, et kasutatavate simulatsiooni parameetrite korral on lennu kestus veidi alla 30 s. Kui nõuda ajasammuks 0.1 s, siis tuleb ajavahemik 0 kuni 30 s jagada 300-ks osaks.
Pilditöötlus
SisukordKaks tuntud näidet digitaalsetest andmetest, mis on kirjeldatavad homogeensete (ja sageli üsna mahukate) arvumassiividena, on rastergraafika ja helifailid. Rastergraafika pilt on vaadeldav ühe või mitme maatriksina (vastavalt primaarvärvuste arvule), helifail aga ühe või mitme vektorina (vastavalt kanalite arvule). Siinkohal vaatleme vaid pilditöötlusega seonduvat.
Rastergraafikas moodustub kujutis väikestest ühetaolistest pildielementidest ehk pikslitest. Seega kahemõõtmeline kujutis on aproksimeeritav kui pikslite maatriks. Sõltuvalt sellest kui palju mälu iga piksli värvuse kodeerimiseks hõivatakse, saab rääkida monokroomsetest, halltoonides ja värvilistest rasterkujutistest. Halltoonides pildi korral salvestatakse vaid piksli heledus, värvusinfo läheb kaotsi. Tavaliselt reserveeritakse igale pikslile üks bait mälu, seega piksli heledus väljendub täisarvuna vahemikus 0…255 (baidis on kaheksa bitti, seega maksimaalne väärtus on 28–1=255). Mathcad'is saab halltoonides kujutise (*.bmp, *.jpg või *.gif faili) maatriksina sisse lugeda funktsiooniga READ_IMAGE, mis võtab argumendina faili nime. Pildi kuvamiseks töölehel tuleb kasutada nn. pildioperaatorit, mis tekib menüükäsuga Insert → Picture. Pildina interpreteeritava maatriksi väärtused ei pea olema küll täisarvud (Mathcad'is ei olegi täisarvulist andmetüüpi), kuid võiksid jääda diapasooni 0–255. Sellele tuleb tähelepanu pöörata siis, kui pildimaatriksiga teostatakse matemaatilisi operatsioone (pildi heleduse või kontrasti muutmine vms).

Selles näites toodud pilditöötlusoperatsioonid seisnevad eraldi iga piksli heleduse timmimisel. Niimoodi saab muuta pildi heledust, kontrasti, jne. Täiendavad võimalused (näiteks kujutise teravustamine, müravähendus jpt) nõuavad juba erinevate pikslite heleduste kombineerimist. Sageli see operatsioon seisneb lihtsalt naaberpikslite heleduste kaalutud summa leidmises. Sel juhul saab defineerida vastava maatriksi, mis näitab, millise kaaluga tuleb piksli ja tema kõigi naaberpikslite heledusi arvesse võtta. Kui piirduda ainult lähimate naabritega, siis selle maatriksi suurus on ilmselt 3×3.

Värvilise kujutise korral kõik silmaga tajutavad värvitoonid aproksimeeritakse kolme primaarvärvuse — punase, rohelise ja sinise — kombinatsioonina. Sellist kujutist kirjeldab seega kolm arvumaatriksit. Värvilise kujutise saab Mathcad'i lugeda funktsiooniga READRGB, mis tagastab vaid ühe suure maatriksi, kus eelpool nimetatud kolm primaarvärvuste heleduste maatriksit on kõrvuti kokku pandud (järjestuses punane, roheline, sinine). Funktsiooni submatrix abil saab need üksteisest eraldada. Et pildioperaatoriga kuvada värviline kujutis, tuleb sellele ette anda kõik kolm komponentmaatriksit.

Töödeldud pildi saab vajadusel uuesti salvestada bitmap-formaadis (*.bmp) kasutades funktsioone WRITEBMP (halltoonides) või WRITERGB (värviline). Viimasel juhul tuleb mõistagi pildimaatriks kokku panna kolmest primaarvärvuste maatriksist (kasutades näiteks funktsiooni augment).
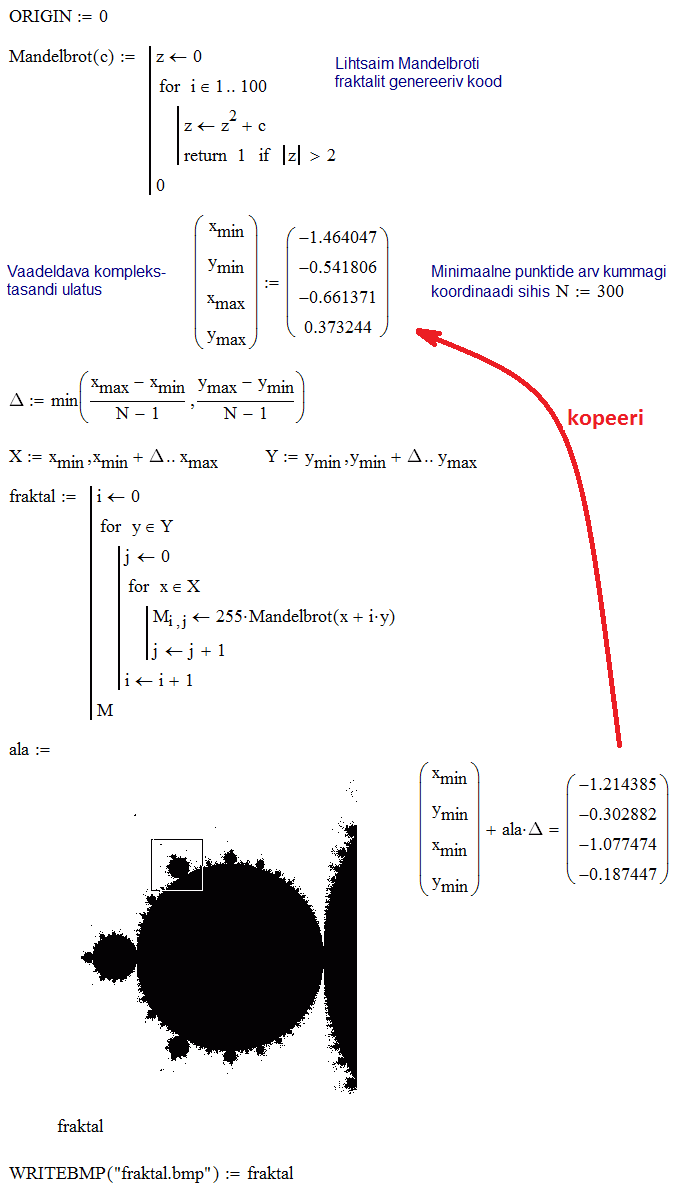
Rasterkujutisena tõlgendatava maatriksi võib muidugi ka puht matemaatiliselt konstrueerida. Selles mõttes pildioperaator on lihtsalt üks alternatiivne viis värviskaalas 3D-graafiku näitamiseks. Piltioperaatoril on ka teatud kasulikke võimalusi, mida tavalised 2D- või 3D-graafikud ei oma. Näiteks saab hiirega selekteerida teatud punkti või ristküliku-kujulise ala ja väljastada selle koordinaadid (pikslites). Selleks tuleb pildioperaatori kontekstimenüüst valida Properties ja märgistada valik Output Selected Coordinates. Järgnevas näites kasutatakse neid võimalusi selleks, et mugavalt suurendada teatud piirkonda Mandelbroti fraktalist.
Animatsioonid
SisukordAnimatsiooniks nimetatakse antud kontekstis videot, mis kirjeldab arvutustulemuse (harilikult graafiku) muutumist sõltuvana arvutuse mingi parameetri süstemaatilisest varieerimisest. Nimetatud parameeter seotakse süsteemimuutujaga FRAME, mille iga väärtus tekitab ühe videokaadri. Esmalt tuleb koostada muutujat FRAME sisaldav arvutus:
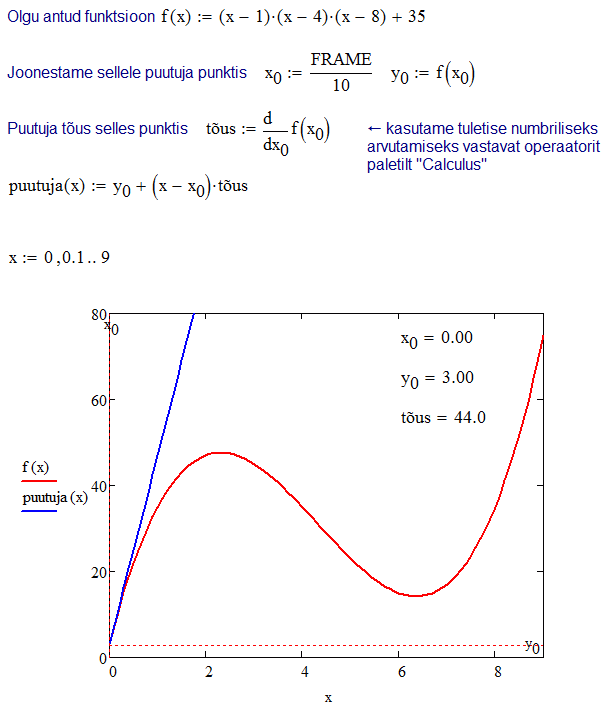
Seejärel tuleb avada animatsiooni salvestamise dialoog käsuga Tools → Animation → Record… ja seada muutuja FRAME algus- ja lõppväärtus ning kaadrite arv sekundis. Antud näites on need väärtused vastavalt 0, 90 ja 10, nii et animatsiooni kestus saab olema 9 sekundit. Viimaks tuleb selekteerida hiirega töölehel ristkülikukujuline piirkond, milles toimuvat soovitakse salvestada, ja vajutada nupule Animate. Saadud animatsiooni saab salvestada vajutusega nupule Save As…. Käesoleva näite animatsioon on laetav siit. Veel näiteid animatsioonidest: lainete murdumine, mürsu ballistiline liikumine, game of life.
Kiiruse ja mäluvajaduse optimeerimine
SisukordKuigi Mathcad ei ole traditsiooniline kompileeritav programmeerimiskeel (nagu Pascal vms), jäävad ka siin mahukate arvutuste optimeerimisel kehtima teatud elementaarsed põhimõtted ja lisanduvad mõned, mis on spetsiifilised vaid Mathcad'ile. Eelnevas on mõningaid ideid juba möödaminnes mainitud. Enne vastavate põhimõtete sõnastamist oleks meil tarvis mugavat võimalust arvutuskiiruse testimiseks. Selleks pakub Mathcad funktsiooni time, mis tagastab arvuti kella näidu sekundites. Selle funktsiooni kahe järjestikuse väljakutsega saab arvutada kahe ajahetke erinevuse, mida ongi tarvis arvutuse kestuse mõõtmiseks. Mathcad'i süntaksi eripära tõttu iga funktsioon vajab vähemalt ühte argumenti, mis funktsiooni time korral võib olla suvaline. Funktsioon time koos testimisele kuuluva koodiga käivitatakse tavaliselt alamprogrammi sees. Tuleb muidugi arvestada, et kõik lihtoperatsioonid üksikute skaalarite või väikeste vektorite/maatriksitega on tajutavate/mõõdetavate ajamastaapidega võrreldes ülikiired ja mingisugusegi märgatava viivise saamiseks tuleb selliseid operatsioone korrata suure hulga andmetega. Testimise ajal ei tohiks muid aktiivseid protsesse arvutis joosta.
Kordamiste vältimine
Olgu meil antud funktsioon \(f(x)=2\sqrt{\frac{\ln 2}{\pi}}\exp[-4\ln(2)x^2]\). See on Gaussi ehk Doppleri profiili teatav standardiseeritud kuju, mille pindala on 1 ja laius poolel kõrgusel samuti 1. Sellest tulenevalt sisalduvad funktsiooni definitsioonis mitmesuguste matemaatiliste konstantide kombinatsioonid [vastasel korral oleksime võinud võtta lihtsalt funktsiooni \(f(x)=\exp(-x^2)\)]. Kui seda funktsiooni sellisel kujul kasutada, siis funktsiooni igal väljakutsel peab arvuti uuesti teostama kõik matemaatilised operatsioonid ka kõigi algusest peale teadaolevate arvude vahel. Selle vältimiseks võib kõik teadaolevate arvväärtuste kombinatsioonid juba eelnevalt välja arvutada ja asendada vastava reaalarvuga (mõnes mõttes muidugi kannatab koodi loetavus).

Saime ligi kahekordse võidu kiiruses. Tegelikult Mathcad suudab seda laadi optimeerimist ka ise organiseerida. Kui piirkonna kontekstimenüüst valida Optimize, siis laseb Mathcad sümbolarvutuse protsessoril avaldist optimeerida. Kuid nagu juba öeldud, ainult täisarve või matemaatilisi konstante (π) sisaldava avaldise korral hõlmab sümbolarvutus ainult täpseid teisendusi. Et anda sümbolarvutuse süsteemile mõista ka ligikaudsete reaalarvuliste arvutuste lubatavust, tuleks vähemalt mõned arvväärtused avaldises esitada reaalarvuna, näiteks antud juhul ln(2) asemel kirjutada ln(2.0). Kui avaldise optimeerimine õnnestub, siis avaldis märgistatakse punase tärnikesega ning avaldise optimeeritud kuju (mida Mathcad edasistes arvutustes hakkab kasutama) saab näha valides kohtmenüüst Show Optimization. Antud juhul optimeeritud avaldis on isegi mõnevõrra kiirem kui käsitsi sisestatud variant.
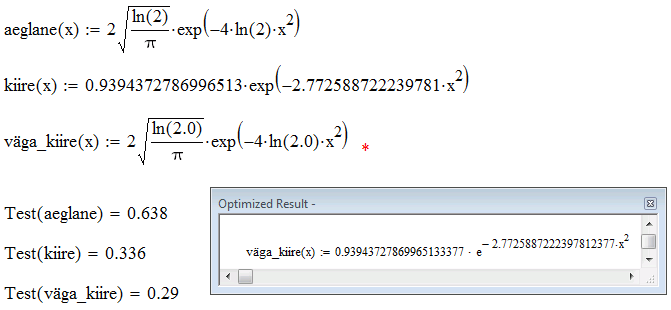
Mõningate matemaatiliste funktsioonide defineerimisel võimaldab alamprogrammide kasutamine saavutada suurema arvutuskiiruse tänu sellele, et funktsiooni avaldises mitu korda esineva operatsiooni saab eraldi välja arvutada ja säilitada vahetulemusena lokaalses muutujas. Sel juhul ka koodi loetavus sageli paraneb, sest tuleb selgemalt esile matemaatilise avaldise või algoritmi struktuur. Vaatleme seda funktsiooni \(f(x)=(x/\pi)^2\exp[-(x/\pi)^2]\) näitel.
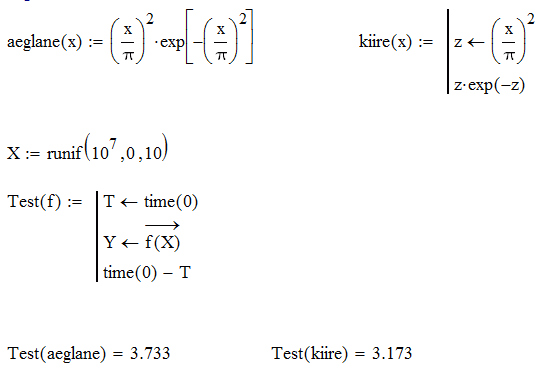
Antud näite korral on kiiruste erinevus siiski marginaalne, sest teatud aeg kulub protsessoril ka alamprogrammis esineva lokaalse muutuja z kasutuselevõtuks.
Mälu ette tellimine suurtele massiividele
Mathcad'is on kõik massiivid dünaamilised, st massiivile allokeeritud mälu suurendatakse vajadusel automaatselt elementide lisandudes. Skalaarse väärtuse säilitamine arvuti mälus nõuab teatud arvu mälupesi (ütleme näiteks \(n\) tükki). Järelikult \(M\times N\) elemendist koosneva arvumassiivi säilitamine nõuab \(M\times N\times n\) järjestikust vaba mälupesa. Kui nüüd omistada väärtus viimase elemendi indeksist suurema indeksiga elemendile, siis arvuti on sunnitud otsima või organiseerima veel suurema vaba sidusa mälupiirkonna ja kopeerima vanast massiivist kõik elemendid üle. See protseduur võib suuremate massiivide korral kulutada võrdlemisi palju aega. Juhul kui massiivi lõplik suurus on ette teada, saab kogu vajaliku mälu reserveerida kohe, omistades suvalise väärtuse massiivi viimasele elemendile. Siiski, nagu järgnev näide demonstreerib, hakkab probleem väga järsult ilmnema alles teatud piiridest suuremate massiivide korral.
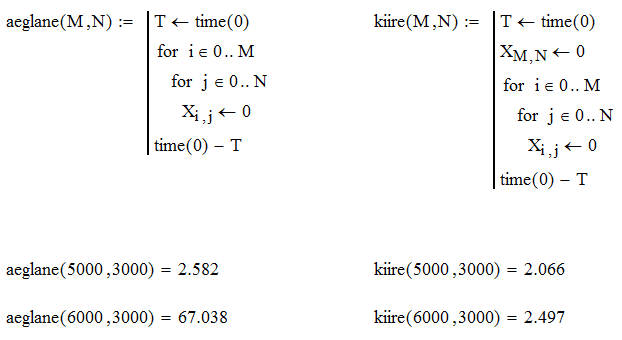
Vektoriseerimine (või selle vältimine)
Vektoriseerimisoperaator avaldise kohal annab Mathcad'ile mõista, et kui avaldises sisalduvad massiivid, siis tuleb arvutus teostada tingimata element-kaupa, st mitte hakata tõlgendama maatriks- ja vektoroperatsioone lineaaralgebra või mõnes muus spetsiifilises tähenduses. Sel juhul mõistagi kõik avaldises sisalduvad massiivid peavad olema ühesuguste mõõtmetega ja arvutuse tulemuseks on samade mõõtmetega massiiv. Juhtudel, kus vektoriseerimine on vajalik ja võimalik, annab ta harilikult kiirema koodi kui indeksitega arvutamine ja samas võimaldab avaldised ka lihtsamalt ja elegantsemalt kirja panna.
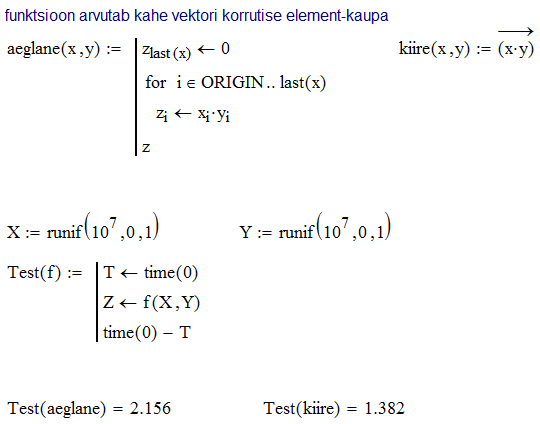
Vektoriseerimisoperaator on tarvilik vaid siis kui Mathcad võib valesti aru saada sellest, mida teha tahetakse (nagu eelnevas näites, kus ilma vektoriseerimiseta Mathcad tõlgendaks kahe vektori korrutamist skalaarkorrutisena). Seevastu paljud Mathcad'i funktsioonid ja operaatorid võtavad argumendina vastu ka vektori ja annavad tulemuseks samuti vektori, mis on saadud operatsiooni teostamisel element-kaupa. Sellisel juhul on vektoriseerimisoperaator ülearune ja kipub arvutamist aeglustama.
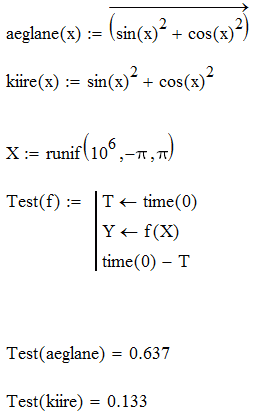
Töölehe mälukasutuse piiramine
Tavapärases arvutiteaduslikus tähenduses termin muutuja viitab kindlale nimega piirkonnale arvuti mälus. See mälupiirkond võetakse kasutusele muutuja deklareerimise või esmase omistamise hetkel ja programmi edasise täitmise käigus võib selle mälupiirkonna sisu korduvalt üle kirjutada erinevate väärtustega. Seevastu Mathcad'i töölehel defineeritud "muutuja" viitab pigem konstantsele väärtusele mälus, sest edasised definitsioonid selle mälupiirkonna sisu enam ei mõjuta. Kui samanimelisele muutujale edaspidi uus väärtus omistada, tähendab see lihtsalt uue konstantset väärtust säilitava mälupiirkonna kasutuselevõttu. Tänu sellele saab Mathcad'i tööleht sisaldada samaaegselt mitut samanimelist, aga erineva väärtusega muutujat. Teiselt poolt tähendab see aga seda, et kõik otse töölehel defineeritud muutujad (konstandid) jäävad arvuti mällu seni kuni vastav piirkond kustutatakse või kuni tööleht suletakse. Probleemseks võib olukord muutuda siis kui opereeritakse suurte arvumassiividega. Järgnevas näites tekib arvuti mällu mitte üks, vaid kolm suurt arvumassiivi:

Eeldusel et vahetulemused huvi ei paku, saab need ajutiselt talletada alamprogrammis lokaalsetes muutujates. Mathcad'i lokaalsed muutujad käituvad tõepoolest muutujatena ja neile reserveeritud mälu vabastatakse alamprogrammist väljumisel. Seega äsjase näite saab ökonoomsemalt kirja panna nii:
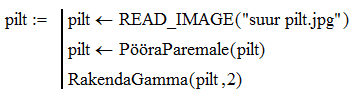
Täiendavad infoallikad
SisukordInternetis on saadaval rida eestikeelseid materjale , mis kordavad või täiendavad eelöeldut. Sirvida tasub ka Mathcad'i ressursikeskuse töölehti, kus saab kohe katsetada "elavate" näidetega (Help menüüst Tutorials, QuickSheets). Põhjaliku ülevaate annab Mathcad'iga kaasa tulev "Mathcad User's Guide" (leitav Mathcad'i kataloogi alamkaustast "doc"). Konkreetsemate probleemidega tuleks pöörduda abiinfo poole (Help → Mathcad help). Mathcad'i abiinfosüsteem on üsna hästi indekseeritud ja sobilike märksõnadega leiab kergesti vahendid spetsiifiliste ülesannete lahendamiseks. Isegi kui vajaliku funktsiooni nimi on juba teada, tuleb aegajalt ikkagi dokumentatsiooni sirvida, et meelde tuletada, kuidas täpselt konkreetset funktsiooni tuleb kasutada. Kui miski muu ei aita, võib abi otsida Mathcad'i kasutajate foorumist.