Eksperimendid alalisvooluga¶
TÜ Füüsika Instituut
Selles juhendis kirjeldatakse lihtsate arvutijuhitavate alalisvoolumõõtmiste realiseerimist Jupyteri keskkonnas, kasutades programmeerimiskeelena Pythonit. Käsitletakse eksperimente, kus pinge ja vool muutuvad võrdlemisi aeglaselt (sekundite diapasoonis või aeglasemalt), nii et hetksignaali mõõtmiseks saab kasutada tavalist (arvutiühendusega) multimeetrit. Lisaks läheb tarvis ka arvutiga juhitavat toiteallikat, mille digitaalset volt- või ampermeetrit saab kasutada täiendava mõõteriistana.
Katsevahendid¶
Seda laadi lihtsamad seadmed ühenduvad arvutiga järjestikliidese kaudu (RS232 standard). Kaasaegsetel arvutitel reeglina füüsilist jadaväratit enam ei ole, kuid need saab tekitada vastava USB lisaseadmega (pildil näitena 4 pordiga seade). Paljud aparaadid kasutavad virtuaalset jadaväratit, nii et need seadmed ühenduvad arvutiga otse USB kaabliga. Füüsiline RS232 liides ei vaja mingit lisatarkvara, USB-RS232 üleminek vajab siiski draiverit. Jadaväratiga seadmete juhtimine on võrdlemisi lihtne ja seisneb sageli lihtsalt teksti kujul käskude/info saatmisel/vastuvõtmisel. Vastav käsustik/andmete formaat on üldiselt iga seadme jaoks spetsiifiline.
Järgnevates katsetes multimeetriks on UNI-T UT61E. See võtab 2 lugemit sekundis ja maksimaalne näit on 22000. Üle jadavärati edastatavate andmete formaat on kirjeldatud siin.
 |
 |
Toiteallikaks on KORAD KD3005P (0–30 V, 0–5 A). Selle käsustik on kirjeldatud siin ja siin. On ka teisi mudeleid identse või sarnase funktsionaalsuse ja käsustikuga (nt Velleman PS3005D).
Ettevalmistused¶
Pythonis saab mugavalt järjestikpordiga suhelda kasutades teeki pySerial. Sõltuvalt kasutatavast Pythoni distributsioonist saab selle installeerida kas paketihalduri pip või conda abil:
pip install pyserial
või
conda install -c conda-forge pyserial
Lisaks on vaja vahendeid graafikute tegemiseks (matplotlib), aja mõõtmist/viivitamist (time) ja mudeli sobitamist vähimruutude meetodil (scipy.optimize.curve_fit).
import numpy as np
from matplotlib.pyplot import *
from matplotlib import rcParams
from serial import *
import serial.tools.list_ports as list_ports
import time
from scipy.optimize import curve_fit
%matplotlib notebook
Graafikute üldise kujunduse seadistamine:
rcParams['figure.figsize'] = 4, 3
rcParams['figure.dpi'] = 120
rcParams['lines.markersize'] = 6
rcParams['lines.markeredgewidth'] = 1
rcParams['axes.titlesize'] = 'medium'
rcParams['savefig.dpi'] = 200
Kuvame loetelu jadaväratitest. Tulemus võiks sarnaneda sellega, mida näitab ka Windowsi kontrollpaneel (Control Panel/Hardware and Sound/Device Manager/Ports).
for p in list(list_ports.comports()):
print(p)
Olles identifitseerinud pordid, mille külge aparaadid on ühendatud, jätame need edaspidiseks meelde:
COM_MM = 'COM1' # multimeeter
COM_PS = 'COM2' # toiteallikas
Seadmete programmeerimine¶
Mõistlik on iga konkreetse seadme juhtimine kapseldada omaette klassi. Kuna mingil määral on erinevatel seadmetel siiski ühine funktsionaalsus, tasub kasutada ka polümorfismi, st ühine funktsionaalsus realiseerida baasklassis ja sellest tuletada erinevad klassid vastavate konkreetsete seadmete jaoks.
Pythonis klassid defineeritakse võtmesõnaga class. Klassi mistahes meetodi defineerimisel esimeseks argumendiks on muutuja, mis viitab antud objektile (klassi eksemplarile), tavaliselt nimega self. Objekti liikmetele (nt muutujale serial) pääseb siis ligi kujul self.serial. Klassi koosseisus on ka spetsiaalseid meetodeid, mille nimi algab ja lõpeb kahe allkriipsuga. Näiteks klassi konstruktor on nimega __init__.
Esmalt loome baasklassi mistahes jadaväratiga seadmega suhtlemiseks:
class SerialDevice:
def __init__(self, port):
self.init()
self.serial.port = port
def open(self):
if not self.serial.is_open:
self.serial.open()
def close(self):
if self.serial.is_open:
self.serial.close()
def __enter__(self):
self.open()
return self
def __exit__(self, type, value, traceback):
self.close()
Selle koosseisus on meetodid open ja close, nii et seadme kasutamise sessioon näeb välja nii:
seade = Seade('COM1'):
seade.open()
# eksperiment
seade.close()
Siin Seade tähistab klassi, mis on tuletatud baasklassist SerialDevice, ning 'COM1' on konstruktori parameeter.
Seevastu meetodid __enter__ ja __exit__ lubavad teha sedasama mõnevõrra mugavamal kujul
with Seade('COM1') as seade:
# eksperiment
kus meetod open käivitatakse automaatselt with-bloki alguses ja meetod close lõpus. Seejuures viimane käivitatakse ka juhul kui with-blokis peaks tekkima programmiviga.
Siin ja edaspidi konstruktori ainsaks argumendiks on jadavärati nimi. Jadavärati seadistamine (andmevahetuskiirus, bittide arvud, jne) peab aset leidma meetodis init(), kus luuakse ka vastav Serial objekt. Selliseid seadistusi teab vaid tuletatud klass, mis on konkreetse aparaadiga seotud, seega meetod init() on baasklassis defineerimata.
Multimeeter¶
Järgmine klass loeb multimeetri UNI-T UT61E näidu. Multimeeter saadab andmeid pidevalt, umbes kaks lugemit sekundis. Andmepakett on 14 baiti, millest kaks baiti on realõpusümbolid (\n ja \r, ASCII koodid vastavalt 10 ja 13). Meetod lugem kontrollib, kas sisendpuhvris on uusi andmeid, interpreteerib jooksvalt iga tuvastatud 12 baidi pikkuse andmepaketi ja tagastab viimase lugemi.
class UT61E(SerialDevice):
ANDMED = {
48: { 48: -3 }, # 10 A
59: {48: -4, 49: -3, 50: -2, 51: -1, 52: -5}, # voldid
61: {48: -8, 49: -7}, # auto uA
63: {48: -6, 49: -5} # auto mA
}
def init(self):
self.serial = Serial(
baudrate = 19230, bytesize = SEVENBITS, parity = PARITY_ODD,
stopbits = STOPBITS_ONE
)
self.serial.rts = False
self.baidid = []
self.ootab_reavahetust = True
def lugem(self):
lugem = None
for b in self.serial.read_all():
if b == 10 or b == 13:
if self.ootab_reavahetust:
self.ootab_reavahetust = False
elif len(self.baidid) > 0:
lugem = self.teisenda()
elif not self.ootab_reavahetust:
self.baidid.append(b)
return lugem
def teisenda(self):
baidid = bytearray(self.baidid)
self.baidid.clear()
if len(baidid) != 12:
raise IOError("UT61E: loeti vale arv baite '%s'" % baidid.decode())
olek = baidid[7]
negat = olek & 0x4 == 0x4 # negatiivne väärtus?
if olek & 0x1 == 0x1: # ületäitumine?
return float('-inf') if negat else float('inf')
lugem = int(baidid[1:6])
if negat:
lugem = -lugem;
režiim = baidid[6]
piirkond = baidid[0]
if režiim not in UT61E.ANDMED:
raise IOError("UT61E: tundmatu režiim '%d'" % režiim)
piirkonnad = UT61E.ANDMED[režiim]
if piirkond not in piirkonnad:
raise IOError("UT61E: tundmatu tööpiirkond '%d'" % piirkond)
aste = piirkonnad[piirkond]
return lugem * 10**aste
Minimalistlik kood multimeetri testimiseks, nt lugemi võtmine iga sekundi tagant, kokku kolm mõõtmist:
with UT61E(COM_MM) as mm:
for i in range(3):
time.sleep(1)
print('%.4f' % mm.lugem())
Kuna antud multimeeter väljastab 2 lugemit sekundis, siis pooled neist lähevad antud näites kaotsi. Kõigi mõõtepunktide registreerimiseks tuleks tsükli aeg teha lühemaks kui 0,5 s, aga siis tuleb ka kontrollida, kas mm.lugem() tagastab arvulise väärtuse või None.
with UT61E(COM_MM) as mm:
lugemite_arv = 0
while lugemite_arv < 3:
lugem = mm.lugem()
if lugem is not None:
print('%.4f' % lugem)
lugemite_arv += 1
Toiteplokk¶
Kuna sarnaseid, vaid üksikutes detailides erinevaid toiteplokke on mitmeid, teeme esmalt baasklassi, mis kätkeb ühist funktsionaalsust. Meetodeid pinge ja vool saab välja kutsuda ühe argumendiga või ilma. Esimesel juhul seatakse vastav toiteploki režiim. Näiteks pinge(4.5) seab maksimaalse pinge 4,5 volti. Seejuures tuleks anda seadmele ka 2–3 sekundit aega uue seisundi stabiliseerimiseks.
Kui meetodid pinge ja vool kutsuda välja ilma argumentideta, siis tagastatakse vastavalt volt- või ampermeetri näit. Klassi Serial parameeter timeout = 1 annab mõista, et seadmele antakse reageerimiseks aega kuni 1 sekund.
class PSU(SerialDevice):
def init(self):
self.serial = Serial(
baudrate = 9600, bytesize = EIGHTBITS, parity = PARITY_NONE,
stopbits = STOPBITS_ONE, timeout = 1
)
def pinge(self, pinge=None):
if pinge is None:
self.serial.reset_input_buffer()
self.serial.write('VOUT1?'.encode())
baidid = self.serial.read(size=5)
if len(baidid) < 5:
raise IOError("UT61E: loeti vähem kui 5 baiti '%s'" % baidid.decode())
return float(baidid)
self.serial.write(('VSET1:%05.2f' % pinge).encode())
def vool(self, vool=None):
if vool is None:
self.serial.reset_input_buffer()
self.serial.write('IOUT1?'.encode())
baidid = self.serial.read(size=5)
if len(baidid) < 5:
raise IOError("UT61E: loeti vähem kui 5 baiti '%s'" % baidid.decode())
return float(baidid)
self.serial.write(('ISET1:%05.3f' % vool).encode())
Toiteplokil KD3005P on väljund püsivalt aktiivne, aga PS3005D võimaldab seda sisse/välja lülitada:
class PS3005D(PSU):
def toide_peale(self):
self.serial.write('OUT1'.encode())
def toide_maha(self):
self.serial.write('OUT0'.encode())
class KD3005P(PSU):
def toide_peale(self):
pass # ei tee midagi, funktsioon puudub
def toide_maha(self):
pass # ei tee midagi, funktsioon puudub
Edaspidi kasutame seadet KD3005P ja seega arvutijuhitavat toite lülitamise võimalust ei ole.
Kontrolliks seame pinge ja voolu piirid ning loeme näidikute väärtused:
with KD3005P(COM_PS) as ps:
ps.pinge(2)
time.sleep(1)
ps.vool(0.2)
time.sleep(1)
print('%.2f' % ps.pinge())
print('%.3f' % ps.vool())
Kuna ahel oli avatud, siis pinge saavutas seatud maksimumväärtuse ja voolutugevus jäi nulliks.
Toiteploki näidikute täpsus¶
Kontrollimaks toiteploki pingenäidiku täpsust, mõõdame pinget toiteploki klemmidel multimeetriga ja võrdleme saadud näite.
U_set = np.arange(0.5, 28, 0.5)
with UT61E(COM_MM) as mm:
with KD3005P(COM_PS) as ps:
U_ps = []
U_mm = []
for U in U_set:
ps.pinge(U)
time.sleep(3)
U_mm.append(mm.lugem())
U_ps.append(ps.pinge())
print('U_set = %4.1f, U_ps = %5.2f, U_mm = %7.4f' % (U, U_ps[-1], U_mm[-1]))
ps.pinge(1)
U_ps = np.array(U_ps)
U_mm = np.array(U_mm)
ΔU = np.sqrt(np.mean(np.square(U_ps - U_mm)))
print('ruutkeskmine erinevus = %.3f V' % ΔU)
Analoogiliselt võrdleme ampermeetrite näite:
I_set = np.arange(0.01, 0.22, 0.01)
with UT61E(COM_MM) as mm:
with KD3005P(COM_PS) as ps:
I_ps = []
I_mm = []
for I in I_set:
ps.vool(I)
time.sleep(3)
I_mm.append(mm.lugem())
I_ps.append(ps.vool())
print('I_set = %.2f, I_ps = %.3f, I_mm = %.5f' % (I, I_ps[-1], I_mm[-1]))
ps.vool(0.01)
I_ps = np.array(I_ps)
I_mm = np.array(I_mm)
ΔI = np.sqrt(np.mean(np.square(I_ps - I_mm)))
print('ruutkeskmine erinevus = %.4f A' % ΔI)
Milliamprite piirkonnas mõõtes jääb täpsusest 3 mA siiski väheks, seetõttu järgnevas kasutame sekundaarse mõõteriistana vaid toiteploki voltmeetrit. Sel juhul voolutugevuse mõõtmiseks tuleb lihtsalt ahelasse lisada järjestikku paraja suurusega takisti ja mõõta multimeetriga sellel tekkivat pingelangu.
Hõõglambi voltamperkarakteristik¶
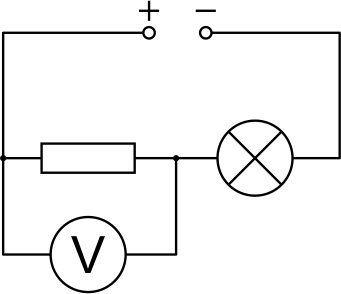Koostame joonisel kujutatud elektriskeemi. Hõõglamp on ühendatud järjestikku paraja suurusega takistiga. Multimeetriga mõõdetakse takistil tekkivat pingelangu ja selle järgi voolutugevust ahelas. Toiteploki väljundpinge ja takisti pingelangu vahe kaudu saame teada ka pinge lambil.
Alternatiivselt võiks multimeetriga mõõta pinget lambil. Optimaalne variant sõltub komponentide valikust. Ideaalis võiks mõlemad mõõteriistad töötada üle kogu oma mõõtepiirkonna, ning voltmeetrite näidud peaksid olema oluliselt erinevad, et kahe pingenäidu lahutamisel ei tekiks suurt suhtelist viga.
U_set = np.arange(0.5, 15.1, 0.5)
U_ps = []
U_mm = []
with UT61E(COM_MM) as mm:
with KD3005P(COM_PS) as ps:
for U in U_set:
ps.pinge(U)
time.sleep(3)
U_mm.append(mm.lugem())
U_ps.append(ps.pinge())
print('U_ps = %5.2f, U_mm = %.4f' % (U_ps[-1], U_mm[-1]))
ps.pinge(1)
U_ps = np.array(U_ps)
U_mm = np.array(U_mm)
Teostame esmased arvutused ja graafikud. Alati salvestame vähemalt otsesed mõõtmistulemused, et neid saaks edaspidi failist laadida ja analüüsida ilma katset kordamata.
fail = 'lambi_voltamper'
takistus = 20.5
U_lamp = U_ps - U_mm
I_lamp = U_mm / takistus
np.savetxt(fail + '.txt', np.column_stack((U_ps, U_mm, U_lamp, I_lamp)), fmt='%.8f')
plot(U_lamp, I_lamp, 'r.')
xlabel('Pinge (V)')
ylabel('Vool (A)')
grid()
savefig(fail + '.png', bbox_inches='tight')
show()
Edasiseks analüüsiks võime kasutada äsja mõõdetud andmeid (kui need on veel arvuti mälus) või vajadusel taastame need failist:
U_ps, U_mm, U_lamp, I_lamp = np.loadtxt('lambi_voltamper.txt').T
Lihtsaim hõõglambi mudel ennustab pinge ja voolu vahel astmeseost: $I=aU^b$.
mudel = lambda U, a, b: a*U**b
a, b = 0.1, 0.5
(a, b), _ = curve_fit(mudel, U_lamp, I_lamp, (a, b))
print('a = %.3f, b = %.3f' % (a, b))
U = np.linspace(0, 13, 100)
plot(U_lamp, I_lamp, 'r.')
plot(U, mudel(U, a, b), 'b-')
xlabel('Pinge (V)')
ylabel('Vool (A)')
grid()
savefig(fail + '_mudel.png', bbox_inches='tight')
show()
Dioodi voltamperkarakteristik¶
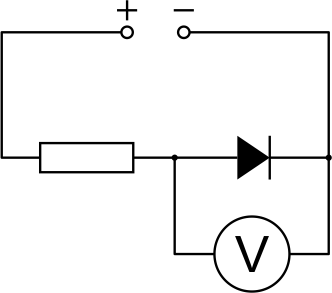Seekord on mõistlik multimeetriga mõõta pinget dioodil, kuna pärast dioodi avanemist dioodi pinge muutub võrdlemisi aeglaselt.
U_set = np.geomspace(0.25, 7.1, 25)
U_ps = []
U_mm = []
with UT61E(COM_MM) as mm:
with KD3005P(COM_PS) as ps:
for U in U_set:
ps.pinge(U)
time.sleep(3)
U_mm.append(mm.lugem())
U_ps.append(ps.pinge())
print('U_ps = %.2f, U_mm = %.4f' % (U_ps[-1], U_mm[-1]))
ps.pinge(1)
U_ps = np.array(U_ps)
U_mm = np.array(U_mm)
fail = 'dioodi_voltamper'
takistus = 20.5
U_diood = U_mm
I_diood = (U_ps - U_mm) / takistus
np.savetxt(fail + '.txt', np.column_stack((U_ps, U_diood, I_diood)), fmt='%.8f')
plot(U_diood, I_diood, 'r.')
xlabel('Pinge (V)')
ylabel('Vool (A)')
grid()
savefig(fail + '.png', bbox_inches='tight')
show()
Shockley dioodi mudel ennustab $$I=I_\text{s}\left[\exp\left(\frac{U}{nU_T}\right)-1\right],$$ kus $I_s$ on küllastav vool vastupingestatud dioodis, $U_T=k_\text{B}T/q$ (toatemperatuuril 25,4 mV) ja $n$ iseloomustab dioodi ideaalsust.
U_T = 0.025421
mudel = lambda U, I_s, n: I_s * (np.exp(U/(n * U_T)) - 1)
I_s, n = 1e-14, 1
(I_s, n), _ = curve_fit(mudel, U_diood, I_diood, (I_s, n))
print('I_s = %.3g A, n = %.2f' % (I_s, n))
U = np.linspace(0.2, 0.79, 100)
plot(U_diood, I_diood, 'r.')
plot(U, mudel(U, I_s, n), 'b-')
xlabel('Pinge (V)')
ylabel('Vool (A)')
grid()
savefig(fail + '_mudel.png', bbox_inches='tight')
show()
Aku tühjenemine¶
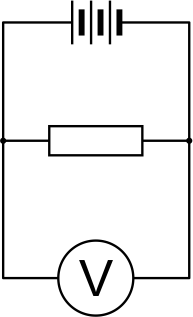Tühjendame täis laetud NiMH-aku üle mõistliku suurusega takisti, jälgides aku pinge muutumist multimeetriga. Teades takistust, saame ühtlasi teada voolutugevuse ja selle kaudu elektrilaengu. Seega selles katses on vaja vaid multimeetrit.
aeg = []
pinge = []
with UT61E(COM_MM) as mm:
time.sleep(2)
t0 = time.time()
while True:
aeg.append(time.time() - t0)
pinge.append(mm.lugem())
print('aeg = %6.1f s; pinge = %6.4f V' % (aeg[-1], pinge[-1]))
if (pinge[-1] < 0.5):
break
time.sleep(5)
aeg = np.array(aeg)
pinge = np.array(pinge)
Teades aega ja voolutugevust, saame ülekantud elektrilaengu leida integreerimise teel (näiteks trapetsmeetodiga).
fail = 'aku_tühjenemine'
takistus = 7.23
vool = pinge / takistus
np.savetxt(fail + '.txt', np.column_stack((aeg, pinge, vool)), fmt='%.8f')
print('Mahtuvus %.3g mAh' % (np.trapz(vool, aeg) * (1000 / 3600)))
plot(aeg, pinge, 'r-')
xlabel('Aeg (s)')
ylabel('Pinge (V)')
grid()
tight_layout()
savefig(fail + '.png', bbox_inches='tight')
show()
Kondensaator¶
Laadumine¶
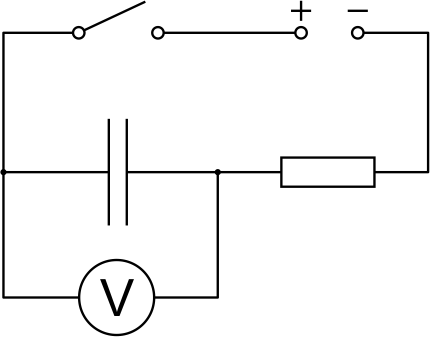Kondensaatori laadumise uurimiseks koostame joonisel kujutatud elektriskeemi. Eelnevalt veendume, et kondensaator on tühjaks laetud. Toiteplokile on seatud kindla suurusega pinge (ja seda ei ole tarvis arvutist juhtida). Käivitame mõõtmise ja mõne hetke pärast sulgeme lüliti.
Nendes katsetes kasutame superkondensaatorit nimimahtuvusega $C=$ 1,5 F, nii et isegi võrdlemisi väikese takistuse $R$ puhul on ajakonstant $RC$ minutite diapasoonis ja seega pinge muutused kergesti jälgitavad.
aeg = []
pinge = []
with UT61E(COM_MM) as mm:
t0 = time.time()
while True:
lugem = mm.lugem()
if lugem is not None:
aeg.append(time.time() - t0)
pinge.append(lugem)
print('aeg = %6.1f s; pinge = %6.3f V' % (aeg[-1], pinge[-1]))
if aeg[-1] > 4000:
break
time.sleep(0.1)
aeg = np.array(aeg)
pinge = np.array(pinge)
fail = 'kondensaatori_laadumine'
np.savetxt(fail + '.txt', np.column_stack((aeg, pinge)), fmt='%.8f')
plot(aeg, pinge, 'r-')
xlabel('Aeg (s)')
ylabel('Pinge (V)')
grid()
tight_layout()
savefig(fail + '.png', bbox_inches='tight')
show()
aeg, pinge = np.loadtxt('kondensaatori_laadumine.txt').T
Kui saadud graafikut suumida, on näha, et alguses mõned hetked (enne lüliti L2 sulgemist) on pinge null. Eemaldame need andmepunktid ja nihutame vastavalt ajatelge. Ühtlasi arvutame voolutugevuse.
toitepinge = 9.994
takistus = 506.7
laadub = aeg > 9.1
aeg = aeg[laadub]
aeg -= aeg[0]
pinge = pinge[laadub]
vool = (toitepinge - pinge) / takistus
Kui kondensaatorit mahtuvusega $C$ laaditakse konstantse pingega $U_0$ üle takisti $R$, siis kondensaatori pinge kasvab ajas järgmiselt: $$U(t)=U_0\left[1-\exp\left(-\frac{t}{CR}\right)\right].$$ Teiste sõnadega, voolutugevus kahaneb eksponentsiaalselt: $$I(t)=\frac{U_0-U(t)}{R}=I_0\exp\left(-\frac{t}{CR}\right).$$ See mudel põhineb eeldusel, et kondensaatori laeng on võrdeline pingega, $Q=CU$ (st mahtuvus $C$ on konstantne), ja kondensaatoril endal mingit täiendavat relaksatsiooniaega ei ole. Selgub, et superkondensaatori (ja ka mõnede elektrolüütkondensaatorite) korral need eeldused ei pea paika, sest ioonide difundeerumine ja laengu relakseerumine poorsetel elektroodidel on võrdlemisi keerulised ja aeglased protsessid.
Seega voolutugevuse käik logaritmilisel graafikul ei tule päris sirge:
plot(aeg, vool, 'r-')
yscale('log')
xlabel('Aeg (s)')
ylabel('Vool (A)')
grid()
tight_layout()
savefig(fail + '_vool.png', bbox_inches='tight')
show()
Kui saadud sõltuvuse algusosa lähendada sirgele, saame vastavas lähenduses siiski mahtuvust hinnata:
n = len(aeg) // 5 # esimene viiendik andmepunktidest
# lähendame parabooliga, aga kasutame vaid selle algtõusu
_, tõus, algordinaat = np.polyfit(aeg[:n], np.log(vool[:n]), 2)
mahtuvus = -1 / (takistus * tõus)
print('Mahtuvus %.3f F' % mahtuvus)
t = np.linspace(0, 2100, 100)
plot(aeg, vool, 'r-', label='katse')
plot(t, np.exp(tõus * t + algordinaat), 'b--', label='lineaarne mudel')
yscale('log')
xlabel('Aeg (s)')
ylabel('Vool (A)')
axvline(aeg[n], color='red', lw=0.5)
grid()
legend()
tight_layout()
savefig(fail + '_mudel.png', bbox_inches='tight')
show()
Tühjenemine¶
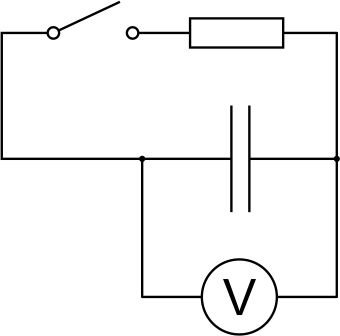Seame toiteallikale mõistliku suurusega pinge ja voolu, ja laadime sellega kondensaatori. Seejärel asetame kondensaatori näidatud elektriskeemi, käivitame mõõtmise ning mõne hetke pärast sulgeme lüliti.
aeg = []
pinge = []
with UT61E(COM_MM) as mm:
t0 = time.time()
while True:
lugem = mm.lugem()
if lugem is not None:
aeg.append(time.time() - t0)
pinge.append(lugem)
print('aeg = %6.1f s; pinge = %6.3f V' % (aeg[-1], pinge[-1]))
if aeg[-1] > 6000:
break
time.sleep(0.1)
aeg = np.array(aeg)
pinge = np.array(pinge)
fail = 'kondensaatori_tühjenemine'
np.savetxt(fail + '.txt', np.column_stack((aeg, pinge)), fmt='%.8f')
plot(aeg, pinge, 'r-')
xlabel('Aeg (s)')
ylabel('Pinge (V)')
grid()
tight_layout()
savefig(fail + '.png', bbox_inches='tight')
show()
tühjeneb = aeg > 13.7
aeg = aeg[tühjeneb]
aeg -= aeg[0]
pinge = pinge[tühjeneb]
vool = pinge / takistus
n = len(aeg) // 4
_, tõus, algordinaat = np.polyfit(aeg[:n], np.log(pinge[:n]), 2)
mahtuvus = -1 / (takistus * tõus)
print('Algmahtuvus %.3f F' % mahtuvus)
t = np.linspace(0, 3500, 100)
plot(aeg, pinge, 'r-', label='katse')
plot(t, np.exp(tõus * t + algordinaat), 'b--', label='lineaarne mudel')
yscale('log')
xlabel('Aeg (s)')
ylabel('Pinge (V)')
axvline(aeg[n], color='red', lw=0.5)
grid()
legend()
tight_layout()
savefig(fail + '_mudel.png', bbox_inches='tight')
show()
Laengu sõltuvus pingest¶
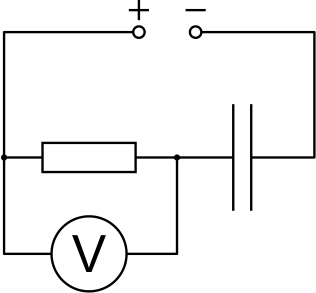Et täpsemalt karakteriseerida sellise kondensaatori omadusi, püüame mõõta kondensaatorisse kogunenud laengu sõltuvuse rakendatud pingest. Selleks laadime kondensaatorit läbi takisti, ja takistil tekkiva pingelangu järgi saame jälgida voolutugevuse muutumist. Voolutugevuse integreerimise teel saame hiljem arvutada ülekantud laengu. Toiteploki pinget tõstame 2 V sammuga. Pärast toitepinge tõstmist ootame, kuni voolutugevus muutub piisavalt väikeseks. Seejuures me muidugi eeldame, et kondensaatori isetühjenemine (lekkevoolu tõttu) toimub oluliselt pikemates ajamastaapides ja seda võib ignoreerida.
U_set = np.arange(2, 10.1, 2.0)
takistus = 20.5
andmed = []
with UT61E(COM_MM) as mm:
with KD3005P(COM_PS) as ps:
for U in U_set:
print('======= toitepinge = %5.2f V =======' % U)
time.sleep(1)
ajutine = []
t0 = time.time()
ps.pinge(U)
while True:
pinge = mm.lugem()
aeg = time.time() - t0
if pinge is not None:
print('aeg = %5.1f s, pinge = %6.4f V' % (aeg, pinge))
ajutine.append((aeg, pinge, pinge / takistus))
if aeg > 1500 or (aeg > 100 and pinge < 0.002):
break
time.sleep(0.1)
andmed.append(np.array(ajutine))
Järjendis andmed on nüüd hulk erineva suurusega massiive, ja lisaks tuleks salvestada ka U_set. Ühte tekstifaili (numpy.savetxt abil) selliseid erineva suurusega massiive ei saa paigutada. Kuid numpy.save abil saab tervikuna binaarfaili salvestada mistahes massiivi sarnase objekti, mille elemendid võivad samuti olla massiivid.
fail = 'kondensaatori_pinge_laeng'
np.save(fail, [U_set] + andmed, allow_pickle=True) # faili laiend .npy lisatakse automaatselt
for U, seeria in zip(U_set, andmed):
plot(seeria[:,0], 1000 * seeria[:,2], label='%.1f V' % U)
xlabel('Aeg (s)')
ylabel('Vool (mA)')
yscale('log')
legend()
tight_layout()
savefig(fail + '.png', bbox_inches='tight')
show()
Andmete taastamine failist on analoogne:
andmed = np.load('kondensaatori_pinge_laeng.npy', allow_pickle=True)
U_set = andmed[0]
andmed = andmed[1:]
Kondensaatorisse kogunenud elektrilaengu saame jällegi integreerimise teel:
laeng = np.cumsum( [np.trapz(seeria[:,2], seeria[:,0]) for seeria in andmed] )
plot(U_set, laeng, 'r.-')
xlim(left=0)
ylim(bottom=0)
xlabel('Pinge (V)')
ylabel('Laeng (C)')
grid()
tight_layout()
show()
Ootuspäraselt saadud sõltuvus ei ole päris lineaarne. Pigem tuleks lineaarsele liikmele lisada ka ruutliige: $Q=aU+bU^2$, kus $a$ annab mahtuvuse väikeste pingete juures.
mudel = lambda U, a, b: a*U + b*U*U
a, b = 1, 0.02
(a, b), _ = curve_fit(mudel, U_set, laeng, (a, b))
print('Mahtuvus väikestel pingetel = %.3f F' % a)
U = np.linspace(0, 10, 100)
plot(U_set, laeng, 'r.')
plot(U, mudel(U, a, b), 'b-')
plot(U, a*U, 'b--')
xlim(left=0)
ylim(bottom=0)
xlabel('Pinge (V)')
ylabel('Laeng (C)')
grid()
tight_layout()
savefig(fail + '_mudel.png', bbox_inches='tight')
show()
Kuna $Q$ ja $U$ seos ei ole enam lineaarne, tuleb eristada integraalset mahtuvust $$\frac{Q}{U}=a+bU$$ ja diferentsiaalset mahtuvust $$\frac{dQ}{dU}=a+2bU.$$
plot(U, a + b * U, 'r-', label='integ. mahtuvus')
plot(U, a + 2 * b * U, 'b-', label='difer. mahtuvus')
xlabel('Pinge (V)')
ylabel('Mahtuvus (F)')
grid()
legend()
tight_layout()
savefig(fail + '_mahtuvus.png', bbox_inches='tight')
show()
Mäluefekt¶
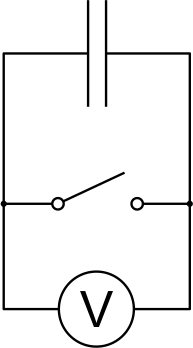Super- või elektrolüütkondensaatoreid ei ole võimalik lühikese ajaga täiesti tühjaks laadida. Selles veendumiseks teeme järgmise katse. Laeme kondensaatori eelnevalt teatud pingeni ja ootame mõninga aja kuni kondensaatori seisund on stabiliseerunud. Seejärel lülitame külge multimeetri, nagu näidatud joonisel, ja käivitame mõõtmise. Mõne aja pärast lühistame kondensaatori paariks sekundiks, kuni pinge kondensaatoril kukub nulli. Pärast lühise kõrvaldamist hakkab pinge taastuma.
aeg = []
pinge = []
with UT61E(COM_MM) as mm:
t0 = time.time()
while True:
lugem = mm.lugem()
if lugem is not None:
aeg.append(time.time() - t0)
pinge.append(lugem)
print('aeg = %6.1f s; pinge = %6.4f V' % (aeg[-1], pinge[-1]))
if aeg[-1] > 6000:
break
time.sleep(0.1)
aeg = np.array(aeg)
pinge = np.array(pinge)
fail = 'kondensaatori_tühjenemine_mälu'
np.savetxt(fail + '.txt', np.column_stack((aeg, pinge)), fmt='%.8f')
plot(aeg, pinge, 'r-')
xlabel('Aeg (s)')
ylabel('Pinge (V)')
grid()
tight_layout()
savefig(fail + '.png', bbox_inches='tight')
show()
Põhjalikuma katsetamisega võiks ka veenduda, et taastumisel pinge saavutab seda suurema väärtuse, mida kõrgema pingeni oli kondensaator algselt laetud.
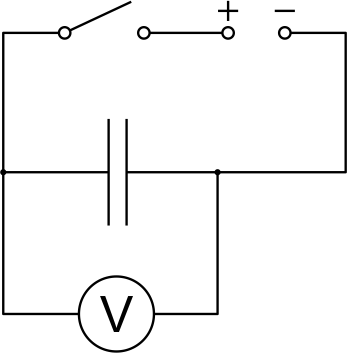Sama efekti võib näha ka kondensaatori äkilisel laadimisel. Ühendame algselt tühjaks laetud kondensaatori elektriskeemi, mis on näidatud joonisel. Seame toiteplokil pinge 2 V ja voolutugevuse 0,4 A ja käivitame mõõtmise. Mõne hetke pärast sulgeme lüliti. Pinge kondensaatoril hakkab kiiresti kasvama (tempoga $I/C$) kuni saavutab maksimumi 2 V, seejärel voolutugevus hakkab kahanema. Sel hetkel avame lüliti.
aeg = []
pinge = []
with UT61E(COM_MM) as mm:
t0 = time.time()
while True:
lugem = mm.lugem()
if lugem is not None:
aeg.append(time.time() - t0)
pinge.append(lugem)
print('aeg = %6.1f s; pinge = %6.4f V' % (aeg[-1], pinge[-1]))
if aeg[-1] > 6000:
break
time.sleep(0.1)
aeg = np.array(aeg)
pinge = np.array(pinge)
fail = 'kondensaatori_laadumine_mälu'
np.savetxt(fail + '.txt', np.column_stack((aeg, pinge)), fmt='%.8f')
plot(aeg, pinge, 'r-')
xlabel('Aeg (s)')
ylabel('Pinge (V)')
grid()
tight_layout()
savefig(fail + '.png', bbox_inches='tight')
show()
