Compensating for Transparency

In scientific plots, one often needs the regions that show various areas to be semi-transparent in order for their overlap to be visible. A common problem is that with transparency, a chosen colour will be lighter and look different than originally intended. This can be compensated for by making the colour darker, so it will look the same. Taking a completely opaque background in the transparency formula, the compensated colour $c_s$ is given by

\begin{equation} c_s = 1 + \frac{c_r - 1}{a_s}, \end{equation} where $c_r$ is the chosen colour and $a_s$ the chosen background value. To RGB colours, for example, this formula must be applied to all components.

To avoid an unphysical value $c_s < 0$ (negative component values are commonly clipped to zero for RGB or CMYK colours), one must have $c_r > 1 - a_s$. But also note that $c_r = 1$ yields an unchanged $c_s = 1$, so one must also have $c_r < 1$ for all components to avoid producing an off-tint colour.

The image below shows two opaque squares of different colours on the left, two squares of the same colours with transparency added in the centre, and at right with darker colours to compensate for transparency ($a_s = 0.5$).

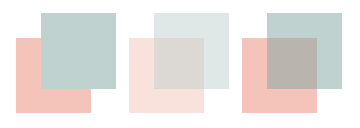
• Mathematica code and examples
• Asymptote code

In the code, the colour is converted to RGB, applied transparency compensation, and converted back to its original colour space.