Läbipaistvuse kompenseerimine

Teadusgraafikas on tihti tarvis pool-läbipaistvaid piirkond, et oleks näha nende kattuvus. Kuid iga värvitoon on läbipaistvana heledam ja näeb teistmoodi välja. Abi saab sellest, kui teha värv tumedamaks, et see pool-läbipaistvana näeks välja samasugune kui alguses. Võttes läbipaistvuse valemis täiesti läbipaistmatu tausta, on tumedam värv $c_s$ antud valemiga

\begin{equation} c_s = 1 + \frac{c_r - 1}{a_s}, \end{equation} kus $c_r$ i on algne värv ja $a_s$ on läbilaskvuse (opacity) väärtus. Seda valemit tuleb näiteks RGB värviruumis rakendada eraldi igale värvi komponendile.

Et vältida ebafüüsikalist väärtust $c_s < 0$ (RGB ja CMYK värvidel pannakse negatiivsed väärtused tavaliselt nulliks), peab kehtima $c_r > 1 - a_s$. Pange ka tähele, et $c_r = 1$ annab samuti $c_s = 1$, seega peab olema $c_r < 1$ iga RGB komponendi jaoks, et vältida värvitooni muutumist.

Pildil on vasakul kaks läbipaistmatut eri värvi ruutu, keskmistel ruutudel on lisatud läbipaistvus $a_s = 0.5$, paremal aga on värvid tehtud tumedamaks, et läbipaistvust kompenseerida.

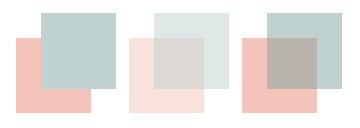
• Mathematica kood ja näited
• Asymptote'i kood

Koodis konverteeritakse värv RGB-ks, tehakse tumedamaks ja konverteeritakse tagasi algsesse värviruumi.