Loodusteaduse ülesannete vastuseid
Füüsika & keemia
Raskuskiirendus
- Ülesanne ja vastus [PDF, 52 KiB, 2 lk.]
Raskusjõud kahe keha vahel on
$F = {G m_1 m_2}/r^2$,
kus $G$ on gravitatsioonikonstant, $m_1$ ja $m_2$ kehade massid ning $r$ nendevaheline kaugus.
Meid huvitab aga väikesele kehale massiga $m$ mõjuv raskuskiirendus $g$ planeedi lähedal, mille mass on $M$ ja raadius $R$.
Newtoni teise seaduse järgi $F = m a$.
Gravitatsioonijõud planeedi ja tema pinnal oleva keha vahel on ühelt poolt
$F = {G M m}/R^2$,
teisalt defineeritud kui
$F = m g$.
Leiame, et
$g = {G M}/R^2$.
Kui $g$ on planeedi suurusest sõltumata konstant, siis peab olema
$M/R^2 = g/G = const$,
s.t. planeedi mass on võrdeline tema raadiuse ruuduga!
Tulemus on veider: $M$ võiks olla pigem võrdeline $R^3$, kuid isegi see eeldab, et planeedi tihedus on igal pool sama.
Kui mass on võrdeline raadiuse ruuduga, s.t. pindalaga, peaks see tähendama, et kogu planeedi mass on tema pinna lähedal — ulmefilmiplaneedid on seest tühjad!
Kui suur peab siis olema sfäärilise kesta tihedus? Maa raadius on umbes $R_⊕ = 6400 \text{km}$ ja mass $M_⊕ = 6 \times 10^24 \text{kg}$. Maa pindala on $S_⊕ = 4 π R_⊕^2 = 5 \times 10^8 \text{km}^2$. Ühe ruutkilomeetri kohta tulev mass on $10^16 \text{kg}$, ühe ruutmeetri kohta $10^10 \text{kg}$.
Kui Maa-suuruse planeedi kesta paksus oleks $1 \text{km}$, on tema tihedus $10^7 \text{kg/m}^3$. Maa keskmine tihedus on umbes $5500 \text{kg/m}^3$, ligi kümme tuhat korda väiksem; valge kääbuse täheaine tihedus on vaid 100 korda suurem!
Kui kest ka tekiks, kukuks ta omaenese raskuse all kokku.
On märksa realistlikum viis planeedi pinnal samasugust raskuskiirendust hoida: tuleb muuta tavalise seest täis planeedi raske raud-nikkeltuuma ja suhteliselt väikese tihedusega kesta vahekorda.
Eeldame, et planeedil raadiusega $R$ on tuum raadiusega $R_\text{c}$ (mõistagi $R_\text{c} < R$). Tuuma tihedus olgu $\rho_\text{s}$ ja planeedi koore tihedus $\rho_\text{c}$ (mõistagi $\rho_\text{s} < \rho_\text{c}$).
Siis on planeedi mass $M$ tuuma ja koore masside summa:
$M = V_\text{c} \rho_\text{c} + V_\text{s} \rho_\text{s} = 4/3 π R_\text{c}^3 \rho_\text{c} + (4/3 π R^3 - 4/3 π R_\text{c}^3) \rho_\text{s} = 4/3 π R^3 [\rho_\text{s} + \chi^3 (\rho_\text{c} - \rho_\text{s})]$,
kus defineerime raadiuste suhte $\chi = R_\text{c}/R$.
Me teame, et ulmefilmiplaneedi jaoks on
$M/R^2 = g/G$.
Seega
$g/G = 4/3 π R [\rho_\text{s} + \chi^3 (\rho_\text{c} - \rho_\text{s})]$,
kust tuuma ja planeedi (kesta) raadiuste suhe on
$\chi(R) = \left(\frac{-3 g/G + 4 \pi R \rho_\text{s}}{4 \pi R ( \rho_\text{s}-\rho_\text{c})}\right)^{\frac{1}{3}}$.
Teeme graafiku, kui $\rho_\text{s} = 4000 \text{kg/m}^3$ ja $\rho_\text{c} = 20000 \text{kg/m}^3$.
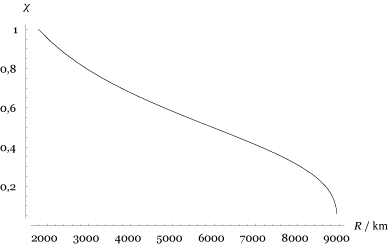
Tuuma ja planeedi raadiuste suhte $\chi$ sõltuvus planeedi raadiusest $R$, kui raskuskiirendus planeedi pinnal on $g$.
Jooniselt näeme, et selle triki abil saame teha planeete nõnda väikese raadiusega kui $1800 \text{km}$ või nõnda suurega kui $8800 \text{km}$. (Kuna tegu on jämeda hinnanguga, on tegelik vahemik väiksem