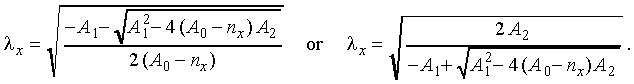
Figure 1
In the manuals of the practical works [Optika praktikum VII. Koostanud A.Haav. Tartu, TÜ, 1990, lk.58-67 or Praktikum po optike VII. Sostavitel` A.Haav. Tartu, TU, 1991, s.63-73] the calibration of the monochromator is based on the construction of the monochromator drum reading versus wavelength plot on a diagram paper with the following determination of the unknown wavelength of spectral lines from this plot. The calibration and the determination can be done more readily and with greater accuracy using a PC.
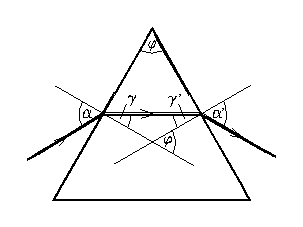
As we know, in the position of the minimum deviation the ray passes through the prism symmetrically (Figure 1):

Figure 1
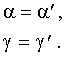
Consequently, in this position the angle of refraction ![]() is always
is always 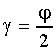 , where
, where ![]() is the prism refracting angle (the apex angle), and due to the
prism material dispersion
is the prism refracting angle (the apex angle), and due to the
prism material dispersion ![]() the angle of incidence
the angle of incidence ![]() must be different for different wavelengths
must be different for different wavelengths ![]() :
:
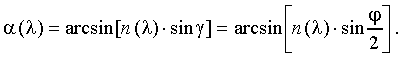
In the monochromator UM-2 the Abbe prism is used, that means that the refracting flint-glass prism is cut into halves along the apex angle bisector (prisms 1' and 1'') and these parts are glued together with a total reflection prism 2 in the way shown in Figure 2.
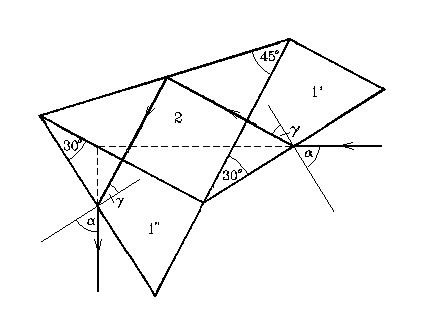
Such an arrangement ensures that in the minimum of deviation the incident and deviated rays are perpendicular to each other. Therefore to find the right angle of incidence at a given wavelength, the prism is rotated around his axis with the help of micrometer screw (a big cylindrical drum provided with the scale).
For the calibration one must determine the correspondence between the drum
scale reading N and the wavelength ![]() , but the respective relation is not linear. Linear is the
relation between the scale reading, which determines the prism position with
respect to incident beam, and the corresponding angle of incidence. Hence it
follows an idea for the monochromator calibration and the determination of the
wavelengths of unknown spectral lines by the computation.
, but the respective relation is not linear. Linear is the
relation between the scale reading, which determines the prism position with
respect to incident beam, and the corresponding angle of incidence. Hence it
follows an idea for the monochromator calibration and the determination of the
wavelengths of unknown spectral lines by the computation.
The refracting prism of the monochromator UM-2 is made of the heavy flint glass TF3 which standard dispersions are as follows [A.S.Toporets. Monokhromatory. M.,1955]
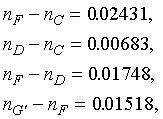
![]() and the Abbe number
and the Abbe number 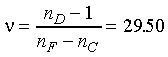 .
.
The standard indices of refraction of the glass TF3 can also be used [K.I.Tarasov. Spektral`nye pribory. L., 1977]:
Table
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The computation is made up of the following steps:
1) Having calculated the indices of refraction corresponding to the Fraunhofer lines C, D, F and G, or using the data from the table we can draw up a system of quadratic equations relying on the Cauchy formula:
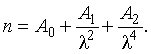
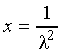 and
and 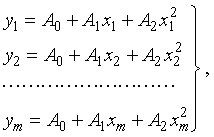
and resolving it by the method of least squares, we get the best fitting coefficients A0, A1, A2 of the Cauchy formula:
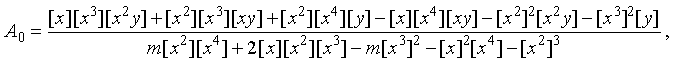
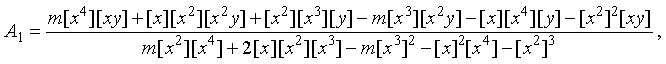
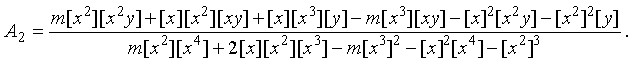
Here the Gauss brackets enable to shorten the writing of formulas: 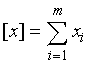 ,
, 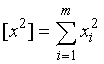 ,
, 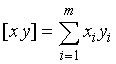 , etc.
, etc.
2) Knowing the coefficients of the Cauchy formula one can calculate at first
the refractive index ![]() of the prism material for the given wavelength
of the prism material for the given wavelength ![]() and then the corresponding angle of incidence
and then the corresponding angle of incidence ![]() at the minimum of deviation because the refracting angle of
prism is also known (
at the minimum of deviation because the refracting angle of
prism is also known (![]() ).
).
3) Using the mercury or the mercury-cadmium spectral lamp and recording the
scale readings, corresponding to all spectral lines, one can compute the
coefficients of regression formula relying on the easily recognizable Hg-lines:
690.7, 623.4, 579.1, 577.0, 491.6, 435.8, 404.7 and those of Cd-lines: 643.8,
508.6, 480.0, 467.8 nm. To obtain the regression coefficients we must at first
calculate the refractive indices ni
corresponding to the recognized Hg-lines ![]() , and then the angles of incidence
, and then the angles of incidence
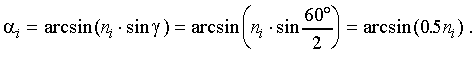
The regression coefficients a and b are calculated from the system of equations
where Ni is the drum scale reading, corresponding to the
wavelength![]() .
.
4) The determination of the unknown line wavelengths proceeds in the reverse order. For the scale reading Nx we find the corresponding angle of incidence
then the refractive index
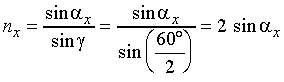 ,
,and finally the wavelength to be sought from the Cauchy formula