Answers to Problems in Natural Science
Physics & Chemistry
Acceleration Due to Gravity
- The problem and the answer [PDF, 56 KiB, 2 pp.]
The force of gravity between two spherical bodies is \begin{equation} F = {G m_1 m_2}/r^2 \end{equation}, where $G$ is the gravitational constant, $m_1$ and $m_2$ are masses of the bodies, and $r$ is the distance between them.
We are interested of the acceleration due to gravity $g$ of a planet, whose mass is $M$ and radius is $R$, on a small body with mass $m$.
Newton’s second law says that $F = m a$.
The force of gravity between the body on the surface of the planet is on one hand
$F = {G M m}/R^2,$
on the other hand defined as
$F = m g$.
We find that
$g = {G M}/R^2$.
If $g$ is constant independent of the mass of the planet, then we have
$M/R^2 = g/G = \text{const}$,
that is, the mass of the planet is proportional to its radius squared!
It is quite an odd result: $M$ rather ought to be proportional to $R^3$, but even that assumes that the planet is of uniform density.
If mass is proportional to the square of radius, i.e. to the surface area of the planet, it looks like the whole mass of the planet is near its surface: the planet is hollow!
How dense must the spherical shell be? The radius of the Earh is about $R_⊕ = 6400$ km and its mass $M_⊕ = 6 \times 10^{24}$ kg. Its surface area is then $S_⊕ = 4 \pi R_⊕^2 = 5 \times 10^8$ kg. The mass per one square kilometre is $10^{16}$ kg, per one square metre: $10^{10} \text{kg}$.
If the thickness of the shell of an Earth-sized planet were $1 \text{km}$, its density would be about $10^7 \text{kg/m}^3$. The average density of the Earth is about $5500 \text{kg/m}^3$, almost ten thousand times less; the density of white dwarf star matter is only 100 times larger!
(What would happen to the shell, even if it could be formed?)
There is a much more realistic way to hold the acceleration due to gravity constant: one has to change the ratio of radii of the high density iron-nickel core and and the relatively less dense shell of a quite ordinary planet.
Let’s assume that the planet with radius $R$ has a core with radius $R_c$ (of course, $R_c < R$). Let the density of the core be $\rho_\text{c}$ and the density of the shell $\rho_\text{s}$ (of course, $\rho_\text{s} < \rho_\text{c}$).
Then the mass $M$ of the planet is the sum of the masses of its core and shell:
$M = V_\text{c} \rho_\text{c} + V_\text{s} \rho_\text{s} = 4/3 \pi R_\text{c}^3 \rho_\text{c} + (4/3 \pi R^3 - 4/3 \pi R_\text{c}^3) \rho_\text{s} = 4/3 \pi R^3 [\rho_\text{s} + \chi^3 (\rho_\text{c} - \rho_\text{s})]$,
where I have defined the ratio of radii as $\chi = R_\text{c}/R$.
We know that for a Star Wars planet
$M/R^2 = g/G$.
Thus
$g/G = 4/3 \pi R [\rho_\text{s} + \chi^3 (\rho_\text{c} - \rho_\text{s})]$,
from where the ratio of radii of the core and and the planet (shell) is
$\chi(R) = \left(\frac{-3 g/G + 4 \pi R \rho_\text{s}}{4 \pi R ( \rho_\text{s}-\rho_\text{c})}\right)^{\frac{1}{3}}$..
Let’s plot the relationship for $\rho_\text{s} = 4000 \text{kg/m}^3$ and $\rho_\text{c} = 20000 \text{ kg/m}^3$.
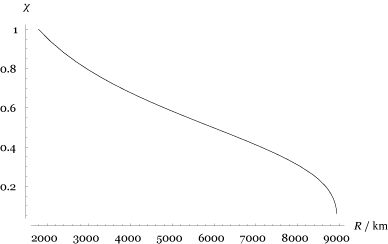
The ratio $\chi$ of the core and plane as function of the radius $R$ of the planet, if the acceleration to to gravity on the surface of the planet is held at $g$.
From the figure we see that with the help of this trick, we can make planets whose radius is as small as $1800 \text{ km}$ or as large as $8800 \text{ km}$. (The actual range is smaller, as it is a rough estimation.)
To further increase the radius of a planet, while keeping $g$ constant, an ice shell may be added. The density of ice is about $1000 \text{ kg/m}^3$ (larger under a great pressure). In this way, the $8800 \text{ km}$ limit can be passed.