Peatükk 4 Alamprogrammid

Põhimõistete peatükis vaatlesime liittüüpe kui suurte andmemahtude korrastamise vahendit. Käesolevas peatükis tutvume alamprogrammidega, mida võib analoogiliselt vaadelda kui suurte koodimahtude struktureerimise ja organiseerimise vahendit.

4.1 Alamprogrammi mõiste

Alamprogrammiks (ingl subroutine) nimetatakse programmilõiku, mis on mõeldud korduvaks kasutamiseks programmi teiste osade poolt. Tavaliselt sooritab alamprogramm ühte suhteliselt terviklikku tegevust, mille määravad alamprogrammi eel- ja järeltingimus.

Alamprogrammi kasutamine koosneb kaht liiki konstruktsioonidest:

ühekordsest alamprogrammi kirjeldusest;
ühe- või mitmekordsest alamprogrammi väljakutsest.

Alamprogrammi kirjeldus seob alamprogrammi nime (madalkeeles aadressi) ja selle sisuks olevad tegevused, kuid ei soorita neid tegevusi. Alamprogrammi kirjeldus kuulub seega deklaratsioonide hulka.

Alamprogrammi väljakutse on juhtkonstruktsioon, mis nõuab, et väljakutse kohas tuleb sooritada eelnevas kirjelduses selle alamprogrammi sisuks märgitud tegevused.

Esimeses lähenduses (mis tegelikult pole päris õige) võib kujutleda, et translaator asendab alamprogrammi väljakutse lause selle alamprogrammi sisuks olevate lausetega.

Alamprogrammid pole sugugi programmeerijate leiutatud. Näiteks võib kokaraamatus esineda tegevusjuhis kujul ``...piruka jaoks tuleb kõigepealt valmistada pärmitaigen (vt põhiretsept lk X)...''. Tegemist on tüüpilise alamprogrammi väljakutsega ja leheküljel X olev pärmitaigna retsept on selle alamprogrammi kirjeldus.

4.1.1 Voorused

Alamprogrammide kasutamisel on mitmeid voorusi:

programm on loetavam --- kui igal alamprogrammil on selle sisule vastav nimi, on põhiprogrammist palju lihtsam aru saada, sest programmi üldise ehitusega tutvumisel ei pea kohe kõiki selle detaile haarama;
programm on testitavam --- kui igal alamprogrammil on selge ülesanne ning eel- ja järeltingimus, on võimalik iga alamprogramm eraldi tõestada või testida enne kui neid omavahel ühtsesse süsteemi ühendama ja siis sellest süsteemist kui tervikust vigu otsima hakata;
programm on hallatavam --- kui sama tegevuse korduvaks sooritamiseks tuleks vastavat programmiosa tekstina mitmesse kohta kopeerida, peaks hiljem sellest osast vigade avastamisel neid vigu igas koopias eraldi parandama; see on asjata lisatöö, pealegi tekib oht, et mõni koopia jääb parandamisel vahele.

4.1.2 Metoodika

Alamprogramme sisaldava programmi kirjutamisele võib läheneda vähemalt kahel põhimõtteliselt erineval viisil.

Ülalt alla arendus

Ülalt alla (ingl top-down) arenduse korral jagatakse lahendatav ülesanne alamülesanneteks ja kirjeldatakse tervikülesande lahendus alamlahenduste kombinatsioonina.

Sellise lähenemise korral algab struktuurse programmi kirjutamine põhiprogrammist, milles alamülesannete lahendamise sammud vormistatakse (sel hetkel veel puuduvate) alamprogrammide väljakutsetena ja hiljem lisatakse vajalike alamprogrammide kirjeldused (võimalik, et need tekitavad omakorda vajaduse uute veel madalama taseme alamprogrammide järele).

Sellist järjest detailsema taseme alamprogrammide kirjutamist jätkatakse seni, kuni kõigi alamülesannete lahendused on välja kirjutatud kasutatava programmikeele primitiivide täpsuseni.

Ülalt alla arenduse üks olulisemaid puudujääke on see, et programmi kõiki osi ei saa kohe nende kirjutamise järel testida --- kui põhiprogrammi kasutatavad alamprogrammid on veel kirjutamata, ei saa põhiprogrammi käima panna.

Alt üles arendus

Alt üles (ingl bottom-up) arenduse korral vaadeldakse alamprogrammide kirjutamist kui kasutatava programmikeele primitiivide hulga laiendamist ülesande lahendamiseks sobivas suunas. Sellist lähenemist õigustab ka asjaolu, et sageli on programmikeele standardsed primitiivid realiseeritud just alamprogrammidena.

Alt üles arenduse kõige suurem raskus on vajadus prognoosida, milliseid uusi primitiive ülesande lahendamiseks tegelikult vaja läheb. Ilma sellise prognoosita on oht kulutada palju aega sellele, et kirjutada alamprogramme, mida lõpuks üldse vaja ei lähe ja unustada esimesel lähenemisel kirjutada mõned, mis hiljem vajalikuks osutuvad.

Kombineeritud arendus

Kahe eelpool kirjeldatud ``puhta'' arendusmetoodika puudujääkide leevendamiseks jagatakse programmi kirjutamine tavaliselt kaheks etapiks.

Projekteerimise etapil lähenetakse ülesande lahendamisele ülalt alla meetodil ja jagatakse selle lahendus ilma programmi kirjutamata (ja sageli isegi konkreetset programmikeelt valimata) alamülesanneteks eesmärgiga saada teada, milliseid alamprogramme on selle ülesande lahendamiseks vaja ja kuidas need alamprogrammid omavahel seotud olema peaks.

Realiseerimise etapil hakatakse vajalikke alamprogramme kirjutama alt üles meetodil, sest nii on iga alamprogrammi valmimise ajaks olemas ka kõik need, mida ta oma tööks kasutab ja seetõttu on võimalik iga alamprogrammi kohe pärast tema kirjutamist testida.

Illustratsiooniks koostame lihtsa algoritmi kõigi algarvude leidmiseks etteantud lõigust L = a ... b.¹

Projekteerimise etapil paneme tähele, et kõige ilmsem lahendus on kontrollida iga lõiku L jääva arvu kohta, kas ta on algarv, ja väljastada need arvud, mille korral kontrollimine annab positiivse tulemuse.

Kuna üldotstarbelistes programmikeeltes enamasti algarvulisuse kontrollimise primitiivi pole, peame selle ise realiseerima. Kõige lihtsam lahendus on proovida kontrollitavat arvu kõigi temast väiksemate ja ühest suuremate täisarvudega jagada; täpse jagumise korral on tegemist kordarvuga, kui aga jagamine ühegi arvuga ei õnnestu, on tegemist algarvuga.

Realiseerimise etapil alustame altpoolt, algarvulisuse kontrollimise alamprogrammist. Kohe pärast selle alamprogrammi kirjutamist saame tõestada tema aluseks oleva algoritmi õigsuse ja testida selle realiseerimise korrektsust. Alles siis, kui algarvulisuse kontrollimise alamprogramm on valmis ja kontrollitud, liigume edasi põhiprogrammi juurde.

4.1.3 Protseduur ja funktsioon

Enamik tänapäevaseid programmikeeli eristavad protseduure ja funktsioone.

Funktsiooniks (ingl function) nimetatakse alamprogrammi, mis tagastab oma töö tulemusena mingi väärtuse. Funktsioonil on tüüp --- funktsioon tagastab ainult sellesse tüüpi kuuluvaid väärtusi --- ja funktsiooni väljakutset võib kasutada avaldises seda tüüpi operandina.

Protseduuriks (ingl procedure) nimetatakse alamprogrammi, mis ei ole funktsioon. Protseduur ei tagasta otseselt mingit väärtust ja seetõttu ei saa protseduuri väljakutset operandina kasutada.

Selle erinevuse illustreerimiseks vaatleme näiteks paljudes programmikeeltes protseduurina realiseeritud primitiivi antud sõne väljastamiseks ja peaaegu kõigis keeltes funktsioonina realiseeritud primitiivi antud reaalarvu siinuse arvutamiseks.

Kuna sõne väljastamise primitiiv on protseduur, võib selle väljakutset kasutada lihtlausena, näiteks

väljasta `Tere, kasutaja'

Kuna siinuse arvutamine on funktsioon, võib selle väljakutset kasutada operandina avaldises, näiteks

z¬sin(x)+sin(y)+1

Edaspidises kasutame alamprogrammide kirjeldamiseks esimeses peatükis kasutusele võetud pseudokeelt, lisades igale algoritmile nime, mille abil on võimalik sellele hiljem mujalt viidata.

Näiteks protseduuri 1 ja 100 vahele jäävate algarvude väljastamiseks võiks esitada algoritmis 1 toodud kujul, kus OnAlgarv tähistab (veel kirjutamata) funktsiooni muutuja a väärtuse algarvulisuse kontrollimiseks.

Algoritm 1 AlgarvudSajani: Väljastab algarvud lõigust 1 ... 100
Abimuutujad: a Î N --- jooksev algarvukandidaat

korda a¬1 ... 100
kui OnAlgarv
väljasta a
lõppkui
lõppkorda

Funktsiooni väärtuse põhiprogrammile tagastamise käsu süntaks on erinevates programmikeeltes erinev, oma pseudokeeles kasutame edaspidi lauset kujul

tagasta v

kus v on funktsiooni väljakutse väärtus põhiprogrammi avaldises.

Funktsiooni muutuja a jooksva väärtuse algarvulisuse kontrollimiseks võime seega esitada nii, nagu näha algoritmis 2.

Algoritm 2 OnAlgarv: Kontrollib, kas muutuja a väärtus on algarv
Sisend: a Î N --- uuritav väärtus
Väljund: tõene, kui a on algarv, väär vastasel juhul
Abimuutujad: j Î N --- jooksev jagajakandidaat

kui a < 2
--- vähim algarv on 2
tagasta väär
lõppkui
korda j¬2 ... a-1
kui a / j Î N
--- leidsime jagaja, järelikult kordarv
tagasta väär
lõppkui
lõppkorda
--- ei leidnud jagajat, järelikult algarv
tagasta tõene

4.1.4 Deklaratsioon ja definitsioon

Paljudes keeltes eristatakse alamprogrammi deklaratsiooni ja definitsiooni.

Alamprogrammi deklaratsioon (ingl declaration) fikseerib selle välise liidese --- nime, parameetrite arvu ja nende tüübid ning funktsiooni korral ka tagastatava väärtuse tüübi ---, kuid ei sisalda alamprogrammi sisuks olevaid käske; definitsioon (ingl definition) sisaldab ka alamprogrammi sisu, kuid mõnes keeles pole deklaratsiooni olemasolu korral parameetrite kirjelduse kordamine enam vajalik.

Neid mõisteid eristatakse tavaliselt üsna tehnilistel (ja erinevates keeltes veidi erinevatel) põhjustel, seetõttu me neil pikemalt ei peatu.²

4.2 Alamprogrammi lokaalsed muutujad

Suures programmis, mis koosneb paljudest alamprogrammidest, võib kergesti juhtuda, et mitme alamprogrammi autorid tahavad kasutada samade nimedega abimuutujaid. See on aga ohtlik, sest sellisel juhul võib ühe alamprogrammi kasutamine rikkuda teise tööks vajalikud andmed.³

Ohu vähendamiseks (ja ka muudel põhjustel) võimaldavad tänapäevased programmikeeled kasutada mitme erineva skoobi ja elueaga muutujaid.

4.2.1 Muutuja eluiga

Muutuja elueaks (ingl lifetime) nimetatakse programmi osa, mille täitmise ajal see muutuja oma väärtust säilitab.

Kuna muutuja väärtust hoitakse mälus, siis peab ta oma eluea vältel mingit mäluosa oma valduses hoidma.

Eluea järgi võib muutujad jagada kolme liiki:

staatilise (ingl static) muutuja eluiga on kogu programmi täitmise aeg; talle eraldatakse mälu programmi käivitamise hetkel ja see mälu jääb tema kasutusse kuni programmi täitmise lõpuni; muutujale kord omistatud väärtus püsib alles kuni järgmise omistamiseni;
automaatse (ingl automatic) muutuja eluiga on tavaliselt mingi alamprogrammi ühe täitmise aeg; automaatne muutuja luuakse (talle eraldatakse mälu) alamprogrammi täitmise alguses ja ta hävitatakse (talle eraldatud mälu vabastatakse) selle täitmise lõppedes; alamprogrammi järgmisel täitmisel võidakse selle muutuja hoidmiseks kasutada hoopis teist mälupesa, seega automaatse muutuja väärtus alamprogrammi kahe täitmiskorra vahel ei säili;
dünaamiline (ingl dynamic) muutuja luuakse ja hävitatakse programmeerija otsese käsu peale, seega on dünaamilise muutuja eluiga täielikult programmeerija määrata.⁴

4.2.2 Muutuja skoop

Muutuja skoobiks (ingl scope) nimetatakse programmi osa, milles selle muutuja nimi nähtav on.

Muutuja nimega pole suurt midagi peale hakata, kui sellele ei vasta mälupesa, milles muutuja väärtust hoida. Sellepärast ongi muutuja skoop tavaliselt tema eluea alamhulk.

Skoobi järgi võib muutujad jagada kahte liiki:

globaalseks (ingl global) nimetatakse muutujat, mis on kirjeldatud väljaspool kõiki alamprogramme;

Selline muutuja on üldiselt nähtav kõigile programmi osadele, seega on alati oht, et keegi teine võib selle väärtust muuta. Sellepärast tuleks globaalseid muutujaid kasutada nii vähe kui võimalik.

Globaalsed muutujad on tavaliselt staatilised.
lokaalseks (ingl local) nimetatakse muutujat, mis on kirjeldatud mingi alamprogrammi sees;

Selline muutuja ei ole sama programmi teistele osadele otse kättesaadav ja seega ei saa keegi kogemata seda muutujat kasutades tema väärtust rikkuda.

Tavaliselt on lokaalsed muutujad automaatsed, aga mõned programmikeeled võimaldavad luua ka staatilisi lokaalseid muutujaid.⁵

Staatiliste lokaalsete muutujate abil saab kirjutada alamprogramme, mis uuel kasutamisel ``mäletavad'', mida nad eelmisel korral tegid. See võib olla kasulik näiteks siis, kui alamprogrammi esimesel käivitamisel arvutatakse välja mingid abitulemused, mida läheb vaja ka järgmistel käivitamiskordadel.

4.3 Alamprogrammi parameetrid

Alamprogrammide kasutamine oleks üsna tüütu, kui vastaks tõele peatüki alguses antud lihtsustatud kujutlus, mille kohaselt translaator asendab alamprogrammi väljakutse lause mehhaaniliselt selle alamprogrammi kirjelduses olevate lausetega.

Oletame, et meil on vaja kirjutada alamprogramm, mis väljastab mistahes arvu ruudu. Kui alamprogrammi väljakutse oleks tõesti vaid mehhaaniline tekstiasendus, oleks meil vaja kirjutada eraldi alamprogrammid kõigi võimalike arvude ruutude väljastamiseks või luua ruutu tõstetava arvu edastamiseks globaalne muutuja ja omistada enne alamprogrammi väljakutsumist sellele muutujale vajalik väärtus (sisuliselt sama võtet kasutasime muutuja a väärtuse edastamisel algarvude arvutamise programmis).

Et kumbki variant pole kasutamiseks kuigi mugav --- esimene neist on ilmselt võimatu, teise puhul hakkaks suuremates programmides (milles on palju alamprogramme ja neil omakorda palju parameetreid) tekkima massiliselt globaalseid muutujaid ---, lubavad kõik tänapäevased programmikeeled kasutada alamprogrammides parameetreid.

4.3.1 Formaalsed ja tegelikud parameetrid

Parameetrite alamprogrammile edastamise aparaat koosneb formaalsetest ja tegelikest parameetritest.

Formaalsed parameetrid (ingl formal parameter) on alamprogrammi definitsioonis kasutusel selleks, et anda parameetritele nimed, millega on võimalik alamprogrammi sisuks olevates käskudes osutada, millal ja kuidas alamprogramm talle parameetritena antavaid väärtusi kasutab. Alamprogrammi väljakutsel sellele töötlemiseks antavaid väärtusi nimetatakse tegelikeks parameetriteks (ingl actual parameter).

Formaalse parameetri mõiste illustreerimiseks oletame, et üks sõber kingib teisele loteriipileti ja küsib ``mida Sa teed, kui võidad?''. Kui kingi saaja vastab midagi stiilis ``kui võit on väike, ostan maiustusi, aga kui suur, siis peab mõtlema'', on ta sellega defineerinud parameetriga algoritmi, mis kirjeldab tema käitumist võidu korral vastavalt võidu suurusele. Võidu suurus on selle algoritmi formaalne parameeter --- sest tegelikult selle plaani järgi tegutsema hakata ei saa muidugi enne kui võit tõesti käes on.

Olukord on veelgi sarnasem matemaatikatunnist tuntud funktsioonidega. Funktsiooni f kirjelduses kujul f(x)=2x+1 on x formaalne parameeter, mida kasutatakse selleks, et avaldises 2x+1 näidata, kuidas f oma parameetrit kasutab. Avaldises f(3)+f(4) on arvud 3 ja 4 aga funktsiooni f tegelikud parameetrid selle kahel kasutamisel, kusjuures f(3)+f(4) tähistab muidugi avaldist (2·3+1)+(2·4+1).

Mitme parameetriga alamprogrammides seatakse tegelikke ja formaalseid parameetreid tavaliselt vastavusse samamoodi kui mitme muutuja funktsioonides matemaatikas --- alamprogrammi väljakutsel esitatakse kõik tegelikud parameetrid järjest ja selles järjestuses esimene tegelik parameeter loetakse alamprogrammi esimese formaalse parameetri väärtuseks, teine tegelik parameeter teise formaalse parameetri väärtuseks jne.⁶

Lisaks formaalsete parameetrite nimedele nõuavad paljud keeled ka nende tüüpide kirjeldamist. See võimaldab translaatoril kontrollida, et parameetritena edastatavate väärtuste kasutamine vastab nende väärtuste tüüpidele.⁷ Programmi transleerimisel toimub parameetrite tüübikorrektsuse kontroll tavaliselt kahe sammuna: alamprogrammi definitsiooni transleerimisel kontrollib translaator, et parameetrite kasutamine alamprogrammi sisuks olevates käskudes on kooskõlas formaalsete parameetrite deklareeritud tüüpidega --- iga parameetriga sooritatavad operatsioonid peavad kõik kuuluma selle parameetri tüübi operatsioonivarusse; alamprogrammi väljakutse transleerimisel kontrollib translaator, et tegelike parameetritena antud väärtuste tüübid vastavad formaalsete parameetrite deklareeritud tüüpidele.

4.3.2 Sisend- ja väljundparameetrid

Alamprogrammide parameetrid võib nende kasutuseesmärgi alusel jagada sisend- ja väljundparameetriteks.

Sisendparameetrid (ingl input parameter), nagu nimestki oletada võib, on mõeldud lähteandmete edastamiseks alamprogrammi väljakutsujalt sellele alamprogrammile.

Näiteks siinusfunktsioonile antav nurga suurus on sisendparameeter. Ka väljastamisprimitiivile (mis on paljudes programmeerimissüsteemides realiseeritud alamprogrammina) väljastamiseks antav suurus on selle primitiivi seisukohalt sisendparameeter --- selle kaudu saab primitiiv andmed, mida ta töötlema (antud juhul väljastama) peab.

Väljundparameetrid (ingl output parameter) seevastu on mõeldud tulemuste tagastamiseks alamprogrammilt selle väljakutsujale.

Näiteks sisestamisprimitiivile parameetrina antav muutuja on väljundparameeter --- primitiiv ei vaja selle muutuja esialgset väärtust (muutuja võib olla ka algväärtustamata), vaid kasutab teda ainult kohana kasutajalt või failist saadud andmete salvestamiseks.

Ka funktsiooni tagastatavat väärtust võib vaadelda väljundparameetrina, kujutledes, et translaator tekitab ajutise muutuja ja kasutab funktsiooni poolt sellesse muutujasse salvestatud tulemust avaldises funktsiooni väljakutse väärtusena.

Sageli on üks parameeter kasutusel nii sisend- kui väljundparameetrina. Näiteks kui arvumassiivi sorteerimise alamprogramm saab töödeldava massiivi ette parameetrina, siis on see kasutusel nii sisendparameetrina (selle kaudu edastatakse alamprogrammile järjestamist vajavad elemendid) kui ka väljundparameetrina (selle kaudu tagastatakse alamprogrammist massiivi uus sisu, milleks on needsamad elemendid vajalikus järjekorras).

4.3.3 Väärtus- ja muutujaparameetrid

Kuigi eelmises jaotises kirjeldatud parameetrite liigitus on mugav algoritmi koostaja mõtte väljendamiseks, kasutatakse programmikeeltes realiseerimise efektiivsuse huvides veidi teistsugust klassifikatsiooni.

Väärtusparameetri (ingl call by value) kasutamisel leiab süsteem alamprogrammi käivitamisel tegeliku parameetrina antud avaldise paremväärtuse ja edastab alamprogrammile selle. Muidugi saab niimoodi kasutada ainult avaldist, millel on paremväärtus olemas.

Alamprogramm võib saadud parameetrit kasutada nagu algväärtustatud lokaalset muutujat. See tähenab, et kui alamprogramm sellele ``lokaalsele muutujale'' uue väärtuse omistab, kehtib uus väärtus ainult alamprogrammi sees ja ei mõjuta põhiprogrammi avaldist.

Eelnevast järeldub, et väärtusparameetrite mehhanismi on võimalik kasutada ainult alamprogrammide sisendparameetrite realiseerimiseks --- kui alamprogrammis olev väärtus on põhiprogrammi avaldisest täielikult lahutatud, pole selle kaudu kuidagi võimalik andmeid alamprogrammist põhiprogrammile tagastada.

Muutujaparameetri (ingl call by reference) kasutamisel edastatakse alamprogrammile parameetrina antud avaldise vasakväärtus --- tavaliselt on sellise parameetrina kasutusel põhiprogrammi muutuja (millest tuleb ka parameetrite edastamise viisi eestikeelne nimetus), kuigi võib kasutada ka kõiki muid avaldisi, millel on vasakväärtus olemas.

Muutujaparameetrile alamprogrammis omistatud uus väärtus muudab ka põhiprogrammi muutuja väärtuse, seega on muutujaparameetrite mehhanismi võimalik kasutada ka väljundparameetrite realiseerimiseks.

Kuna väärtusparameetrist alamprogrammi jaoks koopia tegemine kulutab nii aega kui mälu, edastatakse praktikas suuremahulisi väärtusi muutujaparameetritena ka siis, kui algoritmi loogika seisukohalt on tegemist alamprogrammi sisendparameetritega. Mõnes keeles on olemas isegi eraldi konstruktsioon väljendamaks, et alamprogramm talle antud muutujaparameetri väärtust ei muuda (see tähendabki, et sisuliselt kasutab alamprogramm seda sisendparameetrina).

Nimiparameetri (ingl call by name) kasutamisel edastab süsteem alamprogrammile parameetrina antud avaldise enda, ilma selle väärtust arvutamata. Kui alamprogrammil on avaldise väärtust (ükskõik, kas vasak- või paremväärtust) vaja, peab ta selle ise leidma.

Nimiparameetreid on hea kasutada näiteks siis, kui alamprogramm ei vaja igal käivitamisel kõigi oma parameetrite väärtusi ja mõne väärtuse leidmine võib olla väga töömahukas --- sellisel juhul on otstarbekam arvutada parameetri väärtus välja alles siis, kui on kindel, et seda tõesti vaja läheb.

Parameetrite sellist kohtlemist nimetatakse laisaks väärtustamiseks (ingl lazy evaluation), vastandina agarale väärtustamisele (ingl eager evaluation). Mõned programmikeeled väärtustavad laisalt kõiki avaldisi, mitte ainult alamprogrammide parameetreid.⁸

4.4 Rekursioon

4.4.1 Rekursiooni mõiste

Alamprogrammide tähtis rakendus on rekursiivsete algoritmide programmeerimine. Algoritmi nimetatakse rekursiivseks (ingl recursive), kui selles kasutatakse ühe (või ka mitme) sammuna sama algoritmi ennast. Selle määratluse põhjal võib rekursiooni olemus jääda üsna arusaamatuks, sestap vaatleme lihtsa näitena naturaalarvu faktoriaali arvutamist.

Eelmises peatükis defineerisime arvu n faktoriaali n! valemiga

n! =

ì
í
î

1,	kui n = 0,
1 · 2 · ... · n,	kui n > 0.

Selle definitsiooni järgimisel on kõige loomulikum tulemus järgmine korduslauset kasutav algoritm:

Algoritm 3 Fakt1: Leiab antud naturaalarvu faktoriaali
Sisend: n Î N
Väljund: tagastab n!
Abimuutujad: i, f

f¬1
korda i¬1 ... n
--- vahetingimus: f = (i - 1)!
f¬f * i
--- vahetingimus: f = i!
lõppkorda
tagasta f

Faktoriaali võib lisaks eelpool vaadeldud valemile defineerida ka seosega

n! =

ì
í
î

1,	kui n = 0,
n · (n - 1)!,	kui n > 0.

Selle definitsiooni järgimine annab meile rekursiivse algoritmi:

Algoritm 4 Fakt2: Leiab antud naturaalarvu faktoriaali
Sisend: n Î N
Väljund: tagastab n!

kui n = 0
tagasta 1
muidu
tagasta n * Fakt2(n - 1)
lõppkui

Selle algoritmi täitmine näiteks 3! arvutamiseks toimub järgmiselt:

alamprogrammi kasutaja (tavaliselt programmi mõni teine osa) käivitab Fakt2(3);

süsteem loob alamprogrammi Fakt2 esimese eksemplari ja hakkab seda täitma; kuna n = 3 ¹ 0, asub süsteem alamprogrammi kehas täitma valikulause muidu-haru; avaldise 3 * Fakt2(2) arvutamine käivitab Fakt2(2);

süsteem loob alamprogrammi Fakt2 teise eksemplari ja hakkab seda täitma; kuna n = 2 ¹ 0, asub süsteem alamprogrammi kehas täitma valikulause muidu-haru; avaldise 2 * Fakt2(1) arvutamine käivitab Fakt2(1);

süsteem loob alamprogrammi Fakt2 kolmanda eksemplari ja hakkab seda täitma; kuna n = 1 ¹ 0, asub süsteem alamprogrammi kehas täitma valikulause muidu-haru; avaldise 1 * Fakt2(0) arvutamine käivitab Fakt2(0);

süsteem loob alamprogrammi Fakt2 neljanda eksemplari ja hakkab seda täitma; kuna n = 0, tagastab süsteem Fakt2(0) väärtusena 1;

süsteem lõpetab 1 * Fakt2(0) arvutamise ja tagastab Fakt2(1) väärtusena 1 · 1 = 1;

süsteem lõpetab 2 * Fakt2(1) arvutamise ja tagastab Fakt2(2) väärtusena 2 · 1 = 2;

süsteem lõpetab 3 * Fakt2(2) arvutamise ja tagastab Fakt2(3) väärtusena 3 · 2 = 6.

4.4.2 Programmi magasin

Rekursiooni mõistmiseks peame kõigepealt loobuma peatüki alguses kasutusele võetud lihtsustatud kujutlusest alamprogrammide käivitamise mehhaanika kohta ja tegema endale selgeks, kuidas asjad tegelikult käivad.

Alamprogrammi käivitamisel luuakse aktiveerimiskirje (ingl activation record). Iga alamprogrammi iga eksemplari kohta luuakse uus kirje, mis iseloomustab alamprogrammi just seda käivitamist. Tavaliselt on selles kirjes kolme liiki andmed:

alamprogrammile edastatavad tegelikud parameetrid;
ruum alamprogrammi lokaalsete muutujate jaoks;
naasmisaadress (ingl return address) --- informatsioon selle kohta, millisest käsust tuleb jätkata pärast alamprogrammi täitmise lõppu.

Eelmises lõigus toodud näites oleks väljakutse Fakt2(2) aktiveerimiskirje sisu selline:

tegelikud parameetrid: n = 2;
lokaalsed muutujad: pole;
naasmisaadress: korrutamistehe avaldises n * Fakt2(n - 1).

Rekursiooni toimimise jaoks on oluline, et neid aktiveerimiskirjeid võib ühe alamprogrammi jaoks olla mitu --- kui iga alamprogrammi iga eksemplari parameetrid ja lokaalsed muutujad on omaette kirjes, võib korraga olla pooleli ühe alamprogrammi mitme eksemplari täitmine ilma et need üksteist segaks. Parasjagu pooleliolevate alamprogrammide aktiveerimiskirjeid hoitakse programmi kutsemagasinis (ingl call stack).⁹

Alamprogrammi ühe eksemplari töö lõppedes kustutatakse selle eksemplari aktiveerimiskirje ära ja vabanenud mälu võib süsteem kasutada nii selle kui ka teiste alamprogrammide uute eksemplaride loomiseks.

Magasini töö illustreerimiseks vaatleme veidi keerulisemat rekursiivset algoritmi, nimelt Hanoi tornide ülesande lahendust.

Ülesanne on järgmine: on kolm varrast, neist ühel n erineva suurusega ketast suuruse järjekorras (suurim all); vaja on kõik need kettad viia teisele vardale, kusjuures tõsta tohib ainult ühte ketast korraga; kolmandat varrast võib kasutada ajutise hoiukohana, kuid ühelegi vardale ei tohi panna suuremat ketast väiksema peale. Selle ülesande (üks võimalik) lahendus n = 3 jaoks on toodud joonisel 4.1.

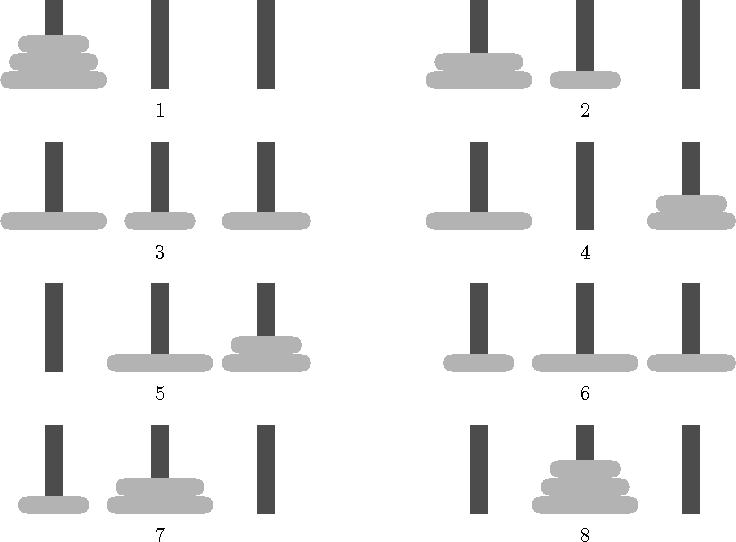
Joonis 4.1: Hanoi tornid, n = 3

Hanoi tornide ülesannet on võimalik lahendada ka rekursiooni kasutamata, kuid rekursiivse algoritmi leidmine on palju lihtsam: selleks, et me saaks tõsta suurima ketta esimeselt vardalt teisele, peame enne kõik väiksemad kettad kolmandale vardale viima --- kui mõned neist oleks esimesel vardal, ei saaks me suurimat ketast nende alt kätte; kui mõned neist oleks teisel vardal, et tohiks me suurimat ketast nende peale panna. Pärast suurima ketta teisele vardale tõstmist peame ka väiksemad kettad kolmandalt vardalt teisele viima. Osutub, et ülesande lahendus ongi täpselt nii lihtne:

Algoritm 5 Hanoi: Lahendab Hanoi tornide ülesande
Sisend: n Î N --- ketaste arv; kust, kuhu, abi Î {A,B,C}

kui n > 0
Hanoi(n - 1, kust, abi, kuhu) --- pealmised kettad lähtekohast abivardale
väljasta kust, `®', kuhu --- alumine ketas lähtekohast sihtkohta
Hanoi(n - 1, abi, kuhu, kust) --- pealmised kettad abivardalt sihtkohta
lõppkui

Selle algoritmi täitmine näiteks 2 ketta viimiseks vardalt A vardale B toimub järgmiselt (märkide á ja ñ vahel on toodud programmi magasini seis):

alamprogrammi kasutaja käivitab Hanoi(2,A,B,C);

süsteem loob Hanoi esimese eksemplari;
áHanoi(2,A,B,C)ñ;
kuna n = 2 > 0, käivitatakse Hanoi(1,A,C,B);

süsteem loob Hanoi teise eksemplari;
áHanoi(2,A,B,C),Hanoi(1,A,C,B)ñ;
kuna n = 1 > 0, käivitatakse Hanoi(0,A,B,C);

süsteem loob Hanoi kolmanda eksemplari;
áHanoi(2,A,B,C),Hanoi(1,A,C,B),Hanoi(0,A,B,C)ñ;
kuna n = 0, lõpetab Hanoi kolmas eksemplar oma töö kohe;

áHanoi(2,A,B,C),Hanoi(1,A,C,B)ñ;
jätkub Hanoi teise eksemplari täitmine: tõstetakse üks ketas vardalt A vardale C ja käivitatakse Hanoi(0,B,C,A);

süsteem loob Hanoi uue kolmanda eksemplari;
áHanoi(2,A,B,C),Hanoi(1,A,C,B),Hanoi(0,B,C,A)ñ;
kuna n = 0, lõpetab Hanoi kolmas eksemplar oma töö kohe;

áHanoi(2,A,B,C),Hanoi(1,A,C,B)ñ;
Hanoi teine eksemplar lõpetab oma töö;

áHanoi(2,A,B,C)ñ;
jätkub Hanoi esimese eksemplari täitmine: tõstetakse üks ketas vardalt A vardale B ja käivitatakse Hanoi(1,C,B,A);

süsteem loob Hanoi uue teise eksemplari;
áHanoi(2,A,B,C),Hanoi(1,C,B,A)ñ;
kuna n = 1 > 0, käivitatakse Hanoi(0,C,A,B);

süsteem loob Hanoi kolmanda eksemplari;
áHanoi(2,A,B,C),Hanoi(1,C,B,A),Hanoi(0,C,A,B)ñ;
kuna n = 0, lõpetab Hanoi kolmas eksemplar oma töö kohe;

áHanoi(2,A,B,C),Hanoi(1,C,B,A)ñ;
jätkub Hanoi teise eksemplari täitmine: tõstetakse üks ketas vardalt C vardale B ja käivitatakse Hanoi(0,A,B,C);

süsteem loob Hanoi uue kolmanda eksemplari;
áHanoi(2,A,B,C),Hanoi(1,C,B,A),Hanoi(0,A,B,C)ñ;
kuna n = 0, lõpetab Hanoi kolmas eksemplar oma töö kohe;

áHanoi(2,A,B,C),Hanoi(1,C,B,A)ñ;
Hanoi teine eksemplar lõpetab oma töö;

áHanoi(2,A,B,C)ñ;
Hanoi esimene eksemplar lõpetab oma töö;

áñ.

4.4.3 Rekursiooni õigsus

Eeltoodud näidete põhjal peaks juba silma torkama rekursiivsete algoritmide üldskeem: ülesande mingid lihtsad erijuhud lahendatakse otseselt, keerulisemad aga taandatakse kas ühele või mitmele mingis mõttes lihtsamale juhule ja otsitav tulemus saadakse nende lihtsamate juhtude lahendustest.

Neid lihtsaid erijuhte, mille algoritm otseselt lahendab, nimetatakse rekursiooni baasiks (ingl base) --- nii faktoriaali kui ka Hanoi tornide ülesandes on baasiks juhtum, kui n = 0. Keerulisema juhu lahendamist lihtsamate juhtude kaudu nimetatakse rekursiooni sammuks (ingl step). Nagu eelneva põhjal oodata võibki, tuleb rekursiivse algoritmi õigsuses veendumiseks kontrollida nii baasi kui ka sammu õigsust.

Kuna rekursiooni baasi käsitlemine on ``tavaline'', rekursioonita algoritm, pole selle õigsuses veendumiseks vaja mingeid täiendavaid vahendeid --- kasutada tuleb eelmistes peatükkides tutvustatud tehnikaid. Näiteks Hanoi tornide ülesande lahenduses on ilmne, et baasjuhtum lahendatakse õigesti --- kui n = 0, tuleks ühelt vardalt teisele viia 0 ketast; kuna selleks pole vaja midagi teha, on algoritm, mis ei teegi midagi, ilmselt õige.

Rekursiooni sammu õigsuse tõestamisel eeldame, et alamprogrammi aktiivsest eksemplarist tehtavad väljakutsed selle algoritmi enda poole töötavad õigesti. Rekursiooni sammu õigsuse tõestamiseks on vaja veenduda, et selle eelduse kehtimisel töötab algoritm õigesti. Näiteks Hanoi tornide ülesande lahenduse korral eeldame, et mõlemad rekursiivsed väljakutsed kujul Hanoi(n - 1, ...) toimetavad n - 1 ketast nõutud viisil ühelt vardalt teisele. Sammu õigsuse tõestamiseks peame esiteks tähele panema, et kui me viime n - 1 ketast lähtevardalt abivardale, tõstame viimase (suurima) ketta lähtevardale ja siis viime ka varem kõrvale pandud n - 1 ketast abivardalt sihtvardale, on nende operatsioonide tulemusena tõesti kõik n ketast sihtvardal. Kui meie eeldused rekursiivsete väljakutsete õigsuse kohta kehtivad, on need kettad ka õiges järjekorras.

Aga sellest ei järeldu veel meie algoritmi õigsus. Nimelt tuleb meil lisaks kontrollida, et iga rekursiivse väljakutse eel kehtib meie algoritmi eeltingimus. Seda on muidugi raske teha, kui eeltingimus pole selgelt välja kirjutatud. Seda tingimust pole aga algoritmi 5 kirjelduses välja toodud sellepärast, et esimesena pähetulev sõnastus --- eeltingimus: n ketast vardal kust, ülejäänud kaks varrast tühjad --- on liiga range. Sellest eeltingimusest lähtudes ei võiks me rekursiivseid pöördumisi teha, sest meil on süsteemis üks liigne ketas.

Algoritmi õigsuses veendumiseks tuleb tähele panna, et tegelikult pole meil vaja nii ranget eeltingimust. Piisab sellest, kui me eeldame, et kõik need kettad, mida me oma algoritmi aktiivses eksemplaris ei puutu, on suuremad kui need, mida me liigutame. Tõepoolest, mõnel vardal meie ketastest allpool olev ja neist kõigist suurem ketas ei erine ülesande tingimuste seisukohalt maapinnast --- me võime kõiki teisi kettaid ilma mingite piiranguteta nende peale asetada.

Eelnevast lähtudes saame sõnastada oma lahenduse tegeliku eel- ja järeltingimuse --- eeltingimus: n pealmist ketast vardal kust, kõik ülejäänud kettad kõigil kolmel vardal on suuremad kõigist neist n kettast; järeltingimus: n pealmist ketast vardalt kust viidud nende omavahelist järjekorda säilitades vardale kuhu, kõik muud kettad oma esialgsetel kohtadel. Sellise eel- ja järeltingimuse korral on rekursiooni sammu tõestamine juba lihtne.

Arvatavasti pole isegi selle ühe näite põhjal raske märgata, et rekursiivse algoritmi eeltingimus on natuke sarnane korduse invariandiga. Osutub, et see sarnasus pole juhuslik --- nimelt on mistahes kordust kasutav algoritm võimalik üles kirjutada rekursiooni abil ja tavaliselt on seda teisendust kõige lihtsam teha just korduse invarianti rekursiooni eeltingimusena kasutades.

Rekursioonil ja kordusel on veel üks sarnasus --- mõlemad võimaldavad koostada algoritme, mis jäävad lõpmatuseni tööle. Nagu korduse, nii ka rekursiooni puhul tõestab eel- ja järeltingimuste vaatlemine ainult algoritmi osalise õigsuse --- kui see algoritm oma töö lõpetab, saame nõutud tulemuse. Tegelikult huvitab meid muidugi täielik õigsus --- me tahame olla kindlad, et see tore hetk mingi lõpliku aja jooksul kätte jõuab.

Rekursiivse algoritmi puhul tähendab see, et me peame näitama, et mistahes lubatud algandmetest alustades jõuame mingi lõpliku arvu sammude järel välja rekursiooni baasini. Näiteks algoritmide 4 ja 5 puhul on selles veendumine triviaalne: kuna rekursiooni baas on n = 0 ja igal rekursiivsel pöördumisel vähendame n väärtust 1 võrra, jõuame n mistahes naturaalarvulisest väärtusest alustades baasjuhuni täpselt n sammu järel.

Kokkuvõtteks, rekursiivse algritmi koostamisel peame

valima selle eel- ja järeltingimused nii, et need võimaldaks kasutada sama algoritmi ülesande mingite väiksemate osade lahendamiseks;
valima mingid (soovitavalt lihtsad) baasjuhud, mille algoritm lahendab otseselt ja tõestama nende juhtude lahenduse õigsuse;
taandama kõik ülejäänud juhud lihtsamate juhtude lahendamisele ja näitama, et taandamisel saadud lihtsamad juhud rahuldavad algoritmi eeltingimusi ja nende lihtsamate juhtude lahendustest koostatud lahendus rahuldab algoritmi järeltingimust;
veenduma, et iga lubatud juht oleks kas baasjuht või taanduks baasjuhule mingi lõpliku arvu sammude järel.

Algoritmide 4 ja 5 jaoks oleme praeguseks kõik eeltoodud nõuded rahuldanud, seega võime nende õigsuse tõestatuks lugeda.

Ülesanded

Ülesanne 1 Kirjutada õppematerjali lisas toodud algarvude arvutamise programmis protseduur AlgarvudSajani ümber funktsiooniks, mis algarvude ekraanile väljastamise asemel tagastab nende summa.

Ülesanne 2 Muuta sama programmi nii, et funktsioon OnAlgarv saab uuritava väärtuse parameetrina ja seejärel kaotada programmist globaalne muutuja a.

Ülesanne 3 Asendada samas programmis AlgarvudSajani funktsiooniga AlgarvudAB, mis saab parameetritena kaks täisarvu a ja b ning summeerib algarvud lõigus a ... b. Uuritava lõigu otspunktid pärida kasutajalt.

Ülesanne 4 Naturaalarvu n poolfaktoriaal n!! defineeritakse järgmiselt:

n!! =

ì
í
î

1,	kui n = 0,
1 · 3 · ... · n,	kui n > 0 ja n on paaritu,
2 · 4 · ... · n,	kui n > 0 ja n on paaris.

Kirjutada poolfaktoriaalide arvutamiseks kaks funktsiooni: üks korduse ja teine rekursiooni abil. Tõestada mõlema õigsus. Kontrollida mõlema tööd ka piirjuhtudel (n Î {0, 1, 2}).

Ülesanne 5 Algoritmi 5 järgi töötav programm teeb massiliselt alamprogrammi Hanoi väljakutseid, kus n = 0. Kuna alamprogramm sellisel juhul mingit kasulikku tööd ei tee, kulutab süsteem ilmaasjata aega selle alamprogrammi uute eksemplaride loomisele ja kustutamisele. Muuta algoritmi nii, et selliseid asjatuid väljakutseid ei oleks --- see tähendab, kirjutada algoritm, milles baasjuht oleks n = 1. Tõestada uue versiooni õigsus.

Ülesanne 6 Fibonacci jada defineeritakse järgmise seosega:

F_i =

ì
í
î

1,	kui i = 0 või i = 1,
F_i-1 + F_i-2,	kui i > 1.

Kirjutada antud järjekorranumbrile vastava Fibonacci jada liikme arvutamiseks kaks funktsiooni: üks rekursiooni ja teine korduse abil. Tõestada mõlema õigsus.

Võrrelda (katseliselt) nende funktsioonide töökiirusi parameetri i erinevatel väärtustel. Kas oskate kirjutada rekursiivse funktsiooni, mis töötab sama kiiresti kui kordust kasutav? (Viimane pole koduse töö kohtususlik osa.)

1: Olgu kohe märgitud, et see algoritm on oma lihtsuse tõttu ka silmatorkavalt ebaefektiivne, algarve saab leida märksa väiksema hulga arvutustega. Kuna efektiivsemad algoritmid on ka keerukamad, pole nende uurimine siinkohal põhjendatud, näite eesmärk on illustreerida alamprogrammide kasutamist.
2: Pascalis vormistatakse deklaratsioonid forward-lause abil; QBasicu keskkonnas varjab keskkond need programmeerija eest ära; C's ja C++'is nimetatakse neid prototüüpideks (ingl prototype); Javas pole neid üldse.
3: Kui muutujate väärtused programmeerija selja taga iseenesest muutuma hakkavad, ei kehti enam ka algoritmide õigsuse tõestused!
4: Mõnes keeles on ka dünaamiliste muutujate hävitamine automaatne --- süsteem hävitab ise need muutujad, mille väärtust ei ole enam võimalik kasutada. Seda nimetatakse prahikoristusega (ingl garbage collection) mäluhalduseks.
5: Õppematerjalile lisatud näiteprogrammid kasutavad ainult automaatseid lokaalseid muutujaid.
6: Kuigi selline parameetrite sidumise viis (kohtomistus) on levinuim, kasutatakse vahel ka muid skeeme. Näiteks nimiomistuse korral näidatakse alamprogrammi väljakutses iga tegeliku parameetri juures ka sellele vastava formaalse parameetri nimi. Käesoleva õppematerjali lisades esinevad keeled kasutavad kohtomistust.
7: Kuigi sellest üldhariduskooli matemaatikatunnis ei räägita, on ka matemaatikas funktsioonidel ja nende parameetritel tüübid. Näiteks täisosa arvutamise funktsioon ëû teisendab reaalarve täisarvudeks, mida matemaatikud tähistavad ``ëû : R ® Z'' ja loevad ``täisosa on funktsioon reaalarvude hulgast täisarvude hulka''.
8: Käesoleva õppematerjali lisades kasutatud keeled üldiselt ei toeta ei nimiparameetreid ega laiska väärtustamist. Mingil määral saab neid teiste vahenditega imiteerida, aga see on tehniliselt üsna keeruline, seetõttu me neid võtteid siinkohal ei käsitle.
9: Peaaegu kõigis programmeerimiskeskkondades on võimalik programmi töö ajal magasini seisu vaadata. Rekursiivsete programmide silumisel on see väga vajalik vahend, seega tasub enne rekursiooni puudutavate koduste ülesannete lahendama hakkamist kindlasti välja uurida, kuidas teie kasutatavas süsteemis magasinile ligi pääseb.