Peatükk 5 Algoritmide keerukus

Käesolevas peatükis tutvume algoritmi keerukuse mõistega ja vaatleme põhilisi meetodeid algoritmide keerukuse hindamiseks.

5.1 Algoritmi keerukuse mõiste

Algoritmi õigsuse kõrval on tähtis ka selle efektiivsus --- võib juhtuda, et algoritm on küll teoreetiliselt korrektne, aga praktikas ei jätku meil selle alusel koostatud programmi täitmiseks ressursse.

Algoritmi efektiivsust võib hinnata mitme erineva ressursi kasutamise seisukohalt. Kõige levinum on algoritmi alusel koostatud programmi tööaja hindamine --- seda tüüpi analüüsi nimetatakse algoritmi ajalise keerukuse (ingl time complexity) uurimiseks. Sageli on vaja hinnata ka programmi tööks kasutatava mälu mahtu --- seda nimetatakse algoritmi mahulise keerukuse (ingl space complexity) uurimiseks. Muude ressursside hindamise vajadust tuleb praktikas oluliselt harvem ette.

Esmapilgul võib tunduda, et analüüsi asemel võib teha lihtsa katse --- kirjutame programmi, paneme selle käima ja mõõdame meid huvitava ressursi kulu vahetult. Siiski pole selline lahendus alati kasutatav.

Esiteks võib juhtuda, et ülesanne on nii suur ja keeruline, et otsene mõõtmine pole praktiliselt võimalik --- näiteks võib mõne ülesande lahendamine ebaefektiivse algoritmiga isegi parimatel superarvutitel võtta sajandeid. On selge, et nii kaua lahendust oodata ei saa. Sageli ongi algoritmi keerukuse analüüsimise eesmärgiks hinnata, kas ülesanne on olemasolevate ressurssidega lahendatav.

Teiseks võib algoritmi tööaeg erinevate algandmete korral olla erinev, mis tähendab, et ühest katsest ei piisa, neid tuleks teha mitmeid. Ja selleks, et otsustada, kui palju ja milliste andmetega katseid teha, on ikkagi vaja mingit eelnevat teoreetilist tööd.

Selleks, et arvestada algoritmi tööaja (või muu ressursikulu) sõltuvust algandmetest, väljendatakse algandmete ``raskusaste'' mingi arvulise suurusena ja avaldatakse tööaja hinnang funktsioonina, mille parameetriks on see algandmete raskusaste.

Analüüsi lihtsustamiseks püütakse andmete raskust väljendada võimalikult väikese arvu parameetrite abil. Kõige sagedamini kasutatakse parameetrina just algandmete mahtu: faili töötlemise algoritmi puhul faili suurust, arvujada töötlemisel selle elementide arvu jne.

Näiteks arvujadast maksimaalse väärtuse leidmiseks tuleb üldjuhul jada elemendid kõik ükshaaval läbi vaadata. Kui me loeme algoritmi sammuks jada ühe elemendi uurimise, siis kulutab selline järjestikune läbivaatus n-elemendilise jada töötlemiseks täpselt n sammu.

Sageli toob algandmete raskusastme lihtsustamine üheks parameetriks kaasa mõningase ebatäpsuse.

Näiteks selleks, et kontrollida, kas antud arv antud n-elemendilises jadas esineb või mitte, tuleb halvimal juhul läbi vaadata kõik n elementi --- enne ei saa me kindlalt väita, et otsitavat nende hulgas pole. Seevastu parimal juhul on otsitav element jadas esimene ja me saame vaid ühe võrdluse järel kinnitada, et see arv jadas esineb. Edaspidises näeme, et keskmiselt kulub n-elemendilises jadas esineva elemendi leidmiseks n / 2 võrdlust.

Jadast väärtuse leidmine pole selles mõttes erandlik ülesanne. Paljude algoritmide puhul on võimalik rääkida eraldi nende keerukusest halvimal juhul (ingl worst-case complexity), parimal juhul (ingl best-case) või keskmiselt (ingl average-case).

Lauaarvuti rakendusprogrammides huvitab meid tavaliselt keskmine keerukus. Näiteks otsimisprogrammi kasutaja jaoks on üldjuhul piisav teada, et programm suudab sekundis läbi vaadata keskmiselt 500 kB andmeid ja pole kuigi oluline, kas programm kulutab faili esimeses pooles iga kilobaidi läbivaatamiseks 1 ms ja teises pooles 3 ms või vastupidi.

Hoopis teine on lugu nn sardsüsteemide puhul, kus arvuti juhib mingit reaalajas töötavat seadet. Näiteks auto pidureid juhtiva pardaarvuti puhul on kindlasti oluline just selle reaktsiooniaeg halvimal juhul. Vaevalt lepib pidurisüsteemi viivituse tõttu haiglasse sattunud sõitja tehase lohutusega, et keskmiselt reageerivad pidurid piisavalt kiiresti ja teised sama marki auto omanikud pole veel avariid teinud.

5.1.1 Asümptootiline keerukus

Sageli on ühe ülesande lahendamiseks võimalik kasutada mitut erinevat algoritmi. Tavaliselt on programmi kasutajad sellisel juhul huvitatud võimalikult efektiivsest lahendusest. Algoritmide keerukuse analüüsi üks oluline rakendus ongi erinevate algoritmide keerukuse võrdlemine.

Kuna programmide ressursivajadused on enamasti suuremad just suuremahuliste andmete töötlemisel, on ka algoritmide efektiivsuse analüüsimisel loomulik pöörata tähelepanu põhiliselt sellele juhule.

Algoritmi sellist uurimist nimetatakse asümptootilise keerukuse (ingl asymptotic complexity) hindamiseks ja seda tüüpi analüüsis keskendutakse just algoritmi keerukusfunktsiooni kasvukiiruse (ingl growth) uurimisele.

Algoritmi keerukusfunktsiooni kasvukiirus näitab, kui kiiresti kasvab selle algoritmi alusel koostatud programmi ressursivajadus töödeldavate andmete mahu kasvades.

Veidi lihtsustades võib eeldada, et kui mingi algoritmi ajaline keerukus on f(n), siis selle alusel koostatud programmi tööaeg avaldub kujul c f(n), kus c on kasutatava arvuti kiirust iseloomustav konstant. Kui c on ühe arvuti piires muutumatu konstant, siis võime algoritmide efektiivsuse võrdlemisel piirduda ainult f(n) uurimisega.

Tabelist 5.1 on näha, et sisendandmete mahu suurenemisel võib programmi tööaja kasv, sõltuvalt kasutatava algoritmi keerukusest, olla väga erinev. Seejuures sõltub kasv algoritmi keerukust iseloomustavast funktsioonist f(n), kuid ei sõltu arvutit iseloomustavast konstandist c. Samast on näha ka, et programmi tööaja kasv on lausa plahvatuslik, kui algoritmi keerukus avaldub eksponentfunktsioonina.¹

Funktsioon c f(n) Suhe f(25) / f(5)

c₁ 1

c₂ logn 2

c₃ n 5

c₄ n logn 10

c₅ n² 25

c₆ n³ 125

c₇ 2ⁿ 1 048 576

c₈ 3ⁿ 3 486 784 401

Table 5.1: Programmi tööaja kasv andmete mahu kasvades

Polünoomide² ja eksponentfunktsioonide kasvu põhimõttelist erinevust illustreerib veel paremini tabel 5.2. Selle tabeli esimeses veerus on programmi ajalise keerukuse hinnang, kolmes järgmises veerus programmi poolt sekundis töödeldavate andmete maht vastavalt 1, 10 ja 100 MOPS (miljonit operatsiooni sekundis) jõudlusega arvutil ja viimases veerus töödeldavate andmete mahu kasv arvuti jõudluse 10-kordsel kasvul.

Keerukus 1 MOPS 10 MOPS 100 MOPS Vahe

n 1 000 000 10 000 000 100 000 000 10 korda

n² 1 000 ~ 3 162 10 000 ~ 3 korda

n³ 100 ~ 215 ~ 464 ~ 2 korda

2ⁿ ~ 20 ~ 23 ~ 26 ~ 3 võrra

3ⁿ ~ 13 ~ 15 ~ 17 ~ 2 võrra

Table 5.2: Töödeldavate andmete mahu kasv arvuti kiiruse kasvades

Tabelist on näha, et kui algoritmi keerukusfunktsioon on polünoom, siis arvuti jõudluse kasvamisel kordades kasvab kordades ka töödeldavate andmete maht. Kui aga algoritmi keerukus avaldub eksponentfunktsioonina, kasvab töödeldavate andmete maht ainult mingi konstandi võrra.

5.1.2 Funktsioonide kasv

Nagu eelpool märgitud, avaldub algoritmi keerukus algandmete raskusastme funktsioonina. Seega on meil algoritmide keerukuse võrdlemiseks vaja osata võrrelda funktsioone.

Osutub, et see polegi nii lihtne. Vaatleme näiteks joonist 5.1. Kui me võrdleme f(n) ja g(n) väärtusi kohal n₀, saame tulemuseks f(n₀) < g(n₀); kohal n₁ saame f(n₁) = g(n₁); kohal n₂ aga hoopis f(n₂) > g(n₂).

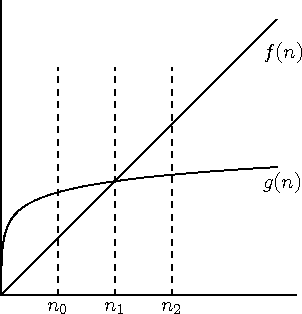
Joonis 5.1: Funktsioonide võrdlemine

Selle ``vastuolu'' põhjus on muidugi asjaolus, et funktsioonide väärtused sõltuvad nende argumentide väärtustest³ ja selle lahendamiseks on leitud mitmesuguseid funktsioonide võrdlemise viise. Algoritmide analüüsimisel on neist kõige kasulikumaks osutunud funktsioonide võrdlemine nende kasvukiiruse järgi.

Öeldakse, et funktsiooni f(n) kasvukiirus ei ületa funktsiooni g(n) kasvukiirust, ja kirjutatakse f(n) = O(g(n)), kui leiduvad positiivsed arvud c₁ ja n₀, mille korral kehtib

" n ³ n₀ : f(n) £ c₁ g(n).

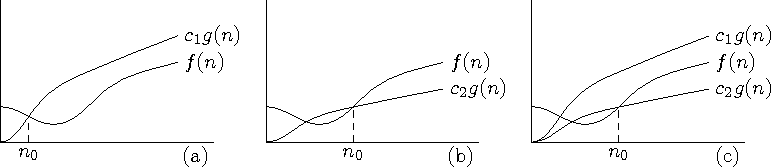
Joonis 5.2: (a) f(n) = O(g(n)); (b) f(n) = W(g(n)); (c) f(n) = Q(g(n))

Paneme tähele, et f(n) = O(g(n)) definitsioon ei piira mitte f(n) või g(n) väärtusi endid, vaid nende väärtuste suhet f(n) / g(n), mis ei tohi lõpmatult kasvada.

Kuna konstant c₁ piirab suhet f(n) / g(n) ``ülalt'', võib funktsioonide kasvule O-hinnanguid anda suvalise ``liiaga'' --- g(n) võib kasvada kuitahes palju kiiremini kui f(n).

Näiteks f(n) = 3 n² + 1 korral kehtivad nii f(n) = O(n²) kui ka f(n) = O(n³), f(n) = O(n⁴) ja isegi f(n) = O(2ⁿ). Nende kõigi puhul on O definitsiooni tingimused rahuldatud, kui valime c₁ = 4 ja n₀ = 1.

Küll aga ei kehti f(n) = O(n) (ehk teisiti öeldes, kehtib f(n) ¹ O(n)), sest pole võimalik valida O definitsiooni nõudeid rahuldavaid c₁ ja n₀. Tõepoolest, mistahes c₁ korral f(n) > c₁ n, kui n ³ c₁/3, seega pole ühegi c₁ jaoks võimalik leida O definitsioonis nõutud konstanti n₀.

Veel kirjutatakse f(n) = W(g(n)), kui leiduvad positiivsed c₂ ja n₀, mille korral kehtib

" n ³ n₀ : f(n) ³ c₂ g(n).

Väited f(n) = W(g(n)) ja g(n) = O(f(n)) on samaväärsed. Tõepoolest, oletame, et f(n) = W(g(n)). Vastavalt W definitsioonile peavad leiduma sellised positiivsed n₀ ja c₂, et iga n ³ n₀ korral kehtib f(n) ³ c₂ g(n). Kui nüüd võtame c₁ = 1 / c₂, siis peab iga n ³ n₀ korral kehtima ka g(n) £ c₁ f(n). See aga on täpselt g(n) = O(f(n)) definitsioonis nõutud tingimus. Vastupidise järelduse võime tõestada analoogiliselt.

Veel kirjutatakse f(n) = Q(g(n)), kui leiduvad positiivsed c₁, c₂ ja n₀, mille korral kehtib

" n > n₀ : c₂ g(n) £ f(n) £ c₁ g(n).

Jällegi on lihtne veenduda, et f(n) = Q(g(n)) parajasti siis, kui f(n) = O(g(n)) ja f(n) = W(g(n)).

Erinevalt seosest O piirab seose Q definitsioon funktsioonide f(n) ja g(n) väärtuste suhet mitte ainult ``ülalt'', vaid ka ``alt''. Seega f(n) = Q(g(n)) tähendab, et f(n) ei kasva küll kiiremini kui g(n), kuid samal ajal ei jää kasvus ka oluliselt maha.

Ülaltoodud näites vaadeldud f(n) = 3 n² + 1 korral f(n) = Q(n²), kuid f(n) ¹ Q(n³), f(n) ¹ Q(n⁴) ja f(n) ¹ Q(2ⁿ). Väite f(n) = Q(n²) kehtivuses veendumiseks valime c₁ = 4, c₂ = 3 ja n₀ = 1. Ülejäänud juhtudel on mistahes positiivse c₂ korral võimalik näidata, et n piisavalt suurte väärtuste juures jäävad f(n) väärtused teistega võrreldes liiga väikesteks.

Avaldisi f(n) = W(g(n)) ja f(n) = Q(g(n)) loetakse vastavalt ``eff-enn on oomega-gee-enn'' ja ``eff-enn on teeta-gee-enn''. Avaldist f(n) = O(g(n)) loetakse ``eff-enn on oo-gee-enn'', kuigi rangelt võttes peaks selles avaldises võrdusmärgist paremal olema kreeka täht omikron.

Edasises kasutame mõnikord seoseid O, W ja Q ka mitme muutuja funktsioonidel. Need üldistused defineeritakse loomulikul viisil: näiteks f(n, m) = O(g(n, m)), kui leiduvad c₁, n₀ ja m₀, mille korral kehtib

" n ³ n₀, m > m₀ : f(n, m) £ c₁ g(n, m).

5.1.3 Kasvuseoste omadused

Nagu eelnevatest lõikudest näha, võib tõmmata paralleele funktsioonide vahel kehtivate seoste O, W ja Q ning arvude vahel kehtivate seoste £, ³ ja = vahele. See ei tohiks olla eriline üllatus, sest funktsioonide kasvu asusimegi uurima just eesmärgiga leida vahend nende võrdlemiseks.

Siiski pole kõik arvude võrdlemise seoste omadused funktsioonidele üle kantavad. Nimelt tekitavad funktsioonide kasvukiiruste võrdlemise seosed funktsioonide vahel osalise järjestuse (ingl partial order), kuid arvude võrdlemise seosed arvude vahel lineaarse järjestuse (ingl total order).

Nende erinevus seisneb selles, et mistahes kaks arvu on alati võrreldavad --- suvaliste arvude a ja b puhul kehtib alati vähemalt üks väidetest a £ b või a ³ b ---, aga kahe funktsiooni f(n) ja g(n) puhul ei tarvitse kehtida ei f(n) = O(g(n)) ega f(n) = W(g(n)). Üks võrreldamatute kasvukiirustega funktsioonide paar on näiteks f(n) = n ja g(n) = n^{1 + sinn}.

Algoritmide keerukuse analüüsimisel on sageli kasu seoste O, W ja Q järgmistest omadustest:

" c > 0 : c f(n) = Q(f(n))
see tähendab, et funktsiooni korrutamine konstandiga ei muuda selle kasvukiirust; erijuhul c = 1 saame f(n) = Q(f(n)), järelikult on seos Q refleksiivne, täpselt nagu seos = arvudel; samast järeldub, et ka seosed O ja W on refleksiivsed, täpselt nagu seosed £ ja ³ arvudel; erijuhul f(n) = 1 saame c = Q(1), järelikult on kõigi konstantsete funktsioonide kasvukiirused võrdsed;
f(n) = O(g(n)) Ù g(n) = O(h(n)) É f(n) = O(h(n))
f(n) = W(g(n)) Ù g(n) = W(h(n)) É f(n) = W(h(n))
see tähendab, et seosed O ja W on transitiivsed, täpselt nagu seosed £ ja ³ arvudel; sellest järeldub, et ka seos Q on transitiivne, täpselt nagu seos = arvudel;
f(n) = Q(h(n)) Ù g(n) = O(h(n)) É (f(n) + g(n)) = Q(h(n))
kahe funktsiooni summa kasvu määrab kiirema kasvuga liidetav;
f₁(n) = Q(g₁(n)) Ù f₂(n) = O(g₂(n)) É (f₁(n) f₂(n)) = O(g₁(n) g₂(n))
f₁(n) = Q(g₁(n)) Ù f₂(n) = W(g₂(n)) É (f₁(n) f₂(n)) = W(g₁(n) g₂(n))
seda omadust võib tõlgendada nii, et kahe funktsiooni korrutise kasv on tegurite kasvude korrutis;
kui p(n) on k. astme polünoom, siis p(n) = Q(n^k)
see tähendab, et polünoomi kasvu määrab selle kõrgeima astmega liige; väga kasulik omadus, mille põhjal võime mistahes polünoomi uurimise asendada üksliikme uurimisega;
" 0 £ r £ s : n^r = O(n^s)
see tähendab, et madalama astmega astmefunktsioon ei kasva kiiremini kõrgema astmega astmefunktsioonist; kehtib ka tugevam väide: madalama astmega funktsioon kasvab alati rangelt aeglasemalt;
" k ³ 0, b > 1 : n^k = O(bⁿ)
see tähendab, et mitte ükski astmefunktsioon ei kasva kiiremini ühestki eksponentfunktsioonist; tegelikult kasvab astmefunktsioon alati rangelt aeglasemalt;
" k > 0, b > 1 : log_b n = O(n^k)
see tähendab, et ükski logaritmfunktsioon ei kasva kiiremini ühestki astmefunktsioonist; tegelikult kasvab logaritmfunktsioon alati rangelt aeglasemalt;
" b₁ > 1, b₂ > 1 : log_b₁ n = Q(log_b₂ n)
see tähendab, et kõik logaritmfunktsioonid kasvavad sama kiirusega;
" r ³ 0 : å_{i = 1}ⁿ i^r = Q(n^{r + 1})
see tähendab, et r. järku astmerea summa kasvab nagu (r+1). astme polünoom.

Vaatleme näiteks funktsioone f(n) = (n² - n) / 2 ja g(n) = 6 n ning uurime nende kasvukiirusi. Selliste lihtsate funktsioonide puhul pole muidugi raske vahetult tuletada, et f(n) > c g(n), kui n > 12 c - 1 ja sellest järeldada, et f(n) ¹ O(g(n)), f(n) = W(g(n)) ja f(n) ¹ Q(g(n)).

Pannes tähele, et f(n) = (n² - n) / 2 = 0,5 n² - 0,5 n on 2. astme polünoom, saame omaduse 5 põhjal f(n) = Q(n²). Kuna g(n) on ilmselt 1. astme polünoom, kehtib sama omaduse põhjal g(n) = Q(n). Edasi saamegi omaduse 6 alusel f(n) ¹ O(g(n)), f(n) = W(g(n)) ja f(n) ¹ Q(g(n)), mis muidugi ei erine eelmises lõigus otseselt saadud tulemustest.

Erinevalt eelmise näite lihtsatest funktsioonidest oleks f(n) = n sqrt(n) ja g(n) = n + logn kasvukiiruste võrdlemine otseselt seoste O, W ja Q definitsioonide põhjal üsna tülikas. Neid funktsioone on oluliselt mugavam võrrelda seoste O, W ja Q eeltoodud omadusi kasutades.

Tõepoolest, elementaaralgebrast on teada, et f(n) = n sqrt(n) = n^1,5 ning omaduste 8 ja 3 põhjal saame g(n) = n + logn = O(n). Edasi on omaduse 6 nõrgema väite põhjal näha, et g(n) = O(f(n)) ehk f(n) = W(g(n)); sama omaduse tugevama väite põhjal saame f(n) ¹ O(g(n)), millest omakorda järeldub f(n) ¹ Q(g(n)).

Avaldiste teisendamisel kirjutatakse sageli näiteks f(n) = n + logn = Q(n) + O(n) = Q(n). Selle (rangelt võttes veidi ebakorrektse) kirjutise tähendus on, et f(n) koosneb kahest liidetavast, milles üks kasvab täpselt sama kiiresti kui n ja teine mitte kiiremini kui n, seega peab ka summa kasvama täpselt sama kiiresti kui n.

Ebakorrektsus seisneb selles, et O(n) pole konkreetne funktsioon, mida oleks võimalik mõne teise funktsiooniga liita. Siiski on selline notatsioon just mugavuse tõttu laialt levinud. Tuleb ainult olla ettevaatlik, et mitte teha ebaõigeid teisendusi. Näiteks ``taandamine'' f(n) = logn / loglogn = O(n) / O(n) = O(1) on ebaõige, sest kuigi logn ja loglogn on mõlemad O(n), pole nende kasvukiirused sugugi võrdsed --- nad ainult kasvavad mõlemad aeglasemalt kui n.

5.2 Algoritmide keerukuse hindamine

Järgnevates lõikudes vaatleme tähtsamaid võtteid algoritmide ajalise keerukuse hindamiseks. Kuna just juhtkonstruktsioonid määravad, milliseid primitiive ja kui palju kordi täidetakse, ei tohiks olla eriline üllatus, et nii algoritmi ajaline keerukus kui ka selle hindamise võtted on otseselt seotud algoritmi struktuuriga.

Mahulise keerukusega tegeleme järgmistes peatükkides andmestruktuure vaadeldes, sest programmi mäluvajadus sõltub otseselt just andmete, mitte algoritmi struktuurist.

5.2.1 Maksumuse mudel

Selleks, et hinnata algoritmi kõigi primitiivide täitmiseks kuluvat koguaega, on muidugi vaja teada iga primitiivi täitmiseks kuluvat aega. Seda infot kõigi primitiivide kohta kokku nimetatakse süsteemi maksumuse mudeliks (ingl cost model). Erinevate operatsioonide maksumused võivad sõltuda nii arvuti riistvarast, operatsioonisüsteemist kui ka kasutatavatest programmeerimisvahenditest.

Lihtsaima mudeli puhul eeldame, et kõigi primitiivide maksumused on võrdsed. Sellisel juhul saame algoritmi ajaliseks keerukuseks primitiivi maksumuse ja täidetud primitiivide arvu korrutise. Kuigi selline mudel pole peaaegu kunagi päris täpne, on see sageli siiski piisav.

Näiteks võime arvutusalgoritmide hindamisel võrdsustada kõik aritmeetilised tehted kõigi standardsete arvutüüpide vahel. Kuigi tehte sooritamiseks kuluv aeg sõltub tavaliselt nii sooritatavast tehtest kui ka operandide tüüpidest (ja veel paljudest muudest asjadest), on need erinevused suhteliselt väikesed ja, mis peamine, konstantsed. Seega, kui meid huvitab ainult tööaja kasvu sõltuvus algandmetest, pole üksikute tehete vahelistel erinevustel meie jaoks erilist tähtust.

Selline lihtne mudel pole aga piisav, kui programmeerimissüsteemi primitiivide hulgas on ka keerulisemaid operatsioone. Näiteks mingi andmehulga sorteerimine või sellest hulgast vajalike andmete leidmine on operatsioonid, mille ajakulu ei sõltu mitte ainult andmetüüpidest, vaid ka andmemahtudest. Selliseid sõltuvusi enam eirata ei või.

5.2.2 Lineaarne algoritm

Algoritmi, milles ainsa juhtkonstruktsioonina on kasutusel järjend, nimetatakse lineaarseks (ingl linear). Kuna sellises algoritmis täidetakse iga primitiivi täpselt üks kord, on terve algoritmi täitmiseks kuluv aeg primitiivide täitmisaegade summa.

Täpsemalt, kui algoritm on kujul

käsk-1
käsk-2
...
käsk-k

ning käsk-i täitmiseks kuluv aeg on f_i(n), siis avaldub algoritmi täitmise koguaeg T(n) kujul

T(n) = f₁(n) + f₂(n) + ... + f_k(n).

Erijuhul, kui kõigi primitiivide täitmisajad on konstandid, on seda ilmselt ka terve lineaarse algoritmi täitmise aeg.

Kui primitiivide täitmise ajad on keerukamad funktsioonid, võib kasvukiiruse avaldise lihtsustamiseks kasutada lõigus 5.1.3 vaadeldud omadusi.

5.2.3 Hargnemistega algoritm

Algoritmi, milles juhtkonstruktsioonidena on kasutusel järjend ja valik, nimetatakse hargnemistega (ingl branching) algoritmiks. Sellises algoritmis täidetakse iga primitiivi ülimalt üks kord, seega ei saa algoritmi täitmiseks kuluv aeg mingil juhul ületada kõigi primitiivide täitmisaegade summat, küll aga võib olla sellest väiksem.

Täpsemalt, kui algoritm on kujul

kui tingimus
tõene-käsud
muidu
väär-käsud
lõppkui

ning tõene-käsud ajaline keerukus on f₁(n), väär-käsud ajaline keerukus f₂(n) ja tingimuse tõeväärtuse arvutamise keerukus f₀(n), siis terve algoritmi ajaline keerukus on parimal juhul

T_min(n) = f₀(n) + min(f₁(n), f₂(n))

ja halvimal juhul

T_max(n) = f₀(n) + max(f₁(n), f₂(n)).

Kui tingimus kehtib tõenäosusega p⁴, on algoritmi keskmine keerukus

T(n) = f₀(n) + p f₁(n) + (1 - p) f₂(n).

Selle valemi põhjenduseks paneme tähele, et igal juhul tuleb väärtustada tingimus, kulutades selleks f₀(n). Edasi tuleb tõenäosusega p täita tõene-käsud, kulutades selleks f₁(n), või tõenäosusega 1 - p täita väär-käsud, kulutades selleks f₂(n). Kui me käivitame seda algoritmi M korda, siis keskmiselt p M juhul on tingimus tõene, ülejäänud M - p M = (1 - p) M juhul aga on tingimus väär. Kokku kulutame algoritmi M-kordsel käivitamisel M f₀(n) + p M f₁(n) + (1 - p) M f₂(n), mis annabki ühe käivitamiskorra keskmiseks hinnaks f₀(n) + p f₁(n) + (1 - p) f₂(n).

Vaatleme näiteks ühest valikulausest koosnevat algoritmi:

--- n, k Î N; n ³ k > 0
kui n / k Î N
--- midagi, mis on Q(n)
muidu
--- midagi, mis on Q(1)
lõppkui

Kui n ja k on programmeerimissüsteemi standardsed täisarvud, võime eeldada, et nende jaguvus on kontrollitav konstantse ajaga. Seega on selle algoritmi ajalise keerukuse hinnangud vastavalt eelpool toodud seostele

parimal juhul:
T_min(N) = Q(1) + min(Q(n), Q(1)) = Q(1) + Q(1) = Q(1);
halvimal juhul:
T_max(n) = Q(1) + max(Q(n), Q(1)) = Q(1) + Q(n) = Q(n);
keskmiselt:
kui arvudele n ja k pole seatud muid piiranguid, on jaguvuse tõenäosus 1 / k, mis annab keskmiseks ajakuluks
T(n) = Q(1) + (1 / k) Q(n) + (1 - 1 / k) Q(1) = Q(n / k),
sest pole raske näha, et n ³ k korral on T(n) avaldises domineeriv keskmine liidetav.

5.2.4 Iteratiivne algoritm

Algoritmi, milles juhtkonstruktsioonina on kasutusel kordus, nimetatakse iteratiivseks (ingl iterative). Sellises algoritmis täidetakse korduslause kehas olevaid primitiive korduvalt, seega võib selle keerukus olla üsna suur.

Kui iteratiivne algoritm on kujul

korda i¬1 ... k
käsud
lõppkorda

ning käsud ajaline keerukus on f(n), siis on kogu korduslause ajaline keerukus muidugi k f(n).

Vaatleme näiteks juba tuttavat algoritmi arvujada liikmete summa leidmiseks:

--- a_{1 ... n} --- summeeritav jada
s¬0
korda i¬1 ... n
s¬s + a_i
lõppkorda
väljasta s

Korduse kehaks on siin üks liitmis- ja üks omistamistehe, mille täitmiseks kulub ilmselt konstantne hulk aega, seega antud juhul f(n) = Q(1). Seda korduse keha täidetakse täpselt n korda, seega on korduse keerukuseks n Q(1). Lisaks sellele täidetakse enne kordust veel üks omistamine (keerukus Q(1)) ja pärast seda üks väljastamine (jälle Q(1)). Seega on algoritmi kogukeerukus

T(n) = Q(1) + n Q(1) + Q(1) = Q(1) + Q(n) + Q(1) = Q(n).

Ülesanne muutub raskemaks, kui korduse keha täitmise hind pole korduse kõigil läbimistel sama. Sellisel juhul peame käsud keerukuse avaldama kahe muutuja funktsioonina f(n, i) ja kogu korduslause ajaline keerukus avaldub summana

T(n) =

i = 1

f(n, i) = f(n, 1) + f(n, 2) + ... + f(n, k).

Väliselt on summa sarnane eelpool vaadeldud lineaarse algoritmi keerukuse avaldisega, kuid sellest ei tohi ennast petta lasta. Oluline erinevus võrreldes lineaarse algoritmiga seisneb asjaolus, et lineaarses algoritmis on summas esinevate liidetavate arv määratud programmi struktuuriga, kordusega algoritmis aga võib sõltuda sisendandmetest.

Vaatleme näiteks kahest pesastatud kordusest koosnevat algoritmi, mis loendab antud arvujadas kõik inversioonid (paarid, kus suurem arv on jadas väiksemast eespool):

--- a_{1 ... n} --- uuritav jada
k¬0
korda i¬1 ... n
    korda j¬i + 1 ... n
       kui a_i > a_j
          k¬k + 1
       lõppkui
    lõppkorda
lõppkorda
väljasta k

Selliste pesastatud juhtkonstruktsioonidega algoritmide keerukust on sageli lihtsam arvutada, liikudes algoritmi struktuuris seestpoolt väljapoole.

Valikulauses on nii arvude võrdlemine kui ka tingimuslikult täidetav omistamine konstantse ajaga operatsioonid, seega on kogu valikulause ajaline keerukus Q(1).

Valikulause ise on sisemise korduslause keha, teda täidetakse j väärtustel i + 1 kuni n, see tähendab täpselt n - i korda. Kuna selle korduse keha täitmise maksumus on kõigil läbimistel sama, on meil tegemist lihtsama juhuga ja korduse kogukeerukus f(n, i) = (n - i) Q(1).

Sisemine korduslause omakorda on välimise korduse keha, teda täidetakse i väärtustel 1 kuni n. Kuna selle korduse keha täitmise maksumus on erinevatel läbimistel erinev, on meil seekord tegemist keerukama juhuga ja korduse kogukeerukus

T(n)

(n - 1) Q(1) + (n - 2) Q(1) + ... + (n - n) Q(1)

((n - 1) + (n - 2) + ... + (n - n)) Q(1)

n(n - 1)

Q(1) = Q(n²) Q(1) = Q(n²).

Toodud näites on üleminek teiselt realt kolmandale tehtud aritmeetilise jada summa valemi põhjal. Kahjuks pole selliste summade lihtsustamiseks üldist eeskirja --- neisse tuleb suhtuda loominguliselt.

Muidugi tasub võimalusel alati kasutada seoste O ja Q lõigus 5.1.3 vaadeldud omadusi, korduslausete puhul on sageli abiks just omadus 10.

Osutub, et ka käesoleval juhul saaks me kasutada just seda omadust: T(n) avaldises

T(n) = ((n - 1) + (n - 2) + ... + (n - n)) Q(1)

võime sulgudes olevat summat S teisendada järgmiselt:

(n - 1) + (n - 2) + ... + (n - n)

0 + 1 + ... + (n - 1)

0 +

i = 1

i - n

Q(1) + Q(n²) - Q(n) = Q(n²).

Veel võib olla kasulik meeles pidada, et O-hinnanguid võib, erinevalt Q-hinnanguist, anda suvalise liiaga. See tähendab, et kui korduse keerukuse täpse avaldise lihtsustamine ei õnnestu, võime Q-hinnangu asemel anda mõningase liiaga O-hinnangu, ``ümardades'' kõik liidetavad ülespoole mingiks lihtsustamiseks soodsama kujuga avaldiseks.

Näiteks inversioonide loendamise programmi keerukuse avaldise lihtsustamisel võime kasutada ära asjaolu, et kõigis liidetavates on esimene korrutis n-st väiksem arv, seega saame

T(n)	=	(n - 1) Q(1) + (n - 2) Q(1) + ... + (n - n) Q(1)
	<	n Q(1) + n Q(1) + ... + n Q(1)
	=	n² Q(1) = Q(n²)
T(n)	=	O(n²).

Selle näite puhul juhtus, et ka ``ülespoole ümardatud'' hinnang on täpne, aga alati ei pruugi see nii olla. Sellepärast ei või me liiaga antud hinnangu avaldamisel enam kasutada seost Q.

5.2.5 Rekursiivne algoritm

Rekursiivse alamprogrammina avaldatavat algoritmi nimetatakse samuti rekursiivseks (ingl recursive). Nagu rekursiivne alamprogramm ise defineeritakse iseenda kaudu, tehakse seda ka tema keerukusfunktsiooniga.

Vaatleme näiteks juba varasemast tuttavat rekursiivset algoritmi antud naturaalarvu n faktoriaali leidmiseks:

--- n Î N
kui n = 0
    tagasta 1
muidu
    --- rekursioon
    tagasta n * (n - 1)!
lõppkui

Selle algoritmi tööaja hinnangu T(n) võib avaldada kujul

T(n) =

ì
í
î

Q(1),	kui n = 0,
T(n - 1) + Q(1),	kui n > 0,

kus juhul n > 0 väljendab T(n - 1) rekursiivsele väljakutsele kuluvat aega ja Q(1) selle väärtuse kasutamist n! arvutamisel.

Sellised rekurrentsed (ingl recurrent) võrrandid ja võrrandisüsteemid pole matemaatikas midagi haruldast. Kõige üldisem meetod nende lahendamiseks on: tuleb rekurrentseid pöördumisi mõned korrad avaldisse sisse asendada ja püüda vastuse üldkuju ära arvata. Tekkinud hüpoteeside tõestamiseks on tavaliselt kõige parem matemaatilise induktsiooni meetod.

Näiteks faktoriaali leidmise algoritmi puhul saame

T(n)	=	T(n - 1) + Q(1)
	=	T(n - 2) + Q(1) + Q(1)
	=	T(n - 3) + Q(1) + Q(1) + Q(1),

millest on juba küllalt lihtne pakkuda T(n) = (n + 1) Q(1) = Q(n).

Tabelis 5.3 on ära toodud mõnede rekursiivsete algoritmide analüüsimisel sageli esinevate rekurrentsete võrrandite lahendid. Tabeli vasakpoolses veerus on antud T(n) avaldis n > 0 jaoks, lisaks eeldatakse kõigil juhtudel rajatingimust T(0) = Q(1).

T(n) avaldis lahend

T(n / c₁) + Q(1) Q(logn)

T(n - 1) + Q(1) Q(n)

c₂ T(n / c₂) + Q(1) Q(n)

c₃ T(n / c₃) + Q(n) Q(n logn)

T(n - 1) + Q(n) Q(n²)

c₄ T(n - 1) + Q(1) Q(c₄ⁿ)

Table 5.3: Mõnede sageli esinevate rekurrentsete võrrandite lahendid

5.3 Praktiline nõuanne

Algoritmide efektiivsuse hindamisele pühendatud peatüki lõpetuseks tasub märkida, et efektiivsus pole siiski algoritmi kõige tähtsam omadus. Õigsus on alati efektiivsusest olulisem. Tõepoolest, millist kasu võiks loota programmist, mis töötab küll välkkiirelt, kuid annab valesid vastuseid?

Ülesanded

Ülesanne 1 Kontrollida otseselt seoste O, W ja Q definitsioonidest lähtudes, kas kehtivad väited

(a) 2ⁿ⁺¹ = O(2ⁿ);	(d) 2²ⁿ = O(2ⁿ);
(b) 2ⁿ⁺¹ = W(2ⁿ);	(e) 2²ⁿ = W(2ⁿ);
(c) 2ⁿ⁺¹ = Q(2ⁿ);	(f) 2²ⁿ = Q(2ⁿ).

Põhjendada oma vastuseid ka lõigus 5.1.3 toodud omaduste abil.

Ülesanne 2 Vaatleme järgmisi funktsioone:

sqrt(n)	n	2ⁿ	n logn
n - n³ + 7n⁵	n² + logn	n²	n³
logn	n^1/3 + logn	(logn)²	log₂ n
loglogn	(1/3)ⁿ	(3/2)ⁿ	6

Grupeerida need funktsioonid nii, et ühes grupis oleks koos sama kasvukiirusega funktsioonid. Järjestada grupid omavahel funktsioonide kasvukiiruste kasvamise järjekorras. (Kõigi nende funktsioonide kasvukiirused on omavahel võrreldavad.)

Ülesanne 3 Vaatleme järgmist algoritmi:

--- n Î N
korda i¬1 ... n
    korda j¬1 ... i
       väljasta i, j
    lõppkorda
lõppkorda

Milline on selle algoritmi ajaline keerukus parimal, halvimal ja keskmisel juhul? Kas teie antud hinnangud on täpsed või liiaga? Põhjendada oma vastuseid.

Ülesanne 4 Vaatleme algoritmi Bitte naturaalarvu kahendkujus esinevate 1-bittide loendamiseks (kus div ja mod tähendavad täisarvulise jagamise jagatist ja jääki):

--- n Î N
kui n = 0
tagasta 0
muidu
tagasta Bitte(n div 2) + (n mod 2)
lõppkui

Milline on selle algoritmi ajaline keerukus?

Kirjandus

Jüri Kiho. Algoritmid ja andmestruktuurid. Tartu Ülikool, 2003.: Andmestruktuuride realiseerimist ja klassikalisi algoritme käsitlev õpik, milles leidub ka keerukuse põhimõistetele pühendatud peatükk. 148 lk.
Valdo Praust. Keerukusteooria alused. Ülikoolide Informaatikakeskus, 1996.: Algoritmide ja ülesannete keerukuse teoreetilisemale poolele keskenduv õpik. 212 lk.
Thomas H. Cormen, Clifford Stein, Charles Leiserson, Ronald Rivest. Introduction to Algorithms. MIT, 2001.: Eelmise trükiga klassikaks saanud algoritmide ja andmestruktuuride põhiõpik, mis annab üsna hea ülevaate ka algoritmide keerukuse hindamisest ja selleks vajalikust matemaatilisest aparatuurist. 1180 lk.
Томас Кормен, Чарльз Лейзерсон, Рональд Ривест. Алгоритмы: построение и анализ. МЦНМО, 2001.: Eelmise tõlge. 960 lk.
Herbert S. Wilf. Algorithms and Complexity. Prentice Hall, 1986.: Ülikooli keskmiste kursuste tasemele orienteeritud konspekt. 240 lk.
http://www.cis.upenn.edu/~wilf/AlgComp2.html

1: Eksponentfunktsiooniks nimetatakse funktsiooni kujul a^x, kus a on konstant ja x funktsiooni argument. Mitte segi ajada astmefunktsiooniga, mis avaldub kujul x^a.
2: Astmefunktsioonid on polünoomide lihtsamad erijuhud.
3: See ju ongi funktsioonide mõte!
4: Siin ja edaspidi märgime tõenäosusi mitte protsentides, vaid reaalarvudega 0 ... 1. Arvestades, et protsent tähendab sajandikku, saame 20% = 20 / 100 = 0,2. Vahe on selles, et viimast kuju kasutades ei pea valemites tõenäosusi sajaga jagama, mis muudab valemid veidi lihtsamaks ja ülevaatlikumaks.

Funktsioon c f(n)	Suhe f(25) / f(5)
c₁	1
c₂ logn	2
c₃ n	5
c₄ n logn	10
c₅ n²	25
c₆ n³	125
c₇ 2ⁿ	1 048 576
c₈ 3ⁿ	3 486 784 401

Keerukus	1 MOPS	10 MOPS	100 MOPS	Vahe
n	1 000 000	10 000 000	100 000 000	10 korda
n²	1 000	~ 3 162	10 000	~ 3 korda
n³	100	~ 215	~ 464	~ 2 korda
2ⁿ	~ 20	~ 23	~ 26	~ 3 võrra
3ⁿ	~ 13	~ 15	~ 17	~ 2 võrra

T(n) avaldis	lahend
T(n / c₁) + Q(1)	Q(logn)
T(n - 1) + Q(1)	Q(n)
c₂ T(n / c₂) + Q(1)	Q(n)
c₃ T(n / c₃) + Q(n)	Q(n logn)
T(n - 1) + Q(n)	Q(n²)
c₄ T(n - 1) + Q(1)	Q(c₄ⁿ)