Peatükk 8 Mittelineaarsed andmestruktuurid

Käesolevas peatükis jätkame tähtsamate andmestruktuuride ja nendega seotud algoritmide uurimist. Seekord võtame vaatluse alla objektid, mille sisemine struktuur on keerulisem kui lihtsalt nende elementide loend, ja mida seetõttu nimetatakse ``mittelineaarseteks''.

8.1 Põhilised mittelineaarsed struktuurid

Tähtsaim mittelineaarne andmestruktuur on graaf. Arvutiteaduses on väga vähe ülesandeid, mis poleks ühel või teisel moel esitatavad graafiülesannetena. Graafi tähtsaim erijuht on puu. Nende kahega järgnevalt tutvumegi.

8.1.1 Graaf

Graaf (ingl graph) on matemaatiline objekt, mis koosneb mingist hulgast tippudest (ingl vertex) ja neid tippe paarikaupa ühendavatest servadest (ingl edge). Asjaolu, et graafi G tippude hulk on V ja servade hulk E, märgitakse tavaliselt G = (V, E).

Kui graafi tippe u ja v ühendaval serval ei ole suunda määratud (seda serva pidi võib liikuda nii tipust u tippu v kui ka vastupidi), siis nimetatakse seda orienteerimata ehk suunamata servaks ehk lühemalt lihtsalt servaks ja tähistatakse e = {u, v}.

Kui aga serval on suund määratud, nimetatakse seda orienteeritud ehk suunatud servaks ehk kaareks (ingl arc) ja tähistatakse e = (u, v).

Joonisel kujutatakse graafi tippe tavaliselt punktide, sõõride või kastikestena. Suunamata servi kujutatakse vastavaid tippe ühendavate joontena ja suunatud servi nooltena.

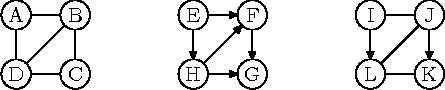
Joonis 8.1: Graafide näiteid

Graafi, mille kõik servad on suunamata, nimetatakse suunamata graafiks (ingl undirected graph) ehk lühemalt lihtsalt graafiks. Graafi, mille kõik servad on suunatud, nimetatakse suunatud graafiks (ingl directed graph). Graafi, mille osa servi on suunatud ja osa suunamata, nimetatakse segagraafiks. Näiteks joonisel 8.1 toodud graafidest on vasakpoolne suunamata, keskmine suunatud ja parempoolne segagraaf.

Teeks (ingl path) graafis G = (V, E) nimetatakse ``järjestikuste'' servade jada e₁ = {v₀, v₁}, e₂ = {v₁, v₂}, ..., e_n = {v_n-1, v_n}, milles iga serva lõpptipp on talle järgneva serva algustipp.

Ahelaks (ingl chain) nimetatakse teed, mis ei läbi ühtki serva korduvalt ja lihtahelaks (ingl simple chain) ahelat, mis ei läbi korduvalt ühtki tippu. Tsükliks (ingl cycle) nimetatakse ahelat ja lihttsükliks (ingl simple cycle) lihtahelat, mille algus- ja lõpptipp langevad kokku (v₀ = v_n). Silmuseks (ingl loop) nimetatakse ühest servast koosnevat tsüklit.¹

Graafi G = (V, E) alamgraafiks (ingl subgraph) nimetatakse mistahes graafi G' = (V', E'), mille korral kehtib V' Í V ja E' Í E. See tähendab, et alamgraaf on saadav ülemgraafist mingi hulga tippude ja servade eemaldamise teel. Asjaolu, et G' on G alamgraaf, tähistatakse G' Í G.

Graafi G alamgraafi G', mis ei ole võrdne graafi G endaga, nimetatakse tema pärisalamgraafiks (ingl proper subgraph) ja seda tähistatakse G' Ì G.

Tähtsal kohal on graafiteoorias sidususe mõiste. Suunamata graafi nimetatakse sidusaks (ingl connected), kui selle mistahes tipupaari v₁, v₂ jaoks leidub tee tipust v₁ tippu v₂.

Graafi G alamgraafi G' nimetatakse graafi G sidususkomponendiks (ingl connected component), kui G' on sidus ja graafis G ei leidu sidusat alamgraafi G'', mis sisaldaks graafi G' pärisalamgraafina. See tähendab, et sidususkomponent on maksimaalne sidus alamgraaf, seda ei saa kasvatada talle uute servade või tippude lisamisega ilma sidusust rikkumata.

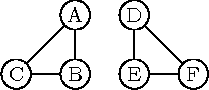
Joonis 8.2: Suunamata graafi sidususkomponendid

Näiteks joonisel 8.2 toodud graafis on kaks sidususkomponenti: tipud A, B, C ja kõik nendega seotud servad ning tipud D, E, F ja kõik nendega seotud servad.

Suunatud või segagraafi G nimetatakse sidusaks, kui graafi G kõigi kaarte (v₁, v₂) suunamata servadega {v₁, v₂} asendamisel saadud suunamata graaf G' on sidus, ja tugevalt sidusaks (ingl strongly connected), kui G mistahes tipupaari v₁ ja v₂ jaoks leidub nii tee tipust v₁ tippu v₂ kui ka tee tipust v₂ tippu v₁. Analoogiliselt võime eristada ka sidususkomponente ja tugevalt sidusaid komponente (ingl strongly connected component).²

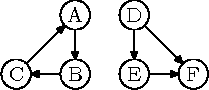
Joonis 8.3: Suunatud graafi sidususkomponendid

Näiteks joonisel 8.3 toodud suunatud graafis on kaks sidususkomponenti: tipud A, B, C ja kõik nendega seotud kaared ning tipud D, E, F ja kõik nendega seotud kaared. (Kaarte asendamisel servadega saame sama graafi, mis on toodud joonisel 8.2.) Tugevalt sidusaid komponente on selles graafis aga tervelt neli: tipud A, B, C ja kõik nendega seotud kaared ning tipud D, E ja F igaüks eraldi. Tippe D, E ja F ühendavad kaared ei kuulu ühegi tugevalt sidusa komponendi koosseisu.

8.1.2 Puu

Puu (ingl tree) on sidus tsükliteta graaf.

Tegemist on mõnes mõttes piirjuhtumiga: puu on ühelt poolt minimaalne sidus graaf (ükskõik millise serva eemaldamine muudab puu mittesidusaks) ja teiselt poolt maksimaalne tsükliteta graaf (ükskõik millise uue serva lisamine tekitab tsükli).

Esimese väite kehtivuses veendumiseks vaatleme puu serva e = {u, v}. Oletame, et pärast selle serva eemaldamist on graaf endiselt sidus. See aga tähendab, et leidub mingi tee tipust u tippu v, mis ei läbi serva e. Lisades nüüd sellele teele serva e, saame tsükli. See on muidugi vastuolus eeldusega, et esialgne graaf oli tsükliteta, mistõttu peame järeldama, et sellist teed tipust u tippu v ei saa leiduda. Kuna arutelu ei sõltu serva e valikust, tähendab see, et puu muutub mittesidusaks ükskõik millise serva eemaldamisel.

Teise väite põhjendamine on sarnane: vaatleme puu tippe u ja v. Kuna puu on sidus, siis peab leiduma tee tipust u tippu v. See aga tähendab, et tippude u ja v vahele uue serva lisamine tekitaks tsükli. Kuna arutelu ei sõltu tippude u ja v valikust, tähendab see, et puusse tekib tsükkel mistahes serva lisamisel.

Programmeerimise seisukohalt pakuvad rohkem huvi juurega puud (ingl rooted tree). Juurega puu erineb tavalisest selle poolest, et üht selle tippu nimetatakse juureks (ingl root). Joonisel märgitakse juurtipp mõnikord rasvaselt, aga sagedamini paigutatakse tipud nii, et juurtipp on teistest kõrgemal, nagu näiteks tipud A, K ja S joonisel 8.4 toodud puudes.

Juurtipu esiletõstmine muudab puu hierarhiaks. Iga serva otstippudest on üks juurele lähemal kui teine. Juurele lähemat tippu nimetatakse teise ülemuseks (ingl parent), kaugemat tippu omakorda tema alluvaks (ingl child). Näiteks joonisel 8.4 vasakul toodud puus on tipp B tipu A alluv ja samal ajal tippude D ja E ülemus.

Puu tippu, millel on mõni alluv, nimetatakse sõlmeks (ingl inner node), alluvateta tippu aga leheks (ingl leaf). Näiteks joonisel 8.4 keskel kujutatud puus on K, M ja N sõlmed, aga L, O, P ja Q lehed.

Puu tippu koos tema kõigi (nii vahetute kui ka kaugemate) alluvatega nimetatakse alampuuks (ingl subtree). Näiteks joonisel 8.4 parempoolses puus moodustavad alampuu tipud T, V ja W. Muidugi on alampuu ka iga leht eraldi ja kogu puu tervikuna.

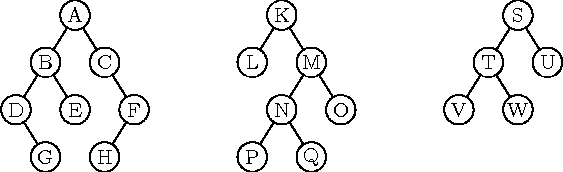
Joonis 8.4: Kahendpuude näiteid

Puud, mille igal sõlmel on maksimaalselt n alluvat, nimetatakse n-puuks. Näiteks kõik joonisel 8.4 kujutatud puud on kahendpuud (ingl binary tree). Puud, mille kõigil sõlmedel on sama arv alluvaid, nimetatakse homogeenseks. Näiteks joonisel 8.4 vasakul toodud puu ei ole homogeenne (tippudel C, D ja F on igaühel ainult üks alluv), aga keskmine ja parempoolne on.

Homogeenset puud, mille kõik lehed on juurest võrdsel kaugusel, nimetatakse täielikuks. Joonisel 8.4 kujutatud puudest pole ükski täielik, kuid parempoolset nimetatakse kompaktseks --- tal puuduvad täielikkusest vaid mõned lehed alumise tippuderea lõpust.

Kahendpuus on sageli kasulik eristatada, kas alluv on oma ülemuse vasak või parem alluv, isegi juhul kui tegu on ainsa alluvaga. Kahendpuu joonistamisel paigutatakse vasak alluv oma ülemusest madalamale ja vasakule, parem alluv aga vastavalt madalamale ja paremale. Seega on joonisel 8.4 vasakul kujutatud puus tipp F tipu C parem ja tipp H omakorda tipu F vasak alluv.

8.2 Puualgoritmid

8.2.1 Kahendpuu esitamine arvuti mälus

Kahendpuud on loomulik hoida rekursiivse struktuurina, kus iga tippu esitab kirje, milles on väljad selle tipu andmetega ja lisaks viidad selle tipu vasakule ja paremale alluvale. Kui tipul üht või teist (või ka mõlemat) alluvat pole, siis on vastavas väljas tühiviit. Kahendpuu loomuliku esituse näide on toodud joonisel 8.5.

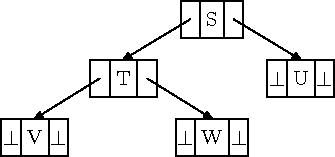
Joonis 8.5: Kahendpuu loomulik esitus

Teine võimalus on hoida kahendpuud massiivis, nagu näidatud joonisel 8.6: puu juur on massiivi elemendis a₁; elemendis a_i hoitava tipu alluvad on elementides a_2i ja a_2i+1 ning tema ülemus elemendis a_{ë i/2 û}.³

Massiiviesitus sobib hästi täielike ja kompaktsete kahendpuude hoidmiseks, sest siis täidab n-tipuline puu parajasti massiivi elemendid a_{1 ... n}.

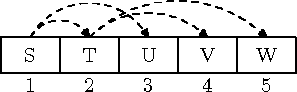
Joonis 8.6: Kompaktse kahendpuu massiiviesitus

Joonis 8.7: Mittetäieliku kahendpuu massiiviesitus

Nagu näha ka jooniselt 8.7, jääks mittetäieliku puu sellisel esitamisel osa massiivi elemente kasutamata. Esiteks oleks see muidugi asjatu mälukulu. Teiseks peaks me siis leidma mingi võimaluse neid tühje elemente tähistada, et me neid hiljem puu töötlemisel kogemata kasutada ei püüaks. Kuna joonisel näidatud nooled on vaid mõttelised seosed, mitte viidad, ei saa me nende puhul tühiviidaga võrdlemist kasutada!

8.2.2 Kahendpuu läbimine

Paljude puuülesannete lahendamisel on vaja puu tippe läbida mingis kindlas järjekorras. Vaatleme näiteks sellist ülesannet: antud puu, mille lehtedes on arvud; vaja on saada igasse sõlmtippu sellest algavas alampuus olevate lehtede arvude summa.

Muidugi saame igas sõlmes vajaliku summa leida tema vahetutes alluvates olevate arvude summana, aga seda ainult eeldusel, et alluvates on vajalikud summad juba välja arvutatud. See tähendab, et nõutud summade efektiivseks arvutamiseks tuleb iga tipu alluvad töödelda enne seda tippu ennast.

Puu niisugust läbimist nimetatakse lõppjärjestuses läbimiseks (ingl post-order traversal) ja selle üldkuju kahendpuude jaoks kirjeldab algoritm 1, mille täiendamine summaülesande lahenduseks oleks muidugi triviaalne.

Algoritm 1 LabiPuuLJ: Kahendpuu läbimine lõppjärjestuses
Sisend: t --- viit puu juurele, kus [[t]].v ja [[t]].p on vasak ja parem alampuu

kui t ¹ ^ --- tühja puu korral pole midagi läbida
LabiPuuLJ([[t]].v) --- töötleme vasaku alampuu
LabiPuuLJ([[t]].p) --- töötleme parema alampuu
--- siin töötleme tipu [[t]]
lõppkui

Kui summaülesandes liikus informatsioon puu läbimisel ``alt üles'' ja selle lahendamiseks oli vaja alluvad töödelda enne ülemust, siis paljudes teistes ülesannetes liigub informatsioon vastupidi, ``ülalt alla''.

Seda tüüpi ülesannete efektiivseks lahendamiseks on sageli mugavaim viis algoritm 2, puu läbimine eesjärjestuses (ingl pre-order).

Algoritm 2 LabiPuuEJ: Kahendpuu läbimine eesjärjestuses
Sisend: t --- viit puu juurele, kus [[t]].v ja [[t]].p on vasak ja parem alampuu

kui t ¹ ^ --- tühja puu korral pole midagi läbida
--- siin töötleme tipu [[t]]
LabiPuuEJ([[t]].v) --- töötleme vasaku alampuu
LabiPuuEJ([[t]].p) --- töötleme parema alampuu
lõppkui

Kolmandat klassikalist tehnikat kujutav algoritm 3 läbib kahendpuu tipud keskjärjestus (ingl in-order): kõigepealt vasaku alampuu, siis juurtipu ja lõpuks parema alampuu. Erinevalt kahest eelmisest on see meetod loomulikul viisil kasutatav ainult kahendpuude korral, sest üldisemal juhul pole selge, millise kahe alluva vahel peaks töötlema alampuu juurtipu.

Algoritm 3 LabiPuuKJ: Kahendpuu läbimine keskjärjestuses
Sisend: t --- viit puu juurele, kus [[t]].v ja [[t]].p on vasak ja parem alampuu

kui t ¹ ^ --- tühja puu korral pole midagi läbida
LabiPuuKJ([[t]].v) --- töötleme vasaku alampuu
--- siin töötleme tipu [[t]]
LabiPuuKJ([[t]].p) --- töötleme parema alampuu
lõppkui

Joonis 8.8 illustreerib ühe kahendpuu läbimist nende kolme algoritmi poolt: joonisel vasakul, keskel ja paremal on puu tipud nummerdatud vastavalt nende ees-, kesk- ja lõppjärjestuses läbimise järjekorras.

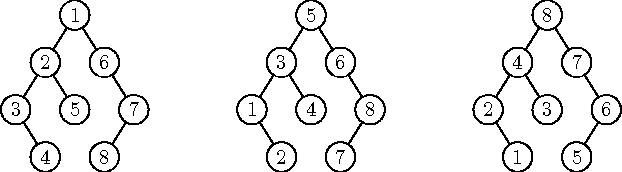
Joonis 8.8: Kahendpuu kolm läbimist

8.2.3 Kahendotsingu puu

Kahendpuud T nimetatakse kahendotsingu puuks (ingl binary search tree), ehk lühemalt otsingupuuks, kui (a) T on tühi või (b.1) vasaku alampuu kõigi tippude väärtused on juurtipu omast väiksemad ja (b.2) parema alampuu kõigi tippude väärtused juurtipu omast suuremad ja (b.3) kumbki alampuu on ka ise otsingupuu.⁴

Mingi väärtuse otsimine otsingupuus (algoritm 4) on sarnane kahendotsinguga järjestatud massiivis: igal sammul võrdleme otsitavat väärtust puu juurtipus olevaga; kui puu tipus olev väärtus on otsitavast väiksem, võime lisaks juurtipule edasise vaatluse alt välja jätta ka kogu vasaku alampuu, see tähendab jätkata otsimist paremas alampuus; kui puu juurtipus olev väärtus on otsitavast suurem, võime otsimist jätkata vasakus alampuus.

Algoritm 4 OtsiPuus: Otsimine otsingupuus
Sisend: t --- viit otsingupuu juurele; x --- otsitav väärtus
Väljund: Tagastab leitud kirje, või ^, kui x puus ei esine

kui t = ^
tagasta ^ --- tühjas puus ei leia midagi
muidukui x < [[t]].x
tagasta OtsiPuus([[t]].v, x)
muidukui x > [[t]].x
tagasta OtsiPuus([[t]].p, x)
muidu
tagasta t --- leidsime otsitava
lõppkui

Elemendi lisamine otsingupuusse (algoritm 4) on otsimisega üsna sarnane. See pole ka kuigi üllatav, sest algoritmi põhiline iva on uuele elemendile sobiva koha leidmine. Selle käigus saame ilma lisatööta tuvastada ka juhu, kui lisatav väärtus puus juba esineb.

Algoritm 5 LisaPuusse: Lisamine otsingupuusse
Sisend: t --- viit otsingupuu juurele; x --- lisatav väärtus
Väljund: Lisab väärtuse x puusse, kui see seal juba ei esine

kui t = ^
tee-uus t --- tühi puu, lisame uue lehe
[[t]].x¬x
[[t]].v¬^; [[t]].p¬^
muidukui x < [[t]].x
LisaPuusse([[t]].v, x)
muidukui x > [[t]].x
LisaPuusse([[t]].p, x)
muidu
--- väärtus juba on puus, pole midagi teha
lõppkui

Pole raske näha, et mõlema algoritmi keerukus on võrdeline leitud või lisatud tipu kaugusega puu juurtipust --- just nii palju kordi tuleb kummaski algoritmis teha rekursiivseid pöördumisi iseenda poole. Parimal juhul, kui töödeldav puu on täielik kahendpuu, on k-kihilises puus kokku n = 2^k - 1 tippu ja n-elemendilise andmehulga töötlemiseks kuluvad O(k) = O(logn) sammu on sel juhul kooskõlas juba varem viidatud kahendotsimise analoogiaga. Paraku kehtib see analoogia ainult selliste puude korral, mille iga tipu vasak ja parem alampuu on ligikaudu sama suured (sellisel juhul ütleme, et puu on tasakaalus).

Ilma spetsiaalseid pingutusi tegemata ei saa me üldjuhul eeldada, et meie otsingupuud tasakaalus püsivad. Näiteks elementide kasvavas või kahanevas järjekorras lisamisel saame tasakaalustatud puu asemel hoopis ahela, milles nii otsimine kui ka lisamine taanduvad lineaarseks ja võtavad O(logn) asemel O(n) operatsiooni.

Selleks, et otsingupuud töö käigus jooksvalt tasakaalus hoida (ja seda piisavalt efektiivselt teha), on välja mõeldud mitmeid kavalaid võtteid. Tuntumad neist on AVL-puud (ingl AVL-tree) ja puna-mustad puud (ingl red-black tree). Nende algoritmide detailne kirjeldus on aga käesoleva materjali jaoks natuke liiga pikk.

Antud väärtuse x eemaldamine otsingupuust on veidi keerulisem kui otsimine või lisamine. Kui me oleme eemaldatavat väärtust sisaldava tipu puust üles leidnud, on põhimõtteliselt kolm võimalust:

x asub lehes (näiteks x = 9, joonisel 8.9 vasakul); siis võime selle lehe lihtsalt puust eemaldada;
x asub ühe alluvaga sõlmes (x = 4, joonisel keskel); siis võime sõlme puust eemaldada ja tema ainsa alluva tema asemele panna (on lihtne veenduda, et puu jääb endiselt otsingupuuks);
x asub kahe alluvaga sõlmes (x = 5, joonisel paremal); siis ei saa me seda sõlme puust lihtsalt eemaldada, sest kahe vabaks jääva alluva hoidmiseks pole eemaldatava tipu ülemusel vabu viitasid; selle asemel leiame puust minimaalse eemaldatavast väärtusest suurema väärtuse x' (näites x' = 6), asendame eemaldatava väärtuse x tema asukohas väärtusega x' ja eemaldame selle asemel x' tema endisest asukohast (on lihtne veenduda, et puu jääb endiselt otsingupuuks; lisaks on lihtne veenduda, et x' ei saa asuda kahe alluvaga sõlmes, seega tema kustutamiseks pole enam vaja suuruselt järgmist elementi otsida; algoritmi õigsuse seisukohalt pole viimane ajaolu oluline).

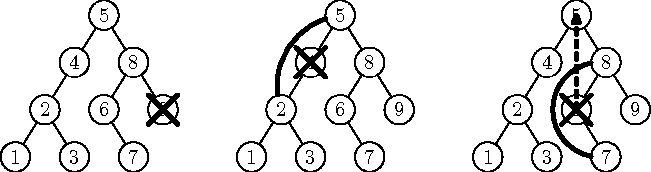
Joonis 8.9: Elemendi eemaldamine otsingupuust

Algoritm 6 EemaldaPuust: Eemaldamine otsingupuust
Sisend: t --- viit otsingupuu juurele; x --- eemaldatav väärtus
Väljund: Eemaldab väärtuse x puust, kui see seal esineb

kui t = ^
--- tühi puu, pole midagi teha
muidukui x < [[t]].x
EemaldaPuust([[t]].v, x)
muidukui x > [[t]].x
EemaldaPuust([[t]].p, x)
muidu --- vaja on eemaldada tipp t
kui [[t]].p = ^
t'¬t; t¬[[t]].v --- haagime t puust lahti
kustuta t' --- ja kustutame mälust
muidu
[[t]].x¬Minimaalne([[t]].p) --- asendame naaberväärtusega
EemaldaPuust([[t]].p, [[t]].x) --- ja eemaldame vana eksemplari
lõppkui
lõppkui

Algoritm 7 Minimaalne: Leiab otsingupuust minimaalse väärtuse
Sisend: t --- viit otsingupuu juurele, ei või olla ^

kui [[t]].v = ^
tagasta [[t]].x
muidu
tagasta Minimaalne([[t]].v)
lõppkui

Teema lõpetuseks võiks veel märkida, et otsingupuu läbimisel keskjärjestuses külastame selle tippe nende väärtuste kasvamise järjekorras. See omadus järeldub üsna lihtsalt otsingupuu definitsioonist.

8.2.4 Kahendkuhi

Puud nimetatakse kuhjaks (ingl heap), kui tema ühegi tipu väärtus ei ületa selle tipu vahetu ülemuse väärtust. Kahendpuud, mis on samal ajal ka kuhi, nimetatakse muidugi kahendkuhjaks.

Vahetult kuhja definitsioonist järeldub, et mistahes kuhjas peab maksimaalse väärtusega element asuma juurtipus. See tähelepanek ongi aluseks, et konstrueerida kahendkuhjal põhinev andmestruktuur, millesse saab efektiivselt andmeid juurde lisada ja suvalisel hetkel kiiresti leida parasjagu kuhjas olevate elementide maksimumi.

Kuhja selliseks kasutamiseks on otstarbekas hoida kuhja elemente kompaktse kahendpuu massiiviesitusena. Uue elemendi lisamisel kuhja lisame selle kõigepealt massiivi lõppu (mis selle massiivi puuna tõlgendamise terminites tähendab, et me lisame puule uue lehe; joonisel 8.10 vasakul). Muidugi võib juhtuda, et uus leht ei rahulda kuhja tingimust.

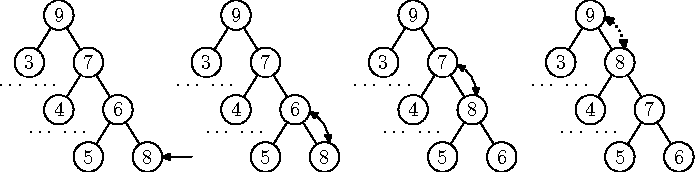
Joonis 8.10: Elemendi lisamine kahendkuhja

Kuhja taastamiseks hakkame lisatud elementi puus ülespoole nihutama. Kui uus leht on oma ülemusest suurem, siis võime need kaks lelementi lihtsalt omavahel vahetada --- siis on kuhja omadus vähemalt selles paaris taas rahuldatud. Kui vastlisatud element on suurem ka oma uuest ülemusest, vahetame ta veelkord ülespoole --- nii jätkame, kuni ühel hetkel jõuame piisavalt suure ülemuseni või kuni uus element jõuab puu juurtippu.

Ei tohiks olla raske veenduda, et kui esialgne puu oli kuhi, siis on seda ka uue elemendi üles viimisel saadud puu.

Algoritm 8 ViiUles: Viib kahendkuhja lisatud lehe selle õigele kohale
Sisend: a_{1 ... n} --- puu massiiviesitus, kus a_{1 ... n-1} moodustavad kuhja
Väljund: a_n viidud kuhjas oma õigele kohale

i¬n
senikui i > 1
--- invariant: a_1..n miinus a_i alampuu on kuhi Ù a_i alampuu on kuhi
k¬ë i / 2 û
kui a_k < a_i
a_i«a_k --- a_i on oma ülemusest suurem, tõrjub selle allapoole
lõppkui
i¬k
lõppsenikui

Kuhjast maksimaalse elemendi väljavõtmisel tekib samasugune probleem nagu otsingupuust elemendi eemaldamisel --- me ei saa eemaldatud elemendi kohta tühjaks jätta. Esimene mõte --- tuua juurtipu uueks väärtuseks tema kahest alluvast suurem --- ei ole pikas perspektiivis hea lahendus, sest siis võib uus vaba koht puu lehtede hulgas tekkida ükskõik kuhu ja järgmisel lisamisel on raske seda leida.

Selleks, et vaba koht jääks kindlasti puu massiiviesituse lõppu, toome puu juurtipu uueks väärtuseks justnimelt massiivi viimase elemendi (ja selle koht omakorda jääb vabaks; joonisel 8.11 vasakul). Kuna see on puu leht ja seega üsna väikese väärtusega, on tõenäoline, et sellega saab jälle puu kuhjaomadus rikutud.

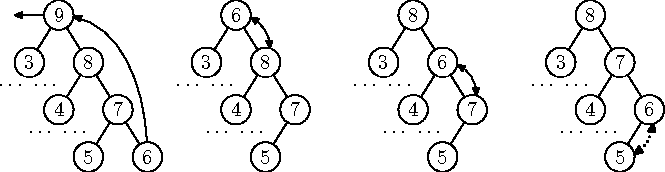
Joonis 8.11: Elemendi eemaldamine kahendkuhjast

Kuhja taastamiseks hakkame nüüd vastset juurtipu kuhjas allapoole viima: igal sammul valime uue elemendi ja tema alluvate hulgast maksimaalse ning tõstame selle lokaalseks ülemuseks. Nagu elemendi üles viimisel, järgneme ka seekord vahetuse korral uuele elemendile ja jätkame võrdlemist ja vahetamist, kuni puu on taas kuhi.

Algoritm 9 ViiAlla: Viib kahendkuhja lisatud juure selle õigele kohale
Sisend: a_{1 ... n} --- puu massiiviesitus, kus a_{2 ... n} moodustavad kaks kuhja
Väljund: a₁ viidud kuhjas oma õigele kohale

i¬1
senikui i < n
--- invariant: a_{1 ... i} on kuhi Ù a_i alampuu oleks kuhi, kui a_i oleks ¥
k¬i
kui 2 · i £ n Ù a_{2 · i} > a_k
k¬2 · i
lõppkui
kui 2 · i + 1 £ n Ù a_{2 · i + 1} > a_k
k¬2 · i + 1
lõppkui
kui k > i
a_i«a_k --- a_i on oma alluvast väiksem, see tõrjub ta allapoole
lõppkui
i¬k
lõppsenikui

Kahe eeltoodud võtte kombineerimisel saame efektiivse algoritmi massiivide sortimiseks: kõigepealt muudame massiivi kuhjaks, ``lisades'' selle elemente järjest kuhja, mida hoiame sama massiivi algusosas; seejärel võtame kuhjast maksimaalse elemendi, taastame kuhja, võtame allesjäänutest maksimaalse, taastame uuesti kuhja, ja nii edasi, kuni olemegi kõik elemendid järjestanud.

Algoritm 10 KuhjaSort
Sisend: a_{1 ... n} --- töödeldav massiiv
Väljund: a_{1 ... n} --- väärtused vahetatud nii, et " i < n : a_i £ a_i+1

--- muudame massiivi kuhjaks
korda i¬1 ... n
--- invariant: a_{1 ... i-1} juba on kuhi
ViiUles(a_{1 ... i})
lõppkorda
--- muudame kuhja järjestatud massiiviks
korda i¬n ... 1
--- invariant: a_{1 ... i} on kuhi
a_i«a₁
ViiAlla(a_{1 ... i - 1})
--- vahetingimus: a_i £ a_i+1 £ ... £ a_n
lõppkorda

Kuna n-tipulises kompaktses puus võib element nii üles kui alla liikuda ülimalt O(logn) sammu, saame kummagi korduse ajalise keerukuse hinnanguks O(n logn).

8.3 Graafialgoritmid

8.3.1 Graafi esitamine arvuti mälus

Kaks tähtsamat võtet graafide esitamiseks arvuti mälus on naabrusmaatriks ja kaareloendid. Mõlemad võtted sobivad paremini orienteeritud graafide esitamiseks. Orienteerimata servi esitatakse tavaliselt kahe vastassuunalise kaarena. See tähendab, et iga serva {v₁, v₂} asemel pannakse graafi kaks kaart (v₁, v₂) ja (v₂, v₁). Kui pidada silmas ainult graafi ühelt tipult teisele liikumise võimalikkust, siis ei muuda selline asendus midagi. Kui aga mõnes ülesandes on vaja servi graafist eemaldada või vältida sama serva korduvat läbimist, tuleb sellised paariskaared kuidagi eraldi tähistada.

Graafi G naabrusmaatriks (ingl adjacency matrix) on ruutmaatriks, milles on üks rida ja üks veerg graafi G iga tipu kohta. Tipule v₁ vastava rea ja tipule v₂ vastava veeru ristumiskohas on info kaare (v₁, v₂) kohta.

Sellist maatriksit on kõige mugavam hoida 2-mõõtmelise massiivina. Lihtsaimal juhul on massiivi elemendid tõeväärtused või täisarvud, ning kaare olemasolu tähistab siis väärtus 1 ja selle puudumist väärtus 0 massiivi vastavas elemendis (nagu näha joonisel 8.12 toodud näites). Vajadusel võib luua ka massiivi, mille elemendid on keerukamad kirjed, ja hoida iga kaare kohta rohkem andmeid.

Täielikult orienteerimata graafi puhul kasutatakse naabrusmaatriksi asemel mõnikord ``naabruskolmnurka'' --- maatriksist on kasutusel ainult selle peadiagonaali kohal olev osa. Kuna orienteerimata graafi naabrusmaatriks on alati peadiagonaali suhtes sümmeetriline, siis pole sel juhul diagonaali alla jääva osa andmetega täitmine vajalik.

Joonis 8.12: Segagraaf ja tema naabrusmaatriks

Graafi esitus kaareloenditena (ingl adjacency-lists representation) annab iga tipu kohta sellest tipust väljuvate servade loetelu.

Selliseid loetelusid on tavaliselt mugav hoida lihtahelates, ja kogu graafi esitus koosneb siis massiivist või ahelast, milles on üks element graafi iga tipu kohta. Lisaks otseselt tipu enda andmetele sisaldab see element ka viita tipust väljuvate servade loetelule (nagu näha joonisel 8.13 toodud näites), ja iga serva element omakorda viitab mingil viisil selle serva lõpptipule.

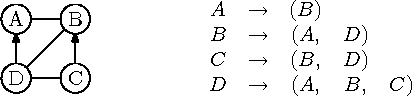
Joonis 8.13: Segagraaf ja tema kaareloendid

Kaareloendeid on parem kasutada sellistes algoritmides, kus on vaja kiiresti leida kõik antud tipust väljuvad kaared (või kõik tipud, kuhu antud tipust edasi liikuda saab). Naabrusmaatriksid on tõhusamad algoritmides, kus on vaja kiiresti kontrollida, kas kahe antud tipu vahel on kaar või mitte.

Mälukasutuse seisukohalt on naabrusmaatriksid efektiivsemad tihedate ja kaareloendid hõredate graafide esitamisel.⁵

8.3.2 Graafi läbimine laiuti

Nagu puude korral, nii on ka paljude graafiülesannete lahenduse võti graafi tippude (ja servade) õiges järjekorras läbimises. Sageli osutub selleks õigeks järjekorraks graafi läbimine laiuti (ingl breadth-first search).

Laiuti läbimine (algoritm 11) algab mingist lähtetipust (joonisel 8.14 tipp A) ja vaatleb juba leitud tippudest väljuvaid servi või kaari, et leida uusi, seni avastamata tippe.⁶ Uusi tippe töödeldakse nende avastamise järjekorras, seetõttu moodustavad avastatud, aga veel töötlemata tipud (algoritmis järjekorra Q sisu, joonisel tähistatud helehalliga) lähtetipu ümber omamoodi ``laineharja'' või ``rindejoone'', mis sellest igas suunas võrdse kiirusega eemaldub. Viimase asjaolu järgi ongi laiuti läbimine oma nime saanud.

Algoritm 11 LabiGraafL: Läbib graafi laiuti, alustades antud tipust
Sisend: graaf G; lähtetipp v₀ Î V(G)
Abimuutujad: G iga tipu v jaoks abimuutuja v.olek; tippude järjekord Q

korda v Î V(G) --- kõik V tipud
v.olek¬valge
lõppkorda
Q¬v₀; v₀.olek¬hall
senikui Q ¹ Ø --- järjekord pole tühi
v¬Q --- võtame järjekorra esimese elemendi
korda w Î V(v) --- kõik v naabertipud
kui w.olek = valge --- uus tipp
Q¬w; w.olek¬hall
lõppkui
lõppkorda
v.olek¬must --- v töödeldud
lõppsenikui

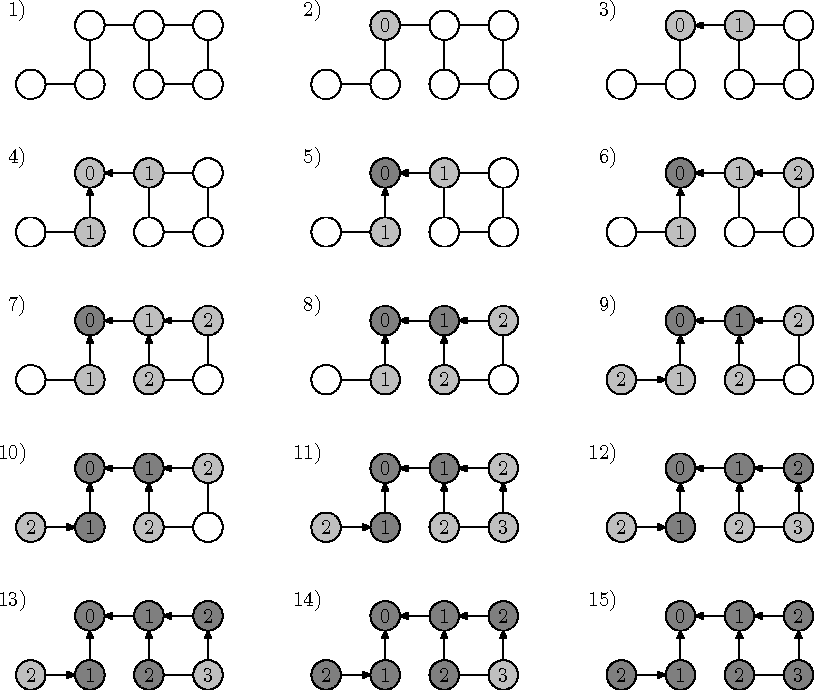
8.3.3 Lühima tee leidmine

Sidusa graafi laiuti läbimisel tippude avastamiseks kasutatud servad (joonisel 8.14 märgitud paksema joonega) moodustavad selle graafi toesepuu (ingl spanning tree) --- puu, mille tippude hulk langeb kokku graafi G tippude hulgaga ja mille servade hulk on graafi servade hulga alamhulk.

Graafil võib olla mitmeid erinevaid toesepuid, kuid just laiuti läbimisel saadud toesepuu kasulik omadus on, et igast tipust mööda sellesse puusse kuuluvaid servi lähtetippu viiv tee ongi minimaalse võimaliku pikkusega, kui me loeme tee pikkuseks sellele jäävate servade arvu. Seega on graafis lühimate teede leidmiseks vaja laiuti läbimist vaid minimaalselt modifitseerida.

Algoritm 12 LyhTeed: Leiab lühimad teed, alustades antud tipust
Sisend: graaf G; lähtetipp v₀ Î V(G)
Abimuutujad: G iga tipu v jaoks abimuutujad v.kaug ja v.eelm;
tippude järjekord Q

korda v Î V(G) --- kõik V tipud
v.kaug¬¥
lõppkorda
Q¬v₀; v₀.kaug¬0; v₀.eelm¬^
senikui Q ¹ Ø --- järjekord pole tühi
v¬Q --- võtame järjekorra esimese elemendi
korda w Î V(v) --- kõik v naabertipud
kui w.kaug = ¥ --- uus tipp
Q¬w; w.kaug¬v.kaug + 1; w.eelm¬v
lõppkui
lõppkorda
lõppsenikui

Algoritmi 12 õigsuse põhjendamiseks paneme tähele, et

läbimise algatamine real 4 on ilmselt õige, sest lähtetipu v₀ kaugus iseendast on 0;
real 5 algav kordus töötleb graafi tippe nende lähtetipust kaugenemise järjekorras; täpsemalt, kõik tipud, mille kaugus lähtetipust on k töödeldakse enne kui ükski tipp, mille kaugus on k+1;
viitade v_k.eelm = v_k-1, v_k-1.eelm = v_k-2, ..., v₁.eelm = v₀ poolt näidatav tee mistahes tipust v_k lähtetippu v₀ on minimaalse sammude arvuga; kui see nii ei oleks, siis peaks sellel teel leiduma tipp v_i, mille viit v_i.eelm osutab tipule v_i-1 ja millel on olemas ka naaber v_j, mille kaugus lähtetipust on väiksem kui i-1; siis aga oleks v_j töödeldud enne kui v_i-1 ja tipp v_i avastatud serva {v_j, v_i} kaudu; kuna seda ei juhtunud, siis järelikult sellist tippu v_j ei ole, ja leitud tee ongi lühim võimalik.

Kuna algoritm töötleb graafi G iga tippu täpselt ühe korra ja vaatleb iga serva täpselt kaks korda, siis kulub N tipu ja M servaga graafi töötlemiseks kokku O(N+M) operatsiooni.

Selle algoritmi tööd illustreerib joonis 8.15, kus tippudele on märgitud nende kaugused lähtetipust ja nooled osutavad igast tipust tema ülemusele toesepuus.

Teema lõpetuseks võiks veel märkida, et algoritmi 12 on võimalik üldistada ka juhule, kui graafi servadele on antud mittenegatiivsed kaalud ja tee pikkuseks loetakse mitte teel olevate servade arvu, vaid nende kaalude summat. Seda üldistust tuntakse autori järgi Dijkstra algoritmi nime all, aga selle täpsemaks kirjeldamiseks ja põhjendamiseks ei jätku siinkohal ruumi.

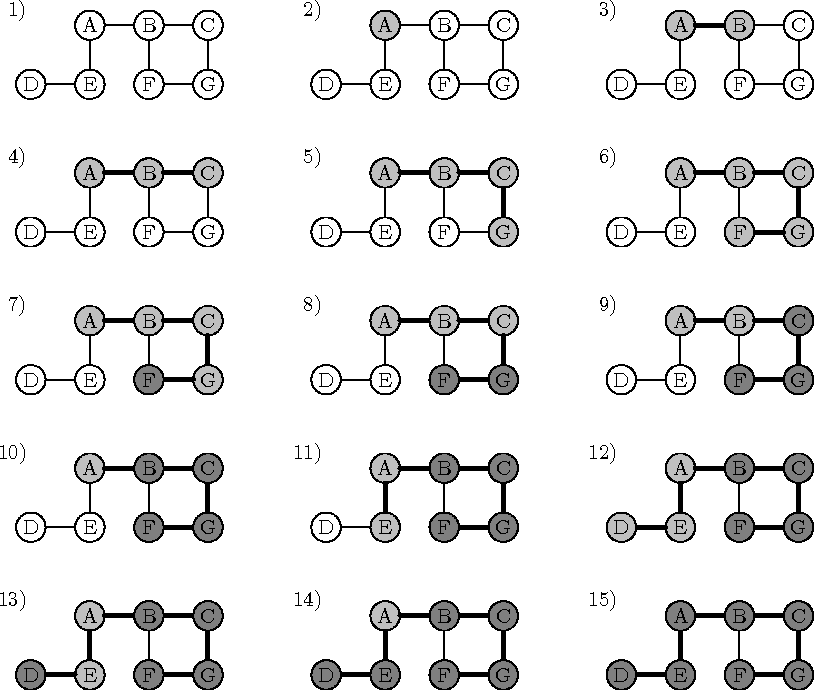
8.3.4 Graafi läbimine sügavuti

Laiuti läbimise kõrval on teine tähtsam viis graafi töötlemiseks selle läbimine sügavuti (ingl depth-first search). Sarnaselt laiuti läbimisega algab ka sügavuti läbimine (algoritmid 13 ja 14) mingist lähtetipust ja vaatleb uute tippude leidmiseks juba avastatud tippudest väljuvaid servi või kaari. Erinevus seisneb selles, et iga uue tipu avastamisel töödeldakse sellest tipust algav ``haru'' enne järgmise juurde asumist lõpuni.

Algoritm 13 LabiGraafS: Läbib graafi sügavuti, alustades antud tipust
Sisend: graaf G; lähtetipp v₀ Î V(G)
Abimuutujad: G iga tipu v jaoks abimuutuja v.olek, v.alust, v.lopet;
globaalne loendur t

korda v Î V(G) --- kõik V tipud
v.olek¬valge
lõppkorda
t¬0
TootleTippS(v₀)

Algoritm 14 TootleTippS: Läbib sügavuti antud tipu ``alampuu''
Sisend: v Î V(G)

v.olek¬hall; t¬t+1; v.alust¬t --- v töötlemise algus
korda w Î V(v) --- kõik v naabertipud
kui w.olek = valge --- uus tipp
TootleTippS(w)
lõppkui
lõppkorda
v.olek¬must; t¬t+1; v.lopet¬t --- v töötlemise lõpp

Sarnaselt laiuti läbimisega eraldab ka sügavuti läbimine töödeldavast graafist toesepuu, aga see puu hoopis teise kujuga (vrdl jooniseid 8.14 ja 8.16). Sarnaselt laiuti läbimisega on ka sügavuti läbimise keerukus O(N+M).

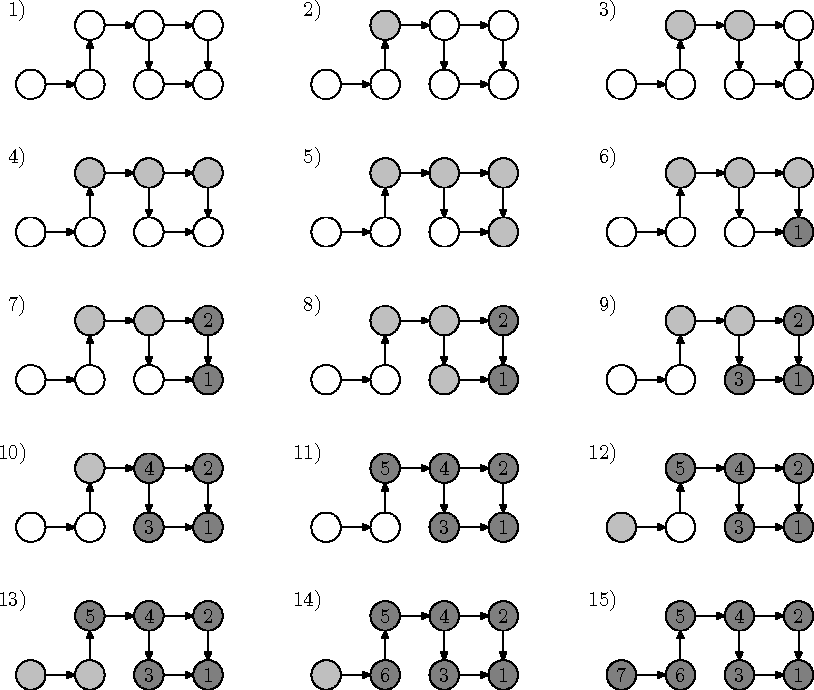
8.3.5 Topoloogiline sorteerimine

Paljudes sügavuti läbimisel põhinevates algoritmides on kasulik tähele panna iga tipu töötlemise alguse (algoritmi 14 rida 1) ja lõpu (rida 7) aega. Nende aegade omavahelised suhted erinevate tippude vahel on tihedalt seotud graafi läbimise käigus eraldatava toesepuu struktuuriga.

Üks ülesandeid, mille lahendamisel tippude läbimise aegade võrdlemine kasuks tuleb, on suunatud graafi tippude sorteerimine topoloogilisse järjekorda (ingl topological order). Topoloogiliseks nimetatakse graafi tippude järjestust, mille korral kõik kaared osutavad järjekorras eespool olevatelt tippudelt tagapool olevatele, aga mitte kunagi vastupidi.

Topoloogilist sorteerimist on vaja näiteks üksteisest sõltuvate tööde järjekorra planeerimisel: kui me esitame iga töö graafi tipuna ja tõmbame igasse tippu kaared kõigist neist, mis peavad enne selle töö alustamist tehtud olema, siis saame töid topoloogilises järjekorras ette võttes kõik õigesti tehtud.

Algoritm 15 TopoSort: Leiab suunatud graafis topoloogilise järjestuse
Sisend: graaf G
Abimuutujad: G iga tipu v jaoks abimuutuja v.olek; tippude magasin S

korda v Î V(G) --- kõik V tipud
v.olek¬valge
lõppkorda
S¬Ø
korda v Î V(G) --- kõik V tipud
kui v.olek = valge --- uus juurtipp
TopoTipp(w)
lõppkui
lõppkorda
senikui S ¹ Ø --- magasin pole tühi
v¬S --- võtame magasini tipmise elemendi
väljasta v
lõppsenikui

Algoritm 16 TopoTipp: Läbib sügavuti antud tipu ``alampuu''
Sisend: v Î V(G)

v.olek¬hall
korda w Î V(v) --- kõik v naabertipud
kui w.olek = valge --- uus tipp
TopoTipp(w)
lõppkui
lõppkorda
v.olek¬must; S¬v --- töödeldud tipp magasini

Algoritmi 15 õigsuse põhjendamiseks tuleb tähele panna, et

väljakutse TopoTipp(v) töötleb kõik need tipud, mis on tipust v graafi servi (või kaari) pidi liikudes saavutatavad ja mis veel ei ole töödeldud;
seega on väljakutse TopoTipp(v) täitmise lõpuks töödeldud kõik need tipud, mis ei tohi topoloogilises järjestuses tipust v eespool olla;
seega tuleks topoloogilise järjestuse saamiseks tipud väljastada nende töötlemise lõpuaegade kahanemise järjekorras;
seda aga TopoSort teebki, kuna TopoTipp väljakutsed panevad tipud nende töötlemise lõppedes magasini ja TopoSort väljastab nad magasinist väljavõtmise järjekorras (mis vastavalt magasini definitsioonile on vastupidine nende magasini panemise järjekorrale.

Algoritmi 15 tööd illustreerib joonis 8.17.

Muidugi ei saa topoloogiliselt järjestada graafi, milles on tsüklid. Näiteks graafis G=(V,E), kus V={A,B,C} ja E={(A,B), (B,C), (C,A)}, ei saa ükski tipp ei saa olla topoloogilises järjekorras esimene. Osutub, et efektiivne viis graafi tsüklilisuse kontrollimiseks ongi püüda teda topoloogiliselt sorteerida ja kontrollida, et selle käigus vastuolu ei teki.

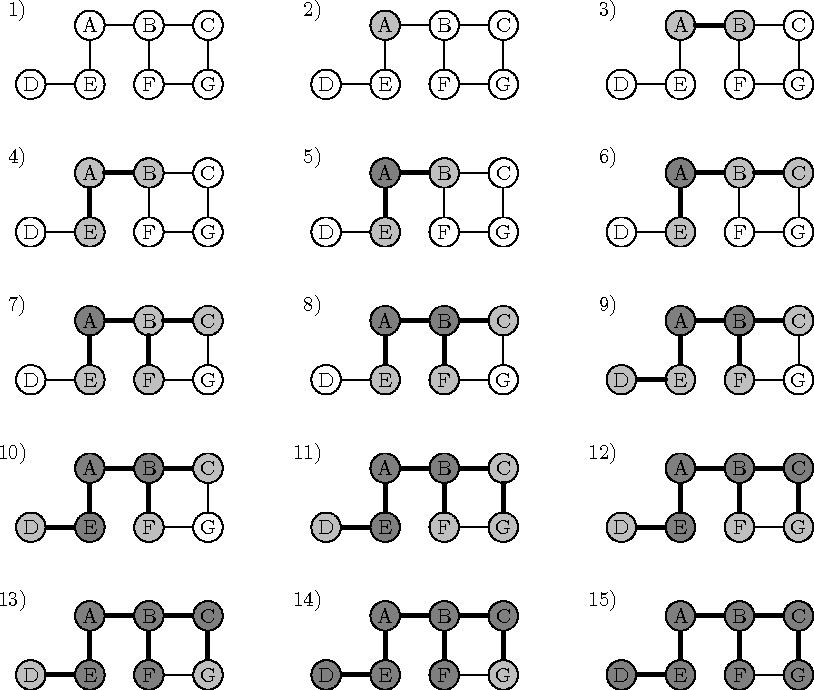
Joonis 8.14: Graafi läbimine laiuti

Joonis 8.15: Lühimate teede leidmine graafis

Joonis 8.16: Graafi läbimine sügavuti

Joonis 8.17: Graafi topoloogiline sorteerimine

Ülesanded

Ülesanne 1 Kirjutada alamprogramm TrykiPuu, mis saab kahendpuu loomuliku esituse ja väljastab suluavaldise, mis sobib selle puu uuesti sisselugemiseks näidete hulgas toodud alamprogrammi LoePuu abil. (Vihje: millises järjekorras peavad puu tipud selles suluavaldises olema?)

Ülesanne 2 Koostada algoritm ja kirjutada programm loomulikus esituses antud kahendpuu tippude läbimiseks ``sügavuse järjekorras'': kõigepealt juurtipp, siis selle vahetud alluvad, siis nende vahetud alluvad jne. Näiteks kõigis kolmes joonisel 8.4 toodud puus tuleks tipud läbida nende märgendite tähestikulises järjekorras.

Ülesanne 3 Koostada algoritm, mis leiab naabrusmaatriksina antud suunatud graafi iga tipu jaoks temast väljuvate ja temasse sisenevate kaarte arvu. Milline on selle algoritmi tööaeg N tipu ja M servaga graafi töötlemisel?

Kohandada see algoritm kaareloenditena antud graafile. Milline on tema tööaeg nüüd?

Ülesanne 4 Koostada laiuti läbimisel põhinev algoritm ja kirjutada selle alusel programm, mis leiab naabrusmaatriksina antud suunamata graafi sidususkomponendid. Vastusena väljastada komponentide arv ja igasse komponenti kuuluvate tippude loetelu.

Ülesanne 5 Millise tulemuse annab algoritmi 15 rakendamine suunatud graafile, milles on tsükkel? Täiendada õppematerjali lisas toodud programmi TopoSort nii, et tsükleid sisaldava graafi töötlemisel oleks tulemuseks asjakohane veateade.

Kirjandus

Kõik eelmises peatükis viidatud materjalid käsitlevad vähemalt mingil määral ka mittelineaarseid struktuure. Samuti võib puude ja graafidega seotud peatükke leida paljudest kombinatoorikaõpikutest, sealhulgas ka käesoleva õppevahendi kombinatoorikateemas viidatavatest. Seetõttu on allpool välja toodud vaid mõned konkreetselt graafiteooriale keskenduvad õpikud.

Peeter Puusemp. Graafiteooria elemente. Tallinna Tehnikaülikool, 2000.: Üldine sissejuhatus graafiteooriasse. 96 lk.
Ahto Buldas, Peeter Laud, Jan Villemson. Graafid. Tartu Ülikool, 2003.: Üldine sissejuhatus graafiteooriasse. 92 lk.
Oystein Ore. Graafid ja nende kasutamine. Valgus, 1976.: Keskendub rohkem graafiteooria matemaatilisele poolele, programmeerimisele eriti tähelepanu ei pööra. 139 lk.
Frank Harary. Graph Theory. Addison-Wesley, 1969.: Klassikaline graafiteooria õpik, samuti matemaatilise kallakuga. 274 lk.
Reinhard Diestel. Graph Theory. Springer, 2000.: Üsna uus klassikalise graafiteooria õpik. 315 lk.
http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/

1: Teede, ahelate ja tsüklitega seonduv terminoloogia ei ole graafiteoorias väga hästi standardiseeritud, seetõttu tuleb enne põhjalikumate järelduste tegemist uurida, kuidas konkreetse raamatu autor need terminid enda jaoks defineerinud on. Näiteks kasutatakse mõnes ingliskeelses raamatus sõna `path' meie `ahela' tähenduses ja meie `tee' jaoks sel juhul otsest vastet polegi. Mingil määral kehtib sama ka graafi enda mõiste kohta. Näiteks nimetatakse paljudes raamatutes graafideks ainult selliseid, milles mistahes kahe tipu vahel võib olla ülimalt üks serv ja silmused pole üldse lubatud. Programmeerimises tavaliselt graafidele selliseid piiranguid ei seata.
2: Peaks olema ilmne, et suunamata graafis langevad sidususe ja tugeva sidususe mõisted kokku, mistõttu sel juhul pole tugeva sidususe ja tugevalt sidusa komponendi mõiste järele vajadust.
3: Kirjutis ë i/2 û tähendab, et jagamisel tuleb võtta jagatise täisosa.
4: See definitsioon eeldab, et puus ei ole korduvaid väärtusi. Sellest eeldusest loobumisel peame täpsustama, kuidas me korduvaid väärtusi hoida tahame, ja muidugi ka järgnevaid algoritme vastavalt täiendama.
5: Tihedaks (ingl dense) nimetatakse graafi, mille mille tipupaaridest enamik on omavahel ühendatud. Hõredaks (ingl sparse) nimetatakse graafi, mille tipupaaridest enamik on omavahel ühendamata.
6: Siin ja ka järgnevates näidetes eeldame, et igast tipust väljuvaid servi vaadeldakse naabertippude nimede tähestikulises järjekorras. Algoritmid töötavad õigesti ka ilma selle eelduseta, aga näited tuleks teise läbivaatusjärjekorra puhul veidi erinevad.