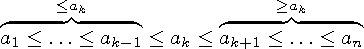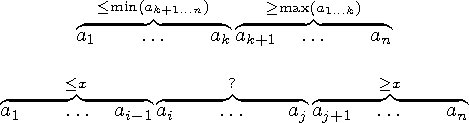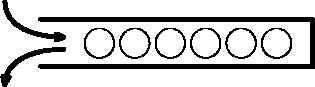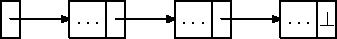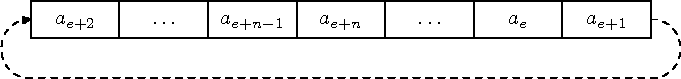Peatükk 7 Lineaarsed andmestruktuurid
Käesolevas peatükis tutvume andmestruktuuri mõistega ning vaatleme tähtsamaid lineaarseid andmestruktuure ja nendega seotud algoritme.
7.1 Andmestruktuuri mõiste
Andmestruktuur (ingl data structure) on vahend suure hulga (tavaliselt samatüübiliste) andmete hoidmiseks ja neile efektiivse juurdepääsu korraldamiseks.
Käesolevas peatükis vaadeldavaid struktuure ühendab asjaolu, et nende sisu saab esitada lineaarse elementide loendina. Seetõttu kasutataksegi nende struktuuride kohta ühist nimetajat ``lineaarne''.
7.2 Madalama taseme struktuurid
Esimeste struktuuridena võtame vaatluse alla massiivi ja lihtahela. Neid võib pidada madalama taseme struktuurideks, kuna neid kasutatakse sageli abivahendina keerulisemate ja abstraktsemate struktuuride realiseerimisel.
Muidugi ei maksa sellest järeldada, et pole rakendusi, kus just massiiv või lihtahel ongi sobivaimad struktuurid. Neid on piisavalt.
Nagu juba varem märgitud, on massiiv ühetüübiliste elementide kogum, kus iga elementi identifitseerib täisarvuline indeks (mitmemõõtmelise massiivi korral vastavalt üks indeks iga mõõtme kohta).
Massiivi kui andmestruktuuri iseloomustavad järgmised omadused:
-
Massiivi suurus on tavaliselt fikseeritud. Keeltes, kus massiivi suurust pärast massiivi loomist üldse muuta saab, on see üsna ajamahukas operatsioon (oluliselt ei peta ettekujutus, et selleks tehakse uus massiiv, kopeeritakse vana massiivi kõik elemendid uude ümber ja kustutatakse vana massiiv mälust ära). Paljudes keeltes pole massiivi suuruse muutmine pärast selle loomist enam võimalik.
Kui on siiski vaja massiivi omadustega andmestruktuuri, mille elementide arv pole kohe teada, on üks võimalus luua maksimaalse vaja minna võiva suurusega massiiv ja pidada eraldi muutuja abil arvet selle üle, kui suur osa massiivist tegelikult kasutusel on.
- Massiivi elemendi leidmine tema indeksi järgi on kiire operatsioon ja selleks tehtava töö maht ei sõltu massiivi suurusest. Selle operatsiooni ajakulu sõltub tavaliselt massiivi mõõtmete arvust, aga on igal juhul tühine võrreldes kõigi keerulisemate struktuuridega.
- Massiivi elemendi väärtuse väljavahetamine (massiivi elemendile uue väärtuse omistamine) on tavaline omistamistehe ja selleks tehtava töö maht (kui element on indeksi järgi juba leitud) ei sõltu massiivi suurusest ega selle mõõtmete arvust.
- Vaadeldes muutuva suurusega massiive, on võimalik rääkida ka massiivi elementide lisamisest ja eemaldamisest.
Kui kõigi olemasolevate elementide järjekord peab säilima, on massiivist elemendi eemaldamine või uue lisamine üsna kallis operatsioon. Elemendi lisamisel tuleb uuele elemendile teiste vahele ruumi tegemiseks kõiki temast tahapoole jäävaid elemente nihutada ühe koha võrra massiivi lõpu suunas (joonis 7.1 (a)). Olemasoleva elemendi eemaldamisel tekkinud tühimiku täitmiseks tuleb kõiki temast tahapoole jäävaid elemente nihutada massiivi alguse suunas (joonis 7.1 (b)). Nagu jooniselt näha, on n-elemendilise massiivi i. elemendi lisamisel või eemaldamisel selleks tehtava töö maht Q(n - i).
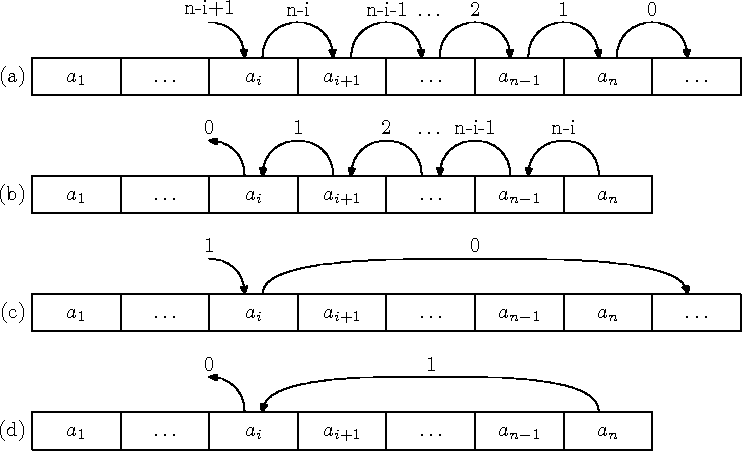
Joonis 7.1: Elemendi massiivi lisamine ja massiivist eemaldamine
Kui olemasolevate elementide järjekorra säilimine pole oluline, saab nii uue elemendi antud positsioonile lisamise kui ka elemendi eemaldamise realiseerida konstantse töömahuga (joonis 7.1 (c) ja (d)).
Kui indeksi järgi elemendi leidmine on massiivis väga efektiivne standardoperatsioon, siis elemendi järgi indeksi leidmine (ehk antud väärtuse otsimine massiivi elementide hulgast) pole üldiselt kumbagi: üldjuhul ei saa seda teha efektiivselt ja seetõttu pole see operatsioon sageli ka programmikeele standardvahendite hulgas.
Ilma massiivi elementidele täiendavaid tingimusi kehtestamata on ainus võimalus antud väärtuse leidmiseks (või veendumiseks, et seda väärtust massiivi elementide hulgas üldse ei leidu) kõik massiivi elemendid järjest läbi vaadata. Sellist meetodit nimetatakse lineaarseks otsinguks (ingl linear search).
Algoritm 1
LinOtsV: Lineaarne otsing massiivis
Sisend: a1 ... n --- antud massiiv; x --- otsitav väärtus
Väljund: tagastab leitud elemendi indeksi, või n+1, kui x massiivis ei esine
Abimuutujad: i Î N --- uuritava elemendi indeks
-
korda i¬1 ... n
-
--- invariant: a1 ... i-1 otsitavat väärtust ei sisalda
-
kui ai = x
-
--- otsitav väärtus leitud, tagastame selle indeksi
-
tagasta i
-
lõppkui
-
lõppkorda
-
--- vahetingimus: a1 ... n otsitavat väärtust ei sisalda
-
tagasta n+1
Muidugi pole raske näha, et selle algoritmi keerukus on parimal juhul Q(1) (kui otsitav väärtus on a1) ja halvimal juhul Q(n) (kui otsitav väärtus on an või ei esine massiivis üldse).
Veidi keerukam on hinnata keskmist keerukust. Selleks peame kõigepealt tegema mingi eelduse erinevate väärtuste jaotumise kohta massiivis. Muude andmete puudumisel on kõige loomulikum eeldada, et otsitav väärtus võib võrdse tõenäosusega asuda ükskõik millises massiivi elemendis.
Seega, tõenäosusega 1/n leiame otsitava väärtuse elemendist a1 juba pärast 1. võrdlust, tõenäosusega 1/n elemendist a2 pärast 2. võrdlust, ..., tõenäosusega 1/n elemendist an pärast n. võrdlust. Selle eelduse kohaselt kulub M otsingu peale kokku
|
1 + |
|
2 + ... + |
|
n =
|
|
(1 + 2 + ... + n) =
|
|
|
|
=
M |
|
Lineaarse otsingu suur ajakulu on tingitud eeskätt sellest, et iga võrdluse alusel saame edasise vaatluse alt välja jätta ainult ühe elemendi --- selle, mida me just otsitava väärtusega võrdlesime.
Kui on teada, et massiiivi elemendid on järjestatud, saame elemente kõrvale heita suuremate gruppidena. (Edasises eeldame, et massiivi elemendid on järjestatud mittekahanevalt: " i < n : ai £ ai+1. Muidugi oleks arutelu sarnane ka vastupidiselt järjestatud massiivi korral.)
Sellises massiivis saame elemendi ak otsitava väärtusega võrdlemise tulemusest teha järeldusi ka teiste elementide kohta. Tõepoolest, kui ak < x, võime edasise vaatluse alt välja jätta mitte ainult ak, vaid ka kõik ai, kus i < k, sest ükski neist ei saa olla suurem kui ak (joonis 7.2, vasakpoolne looksulg). Analoogiliselt, kui ak > x, võime edasise vaatluse alt välja jätta ka kõik ai, kus i > k (joonis 7.2, parempoolne looksulg).
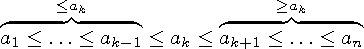
Joonis 7.2: Kahendotsimise põhiidee
Nüüd jääb veel valida k väärtus, mis annaks maksimaalse võidu. Osutub, et kasulik on igal sammul valida veel vaatluse all olevatest elementidest keskmine --- sellisel juhul saame iga võrdluse järel heita kõrvale pooled elemendid. Seda algoritmi nimetatakse kahendotsinguks (ingl binary search).
Kahendotsingu ajalise keerukuse hindamiseks võime selle sõnastada rekursiivselt: igal sammul jätame konstantse ajaga operatsiooni (ühe võrdlustehte) põhjal vaatluse alt välja pooled andmed ja jätkame sama algoritmi abil otsimist ülejäänud poolest. Selline sõnastus annab kahendotsingu ajakulu hinnanguks rekurrentse võrrandi
T(n) = Q(1) + T(n/2),
millest (eelmises peatükis toodud tabeli põhjal) saame
T(n) = Q(logn).
See tulemus näitab küll, et kahendotsing on lineaarsest oluliselt efektiivsem, kuid ei selgita, miks on kasulik just keskmine element valida.
Asi on selles, et mõne muu elemendi valimisel parandame ajahinnangut parima võimaliku juhu jaoks (näiteks, valides massiivi alguse poole jääva elemendi, saame ak > x korral kõrvale heita rohkem kui pooled elemendid), aga samal ajal halvendame seda halvima võimaliku juhu jaoks (tulemuse ak < x korral saame kõrvale heita vähem elemente). Samas, jagades massiivi ebavõrdse pikkusega osadeks, on suurem tõenäosus, et otsitav element jääb suuremasse poolde --- mis aga on meie algoritmi seisukohalt halvem võimalus.
Massiivi jagamisel võrdseteks osadeks on seega kaks kasulikku omadust: see vähendab esiteks halvema võimaluse tõenäosust ja teiseks ka halvema võimaluse halbust (tõsi küll, seda viimast parema võimaluse headuse arvelt).
Muide, massiivi ebavõrdse jagamise äärmuslikul juhul --- kui valime alati kõige vasakpoolsema elemendi --- jõuame tagasi lineaarse otsingu juurde.
Enne algoritmi detailset koostamist on kasulik mõelda ka, mida peaks tegema, kui otsitav väärtus esineb massiivis korduvalt, ja mida siis, kui seda massiivis üldse pole. Järgnev algoritm lahendab need küsimused nii: ta leiab otsitava väärtuse vasakpoolseima võimaliku pistekoha (ingl insertion point) --- see tähendab vasakpoolseima koha, kuhu me võiks selle väärtuse massiivi olemasolevate elementide vahele pista nii, et tulemuseks oleks ikkagi järjestatud massiiv.
Algoritm 2
KahOtsV: Kahendotsing massiivis
Sisend: a1 ... n --- antud massiiv, " i < n : ai £ ai+1; x --- otsitav väärtus
Väljund: tagastab x vasakpoolseima pistekoha
Abimuutujad: v, p Î N --- uuritava lõigu otspunktid;
k Î N --- lõigu keskpunkt
-
v¬1; p¬v + n
-
senikui v < p
-
--- invariant: otsitav pistekoht on v ... p
-
k¬ë(v + p) / 2û
-
kui ak < x
-
v¬k + 1
-
muidu
-
p¬k
-
lõppkui
-
lõppsenikui
-
--- vahetingimus: otsitav pistekoht on v ... p ja v = p
-
tagasta v
Väärib märkimist, et algoritmi real 4 on oluline ümardada allapoole. (Miks? Mõelge, mis juhtuks ülespoole ümardades, kui x > an.)
7.2.2 Mäluhaldus
Enne järgmise struktuuri --- lihtahela --- juurde asumist peame korraks pöörduma tagasi juba käsitletud teema juurde ja uurima dünaamiliste muutujate loomise ja kasutamise tehnikaid.
Nagu juba varem öeldud, luuakse dünaamiline muutuja programmi töö ajal vastava käsu peale. Kuna sellist muutujat ei deklareerita programmi kirjutamise ajal, pole sellel ka nime, vaid ainult aadress. Selleks, et neid muutujaid oleks siiski võimalik kasutada, on olemas spetsiaalsed andmetüübid aadresside hoidmiseks, mida nimetatakse viidatüübiks (ingl pointer) või viitetüübiks (ingl reference).
Viida- või viitetüüpi muutuja on üldiselt muutuja nagu iga teinegi, ainult tema väärtus on mäluaadress ja põhiline operatsioon selle aadressi järgi vastava mälupesa poole pöördumine.
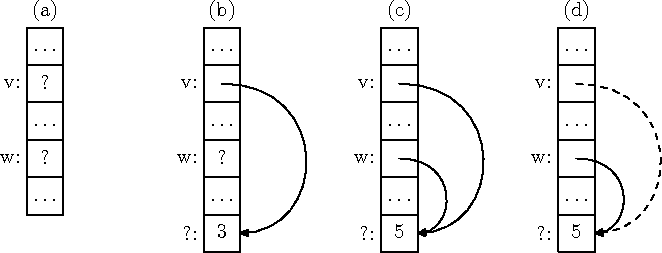
Oletame, et meil on programmis täisarvmuutuja a ja viitmuutuja v. Programmi käivitamisel eraldatakse kummalegi neist üks mälupesa, mille sisuks on üldiselt mingi juhuslik väärtus (joonis 7.3 (a)). ``Tavalisele'' muutujale väärtuse omistamisega oleme me juba tuttavad, näiteks
a¬3
salvestatab muutuja a mälupessa väärtuse 3 (joonis 7.3 (b), üleval).
Kuna viitmuutuja väärtus on aadress, siis on viitmuutujaga seotud kaks võimalikku vasakväärtust: esiteks viitmuutuja enda aadress (tema väärtuse hoidmiseks kasutatava mälupesa number) ja teiseks tema väärtus (aadress, mille hoidmiseks seda muutujat kasutatakse). Seega on viitmuutujale omistamisel vaja eristada, kumba kahest võimalikust vasakväärtusest me kasutame.
Enamasti tähendab tavaline omistamine viitmuutuja väärtuseks uue aadressi määramist, näiteks
v¬tee-uus Z
eraldab täisarvu hoidmiseks sobiva mälupesa (tee-uus Z) ja salvestatab selle mälupesa aadressi muutujasse v (joonis 7.3 (b), all). Kuna uuel muutujal ei ole nime, on seda võimalik kasutada ainult tema aadressi kaudu. Selleks on viitmuutujale omistamisel tavaliselt olemas eriline süntaks, mis näitab, et me soovime salvestada uut väärtust mitte muutuja enda mälupessa (joonisel tähistatud ``v:''), vaid tema poolt viidatavasse mälupessa (joonisel tähistatud ``?:''). Näiteks
[[v]]¬3
salvestatab v poolt viidatavasse mälupessa väärtuse 3 (joonis 7.3 (c)).
Vahel on kasulik viitmuutujasse salvestada ka mõne ``tavalise'' muutuja aadress. Selle võimaldamiseks on paljudes keeltes olemas spetsiaalne operatsioon mistahes muutuja mäluaadressi leidmiseks. Näiteks
v¬]]a[[
salvestatab muutuja a aadressi muutuja v mälupessa (joonis 7.3 (d)).
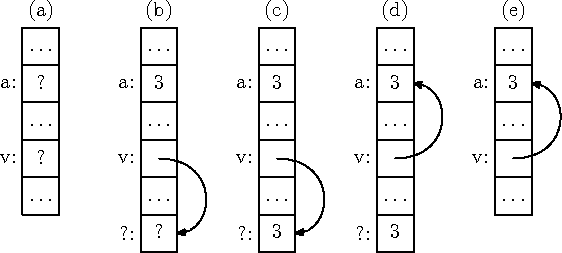
Joonis 7.3: Arv- ja viitmuutuja
Viitmuutujate kasutamisel peab silmas pidama, et me ei kaotaks ära ainukest võimalust oma dünaamilise muutuja poole pöördumiseks. Näiteks eelpool vaadeldud omistamistest koosneva programmilõigu
--- vahetingimus: joonis 7.3 (a)
a¬3
v¬tee-uus Z
--- vahetingimus: joonis 7.3 (b)
[[v]]¬3
--- vahetingimus: joonis 7.3 (c)
v¬]]a[[
--- vahetingimus: joonis 7.3 (d)
täitmise järel on meil mälus dünaamiliselt loodud täisarvmuutuja, mille poole me ei saa pöörduda, sest meil pole kuskil alles selle muutuja aadressi. Samas on see mälu hõivatud ja süsteem ei saa seda kasutada ka muude andmete hoidmiseks. Tegemist on sageli esineva programmiveaga, mida nimetatakse mälulekkeks (ingl memory leak).
Mälulekete vältimiseks kasutatakse paljudes kõrgkeeltes prahikoristust (ingl garbage collection) --- süsteem kustutab automaatselt kõik dünaamilised muutujad, millele ei osuta enam ükski viit.
Keeltes, kus prahikoristust ei ole, tuleb mittevajalikud dünaamilised muutujad kustutada spetsiaalse käsu abil. Näiteks programmilõik
--- vahetingimus: joonis 7.3 (a)
a¬3
v¬tee-uus Z
--- vahetingimus: joonis 7.3 (b)
[[v]]¬3
--- vahetingimus: joonis 7.3 (c)
kustuta v
v¬]]a[[
--- vahetingimus: joonis 7.3 (e)
mälu ei lekita, kuna dünaamiline muutuja kustutatakse mälust enne selle aadressi ``unustamist''.
Muutujate mälust kustutamisel kehtivad järgmised reeglid:
-
Kustutada tohib ainult dünaamilisi muutujaid. Selle reegli vastu on kerge eksida, kui programmis kasutatakse viitu, mis osutavad staatilistele või automaatsetele muutujatele.
- Iga muutuja tuleb kustutada täpselt üks kord. Eelpool juba oli näide mälulekke kohta, mis tekib, kui dünaamilist muutujat üldse ei kustutata. Muutuja korduv kustutamine on isegi raskem viga, sest võib ajada segadusse süsteemi arvepidamise vaba ja kasutatud mälu üle. Selle reegli vastu on kerge eksida, kui ühele muutujale osutab mitu viita.
- Kustutatud muutujat enam kasutada ei tohi. Ka selle reegli vastu on eriti kerge eksida, kui ühele muutujale osutab mitu viita.
Mitut viita, mis osutavad samale muutujale, nimetatakse teisikuteks (ingl alias). Teisikviitade ja nendega seotud probleemide illustratsiooniks vaatleme joonist 7.4 ja paneme programmilõigu
--- vahetingimus: joonis 7.4 (a)
v¬tee-uus Z
[[v]]¬3
--- vahetingimus: joonis 7.4 (b)
w¬v
[[w]]¬5
--- vahetingimus: joonis 7.4 (c)
kustuta v
--- vahetingimus: joonis 7.4 (d)
kohta tähele järgmist:
-
Omistamine [[w]]¬... muudab lisaks [[w]] väärtusele ka [[v]] väärtust. See on muidugi ootuspärane, arvestades, et [[w]] ja [[v]] on tegelikult üks muutuja. Küll aga tuleb see üllatusena, kui programmeerija ei märka, et v ja w on teisikud.
- Samal põhjusel ei tarvitse pärast dünaamilise muutuja kustutamist v kaudu olla ilmne, et kadunud on ka w poolt viidatav muutuja. Kui süsteem pole vabanenud mäluosa millegi muu jaoks kasutusele võtnud, võib [[w]] kasutamine pärast muutuja kustutamist isegi õnneks minna. See on eriti ohtlik, sest sellisel juhul võib viga programmi testimisel märkamata jääda ja avalduda alles selle reaalsel kasutamisel.
- Paljudes keeltes pole eelmise vea tegemiseks teisikuid vajagi, sest ka v säilitab oma väärtuse ja ka selle kaudu on võimalik püüda kustutatud muutuja poole pöörduda. Tagajärjed on muidugi samad, ainus erinevus on selles, et niisugust viga on kergem märgata (ja seega tegemata jätta). Ka aitab vea seda juhtu ära hoida muutujale v tühiviida omistamine kohe pärast käsku kustuta v.
Tühiviit on spetsiaalne viidatüüpi väärtus, millele ei vasta reaalset mäluaadressi. Enamikus süsteemides toob iga katse tühiviida poolt osutatava mälupesa poole pöörduda kaasa veaolukorra, mistõttu see ei jää programmi testimisel märkamata. Tühiviita tähistatakse erinevates keeltes erinevalt1, meie kasutame edaspidi sümbolit ^.
Joonis 7.4: Teisikviidad
Muidugi oleks kõiki neid vigu võimalik vältida, kui süsteem kontrolliks iga kustutamiskäsu juures vabastatava aadressi olekut ja nulliks kõik sellele muutujale osutavad viidad. Paraku oleks see väga ressursikulukas, mistõttu seda ei tehta. Seega peab programmeerija ise hoolikas olema.
Nagu lubatud, vaatleme järgmise andmestruktuurina lihtahelat.
Lihtahel (ingl singly linked list) koosneb elementidest, millest igaühes on lisaks rakenduse seisukohalt vajalikele andmetele ka järgmise elemendi aadress. Nii on ahela töötlemisel võimalik liikuda esimeselt elemendilt teisele, teiselt kolmandale ja nii edasi kuni ahela lõpuni. Ahela viimases elemendis on tühiviit, mis annabki märku ahela lõpust.
Tavaliselt kasutatakse ahela hoidmiseks viita selle esimesele elemendile. Rohkem pole vaja, sest esimeselt elemendilt saame liikuda kõigi teisteni.
Ahelat kui andmestruktuuri iseloomustavad järgmised omadused:
-
Ahela pikkus ei ole fikseeritud. See võimaldab ahela abil realiseerida muutuva suurusega andmestruktuure ka keeltes, kus massiivi pikkus tuleb määrata juba programmi kirjutamise ajal.
- Ahela elemendi leidmine tema indeksi järgi on üsna kulukas. Üldjuhul tuleb selleks alustada ahela algusest ja liikuda vastav arv kordi ühelt elemendilt teisele. Seega on i. elemendi leidmise ajakulu Q(i).
- Ahela elemendi väärtuse väljavahetamine (ahela elemendi andmeväljale uue väärtuse omistamine) on tavaline omistamistehe ja selleks tehtava töö maht (kui element on juba leitud) ei sõltu ei ahela pikkusest ega elemendi positsioonist ahelas.
- Uue elemendi lisamine ahelasse on üldiselt efektiivne operatsioon. Kui meil on olemas lisamispositsioonile eelneva elemendi aadress, kulub lisamiseks ainult kaks viitmuutuja omistamist (joonis 7.5).
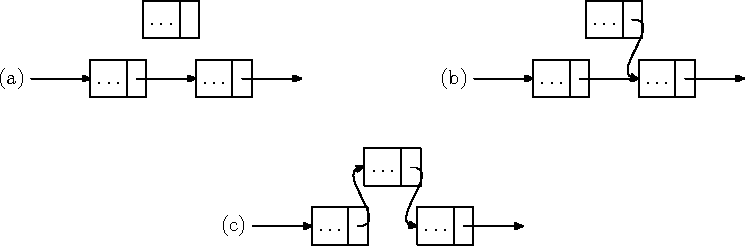
Joonis 7.5: Elemendi lisamine ahelasse
Täpselt sama efektiivne on ühe elemendi asemel terve teise ahela lisamine ahelasse, kui meil on (lisaks lisamispositsioonile eelneva elemendi aadressile) olemas lisatava ahela esimese ja viimase elemendi aadressid.
- Ahelast elemendi eemaldamine on üldiselt efektiivne operatsioon. Kui meil on olemas eemaldatavale elemendile eelneva elemendi aadress, kulub eemaldamiseks ainult üks viitmuutuja omistamine (joonis 7.6).
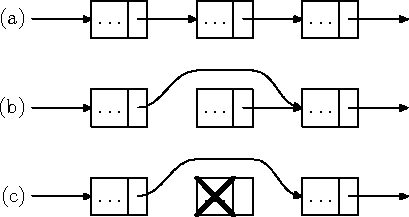
Joonis 7.6: Elemendi eemaldamine ahelast
Sama efektiivne on ühe elemendi asemel terve lõigu eemaldamine ahelast, kui meil on (lisaks eemaldamispositsioonile eelneva elemendi aadressile) olemas eemaldatava lõigu viimase elemendi aadress.
Muidugi tuleb mõlemal juhul arvestada lisaks ka eemaldatud elementide mälust kustutamisega.
Nagu eelnevast näha, on ahela kasutamisel sageli vaja jooksvale elemendile eelneva elemendi aadressi. See tekitab raskusi ahela esimese elemendi töötlemisel, sest sellele eelnev element puudub.
Tihti on mugavaim lahendus lisada ahela algusse fiktiivne element, mille andmeväljad on tühjad ja mille ainus ülesanne on olla esimesele tegelikule elemendile eelnev element. Sellist ahelat nimetatakse päisega lihtahelaks ja lisatud elementi päiseelemendiks ehk päiseks (ingl header).
Teine komplikatsioon lihtahela kasutamisel on, et antud elemendile eelneva elemendi leidmine on üsna kulukas operatsioon. Üldjuhul tuleb selleks alustada ahela algusest ja liikuda edasi, kuni jõuame otsitava elemendini.
Paljudes algoritmides on võimalik ahela läbimiseks kasutada kaht muutujat, millest üks osutab eelmisele ja teine jooksvale elemendile. Sellist paari nimetatakse tandemiks.
Kui algoritmi pole siiski võimalik (või efektiivne) üles ehitada tandemile, võib lihtahela asemel kasutada topeltahelat (ingl doubly linked list), mille igas elemendis on lisaks andmeväljadele kaks viita: üks eelmisele, teine järgmisele elemendile.
Topeltahela peamine halvemus lihtahelaga võrreldes on keerukam viitade süsteem ja sellest tulenevalt ka keerukamad lisamis- ja eemaldamisoperatsioonid. Muidugi võib ka topeltahelast teha päisega variandi.
Kuna kõigis neis ahelates on indeksi järgi elemendi leidmine ikkagi kulukas, on väärtuse järgi elemendi leidmiseks mõeldav ainult lineaarne otsimine. Ahelas, erinevalt massiivist, oleks kahendotsimine lineaarsest aeglasem.
7.3 Järjestamine
Massiiv ja ahel on esitatavad elementide loendina ja sellest tekib tihti vajadus loetleda nende elemente nende väärtuste järjekorras. Andmeid võib järjestada (ingl order) ehk sortida (ingl sort) paljude erinevate algoritmide abil.
Korduslausete peatükis vaatlesime ühe näitealgoritmina pistemeetodit (ingl insertion sort):
Algoritm 3
PisteSort
Sisend: a1 ... n --- töödeldav massiiv
Väljund: a1 ... n --- väärtused vahetatud nii, et " i < n : ai £ ai+1
Abimuutujad: i, j
-
korda i¬1 ... n
-
--- invariant: a1 £ a2 £ ... £ ai-1
-
j¬i
-
senikui j > 1
-
--- invariant: aj £ aj+1 £ ... £ ai
-
kui aj-1 > aj
-
aj-1«aj
-
j¬j-1
-
muidu
-
j¬1
-
lõppkui
-
lõppsenikui
-
lõppkorda
Olles vahepeal läbinud keerukuse peatüki võime nüüd hinnata ka selle algoritmi efektiivsust. Selleks paneme tähele, et sisemise korduslause kehaks on meil tingimuslause, milles on üks võrdlemine ja (sõltuvalt võrdluse tulemusest) üks või neli omistamist. Igal juhul on selle korduse keha täitmiseks kuluv aega tõkestatud mingi massiivi suurusest sõltumatu konstandiga. Seega on sisemise korduse keha keerukus Q(1).
Seda kordust võidakse läbida minimaalselt 1 kord (kui ai on a1..i hulgas maksimaalne) ja maksimaalselt i korda (kui ai on a1..i hulgas vähim). Kui massiiv on alguses järjestatud juhuslikult, võiks eeldada, et elemendi ai lõpliku asukohana on võrdtõenäolised kõik i erinevat positsiooni, mis annab sisemise korduse täitmiste keskmiseks arvuks i/2.
Välimist kordust läbitakse täpselt n korda, mis annab kogu algoritmi keerukuseks parimal, halvimal ja keskmisel juhul vastvalt
|
|
| Tmin(n) |
= |
|
|
| Tmax(n) |
= |
|
|
| T(n) |
= |
|
|
|
Pistemeetodit on võimalik kohandada lihtahela sortimiseks. Kuna lihtahelas on võimalik liikuda ainult ühes suunas, tuleb sel juhul ka sisemises korduses liikuda ahela alguse poolt lõpu poole. See muudab küll algoritmi vahetingimusi, kuid mitte selle efektiivsust.
Korduslausete peatükist on tuttav ka teine suhteliselt lihtne sortimisalgoritm, valikumeetod (ingl selection sort):
Algoritm 4
ValikuSort
Sisend: a1 ... n --- töödeldav massiiv
Väljund: a1 ... n --- väärtused vahetatud nii, et " i < n : ai £ ai+1
Abimuutujad: i, j, k
-
korda i¬1 ... n
-
--- invariant: a1 £ a2 £ ... £ ai-1
-
--- invariant: " j ³ i : aj ³ ai-1
-
k¬i
-
korda j¬i + 1 ... n
-
--- invariant: ak = min(ai ... j - 1)
-
kui aj < ak
-
k¬j
-
lõppkui
-
--- vahetingimus: ak = min(ai ... j)
-
lõppkorda
-
--- vahetingimus: ak = min(ai ... n)
-
ai«ak
-
--- vahetingimus: " j ³ i : aj ³ ai
-
--- vahetingimus: a1 £ a2 £ ... £ ai
-
lõppkorda
Ajalise keerukuse hindamine on seekord isegi lihtsam kui pistemeetodi puhul: sisemise korduse keha on Q(1); sisemist kordust läbitakse n - i korda ja välimist n korda, mis kokku annab selle meetodi keerukuseks igal juhul
|
|
| T(n) |
= |
|
|
| |
= |
| (n 2 - |
|
) Q(1) = |
|
Q(1) = Q(n2).
|
|
|
|
Valikumeetodi puhul on Q(n2) ainult elementide võrdlemiste arv, järjestatava massiivi elementide omistamiste arv on Q(n), mis võib olla oluline, kui elemendid on suured kirjed või kui nende liigutamisega kaasneb mingeid muid kulutusi (näiteks võivad mingid teised andmestruktuurid hoida elementide indekseid, mida tuleks elemendi liigutamisel uuendada).
Valikumeetod vajab töödeldavate andmete hulgas ainult ühesuunalist liikumist (mõlemad kordused liiguvad andmete alguse poolt lõpu poole), seega on see peaaegu muutusteta kasutatav ka lihtahela sortimiseks.
Praktikas on massiivide sortimisel üldiselt efektiivseim kiirmeetod (ingl quicksort). Selle meetodi põhiidee jagada massiiv a1 ... n kaheks osaks a1 ... k ja ak+1 ... n nii, et ükski esimese osa element pole suurem ühestki teise osa elemendist (joonis 7.7, üleval). Pärast seda võime kummagi osa eraldi sortida ja saamegi tulemuseks korrektselt järjestatud massiivi.
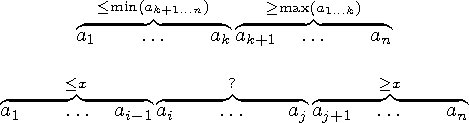
Joonis 7.7: Kiirmeetodi põhiidee
Jaotamiseks valime mingi massiivis esineva väärtuse x ning hakkame sellest väiksemaid elemente koguma massiivi esimesse ja suuremaid teise poolde (joonis 7.7, all). Alustame seisust i = 1, j = n ning liigume edasi i¬i+1, kui ai < x (see tähendab, kui ai kuulub esimesse poolde) ja j¬j-1, kui aj > x (kui aj kuulub teise poolde). Kui oleme mõlemas pooles avastanud elemendi, mis võiks kuuluda vastaspoolde, vahetame need elemendid omavahel ja jätkame võrdlemist kuni vaatlemata osa ai ... j on tühi.
Kui kasutada kummagi jaotamisel saadud massiiviosa sortimiseks sama meetodit, on tulemuseks järgmine rekursiivne algoritm:
Algoritm 5
KiirSort
Sisend: av ... p --- töödeldav massiiviosa
Väljund: av ... p --- väärtused vahetatud nii, et av £ ... £ ap
Abimuutujad: i, j, x
-
kui v < p
-
i¬v; j¬p
-
x¬aë(i+j)/2û
-
senikui i < j
-
--- invariant: " i' < i : ai' £ x ja " j' > j : aj' ³ x
-
senikui ai < x
-
--- invariant: " i' < i : ai' £ x
-
i¬i + 1
-
lõppsenikui
-
senikui aj > x
-
--- invariant: " j' > j : aj' ³ x
-
j¬j - 1
-
lõppsenikui
-
kui i < j
-
ai«aj
-
i¬i + 1; j¬j - 1
-
lõppkui
-
lõppsenikui
-
KiirSort(av ... j)
-
KiirSort(aj+1 ... p)
-
muidu
-
--- ühest elemendist koosnev osa on alati sorditud
-
lõppkui
Kiirmeetodi ajalise keerukuse hindamiseks paneme tähele, et n-elemendilise massiivi jagamiseks kulub igal juhul Q(n) sammu, millele järgneb kaks rekursiivset väljakutset.
Parimal juhul õnnestub massiiv igal sammul jagada kaheks võrdseks osaks. Siis on kiirmeetodi keerukus
Tmin(n) = Q(n) + 2 Tmin(n/2) = Q(n logn).
Halvimal juhul valime ``veelahkmeks'' alati kas maksimaalse või minimaalse väärtusega elemendi ja saame tulemuseks jaotuse 1- ja (n-1)-elemendiliseks osaks. Siis on kiirmeetodi keerukus
Tmax(n) = Q(n) + Tmax(n-1) = Q(n2).
Õnneks realiseerub halvim stsenaarium üliharva ja keskmiselt on kiirmeetodi ajaline keerukus optimistlik T(n) = Q(n logn). Selle tulemuse tõestamine pole aga sugugi triviaalne ja jääb siinkohal tegemata.
Kuna kiirmeetod vajab kindlasti kahesuunalist liikumist andmete hulgas, ei sobi ta lihtahela töötlemiseks. Küll aga on võimalik seda algoritmi kohandada kasutamiseks topeltahelal.
Lisaks senivaadelduile on olemas veel palju huvitavaid sortimisalgoritme, millega tasuks kindlasti tutvuda peatüki lõpus soovitatud raamatute abil.
7.4 Abstraktsemad struktuurid
Magasin (ingl stack) ehk pinu on lineaarne andmestruktuur, mis võimaldab juurdepääsu oma elementidele kindlas järjekorras --- magasinist elemendi väljavõtmisel saame esimesena selle elemendi, mille me sinna viimasena panime, järgmisena selle, mille panime eelviimasena jne.
Sellise juurdepääsusüsteemi kohta kasutatakse sageli lühendit LIFO (ingl last-in-first-out) ja seda võib kujutleda ühest otsast kinnise toruna (joonis 7.8) --- mistahes elemendi kättesaamiseks peame kõigepealt eest ära võtma need, mis on tema ja toru lahtise otsa vahel.
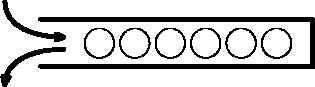
Joonis 7.8: Magasini tööpõhimõte
Põgusalt puutusime magasini mõistega kokku juba alamprogramme käsitledes. Seda meenutades on selge, et alamprogrammide aktiveerimiskirjete hoidmiseks on kõige õigem just magasin --- kui üks alamprogramm kutsub välja teise ja teine omakorda kolmanda, tahame loomulikult, et kolmanda alamprogrammi töö lõppedes jätkatakse teise alamprogrammi täitmist ning esimese juurde pöördutakse tagasi alles pärast teise lõpetamist.
Kuna LIFO-tüüpi andmehoidla on kasulik ka mitmetel muudel juhtudel, tuleb keeltes, kus magasinitüüpi standardselt olemas ei ole, see realiseerida mõne teise andmestruktuuri abil.
Üks võimalus on kasutada magasini baasina massiivi. See on üsna lihtne: hoiame magasini elementide arvu muutujas n ja magasini sisu massiivi a elementides a1 kuni an nii, et an on kõige uuem element (joonis 7.9). Andmete magasini panemisel suurendame n väärtust ja salvestame uued andmed massiivi elementi an. Andmete magasinist võtmisel tagastame an sisu ja seejärel vähendame n väärtust.

Joonis 7.9: Magasin massiivi baasil
Alternatiiv on kasutada lihtahelat (joonis 7.10). Ka see pole palju keerulisem, kui hoiame magasini sisu ahelas nii, et uuemad elemendid on ahelas vanematest eespool. Andmete magasini panemisel lisame uusi kirjeid ahela algusse, andmete võtmisel tagastame ahela esimese elemendi sisu. Kõik lisamise ja eemaldamise operatsioonid toimuvad alati ahela alguses, mis on juurdepääsu efektiivsuse seisukohalt parim variant.
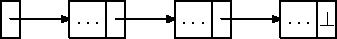
Joonis 7.10: Magasin lihtahela baasil
Teine lihtne, aga kasulik andmestruktuur on järjekord (ingl queue). Ka järjekord võimaldab juurdepääsu oma elementidele kindlas järjekorras, kuid erinevalt magasinist tagastab järjekord esimesena oma vanima elemendi.
Sellise juurdepääsusüsteemi kohta öeldakse FIFO (ingl first-in-first-out) ja seda võib kujutleda toruna, mille sisu liigub alati ühes suunas (joonisel 7.11 vasakult paremale).
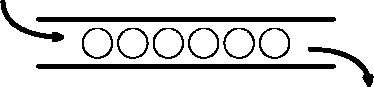
Joonis 7.11: Järjekorra tööpõhimõte
Järjekord on kasulik sellistes algoritmides, kus mingi protsess toodab andmeid ja mingi teine protsess tarbib neid, aga pole garanteeritud, et tarbija kõige toodetuga piisavalt kiiresti hakkama saab. Väga levinud on sellised ``torud'' multitegumsüsteemides, aga peagi näeme, et neist võib olla kasu isegi siis, kui andmete tootja on ise ka nende tarbija.
Ka järjekorra võib realiseerida massiivi baasil, kuid efektiivse tulemuse saamine on sel juhul natuke keerulisem. Magasinis toimus andmete lisamine ja eemaldamine elementide jada samas otsas, jada teine ots ``püsis paigal''. Järjekorra puhul see aga nii ei ole. Püüd hoida järjekorra elemente alati massiivi ühes otsas tähendaks seda, et üks kahest operatsioonist (lisamine või eemaldamine) nõuaks kõigi elementide nihutamist.
Selle vältmiseks on kasulikum hoida eraldi järjekorras olevate elementide arvu n ja esimese elemendi indeksit e. Järjekorra elemendid on sellisel juhul massiivi a elementides ae, ae+1, ..., ae+n-1. Esimene vaba element on ae+n. Selleks, et indeksid järjekorra kasutamisel tõkestamatult kasvama ei hakkaks, kasutame massiivi ringpuhvrina, kus massiivi viimasele elemendile järgneb esimene (joonis 7.12). Selline lahendus võimaldab realiseerida nii lisamise kui eemaldamise massiivi suurusest või järjekorras olevate elementide arvust sõltumatu väikese ajakuluga.
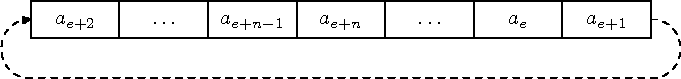
Joonis 7.12: Järjekord massiivi baasil
Vajadus pääseda kiiresti ligi järjekorra mõlemale otsale komplitseerib ka selle realiseerimist lihtahela baasil. Siin on lahenduseks hoida eraldi viita järjekorda kujutava ahela viimasele elemendile (joonis 7.13). Erinevalt igapäevase elu elavast järjekorrast, kus inimene jätab meelde tema ees seisja, on arvutis kasulikum hoida igas elemendis talle järgneva aadressi. Seega on lihtahela alguses järjekorra vanim ja lõpus uusim element.
Järjekorra viimase elemendi eemaldamisel tuleb panna tähele, et meil on tegemist teisikviitadega: kuna ainus element on ahelas üheaegselt nii esimene kui ka viimane, osutavad mõlemad viidad talle ja elemendi eemaldamisel tuleks ka mõlemad nullida.
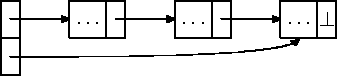
Joonis 7.13: Järjekord lihtahela baasil
Ülesanded
Ülesanne 1
Kui otsitav väärtus esineb massiivi elementide hulgas korduvalt, leiab LinOtsV selle vasakpoolseima (vähima indeksiga) esinemiskoha. Kirjutada LinOtsP, mis leiab otsitava väärtuse parempoolseima (suurima indeksiga) esinemiskoha. Tuua välja selle korduse invariant.
Ülesanne 2
KahOtsV leiab antud väärtuse jaoks vasakpoolseima võimaliku pistekoha. Kirjutada KahOtsP, mis leiab parempoolseima võimaliku pistekoha. Tuua välja selle korduse invariant ja põhjendada selle säilimist korduse keha täitmisel.
Ülesanne 3
Realiseerida lihtahela jaoks lineaarse otsimise mõlemad variandid (nii LinOtsV kui ka LinOtsP analoog).
Ülesanne 4
Koostada algoritmid päisega topeltahela elementide lisamiseks ja eemaldamiseks.
Lisamisoperatsiooni parameetrid on lisamispositsioonile eelneva elemendi aadress ja lisatava elemendi aadress. Eemaldamisoperatsiooni ainus parameeter on eemaldatava elemendi aadress.
Kontrollida, et mõlemad operatsioonid töötavad õigesti ka ahela esimese ja viimase elemendi lisamisel ja eemaldamisel.
Ülesanne 5
Realiseerida algoritm PisteSort lihtahela jaoks.
Kirjandus
- Rein Jürgenson. Andmestruktuuride lühikursus. Tallinna Tehnikaülikool, 2000.
- Põhilisi andmestruktuure ja nende realiseerimist käsitlev õpik algajatele. 96 lk.
- Jüri Kiho. Algoritmid ja andmestruktuurid. Tartu Ülikool, 2003.
- Andmestruktuuride ja põhialgoritmide õpik. 148 lk.
- Robert Sedgewick. Algorithms. Addison-Wesley, 1988.
- Klassikaline andmestruktuuride ja algoritmide õpik. 650 lk. Osutatud väljaandes on programminäited toodud Pascalis, hiljem on ilmunud ka Algorithms in C, Algorithms in C++ ja Algorithms in Java.
- Thomas H. Cormen, Clifford Stein, Charles Leiserson, Ronald Rivest. Introduction to Algorithms. MIT, 2001.
- Eelmise trükiga klassikaks saanud algoritmide ja andmestruktuuride põhiõpik, de facto standard paljudes ülikoolides üle maailma. 1180 lk.
- Томас Кормен, Чарльз Лейзерсон, Рональд Ривест. Алгоритмы: построение и анализ. МЦНМО, 2001.
- Eelmise tõlge. 960 lk.
- Sanjoy Dasgupta, Christos H. Papadimitriou, Umesh V. Vazirani. Algorithms. McGraw-Hill, 2006.
- Berkeley ja UCSD algoritmide ja andmestruktuuride kursuste põhjal koostatud õpik, sobib väga hästi ka iseseisvaks õppimiseks. 336 lk.
Aadressil http://www.cse.ucsd.edu/users/dasgupta/mcgrawhill/ on väljas ka täistekst.
- Donald E. Knuth. The Art of Computer Programming. Addison-Wesley, 1997.
- Monumentaalne teos, mille algselt planeeritud 7 köidet pidid koondama kõik olulisemad teadmised programmeerimise ja algoritmide kohta. Väga põhjalik, aga algajale üsna raske lugemine. Seni ilmunud 3 köidet: Volume 1: Fundamental Algorithms, 670 lk; Volume 2: Seminumerical Algorithms, 776 lk; Volume 3: Sorting and Searching, 794 lk.
http://www-cs-faculty.stanford.edu/~knuth/taocp.html
- Дональд Э. Кнут. Искусство программирования. Вильямс, 2000.
- Eelmise tõlge. 720+832+844 lk.
- 1
- Näiteks Pascalis nil, Visual Basicus Nothing, C's NULL, C++'s 0, Javas null.