3.4. Paramagneetilise tsentri ionisatsioon Arrheniuse mudeli järgi parameetrite erinevate väärtuste korral.

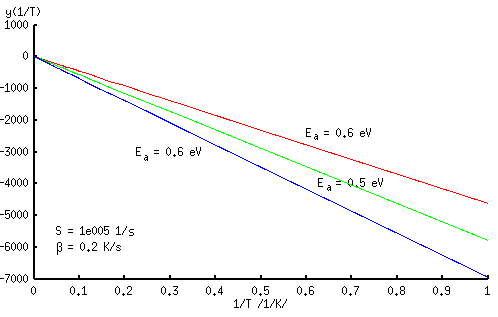
Valemist (3.2.8) on näha, et aktivatsioonienergia ja sagedusfaktor määravad üheselt kontsentratsiooni igal temperatuuril T, kui kontsentratsiooni muutumise kiirus allub valemile (3.2.5). Skaalas n(T)-T määravad nii aktivatsioonienergia kui ka sagedusfaktor protsessi asukoha temperatuuriskaalas ehk kõvera käänupunkti ja temperatuurivahemiku, mille kestel toimub kontsentratsiooni vähenemine. Skaalas dn(T)/dT-1/T määratakse vastavalt kõvera maksimum ja poollaius.

Joonis 3.4: Normeeritud kontsentratsioon N(T) erinevate aktivatsioonienergiate korral.

Joonis 3.5: Normeeritud kontsentratsiooni tuletis erinevate aktivatsioonienergiate korral.

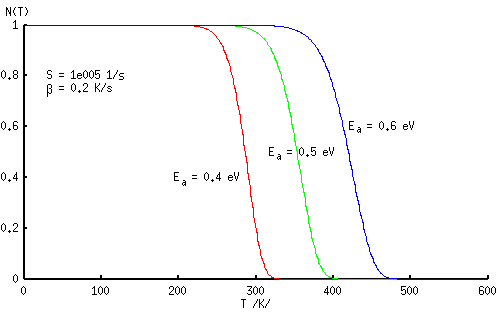
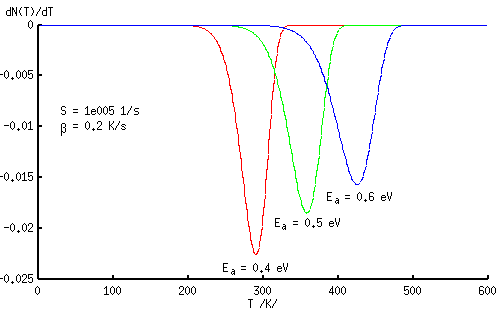
Aktivatsioonienergia suurenemisel nihkub n(T) käänupunkt kõrgemate temperatuuride poole. Sellele vastab dn(T)/dT poollaiuse suurenemine. Seega algab kontsentratsiooni märgatav vähenemine suuremate aktivatsioonienergiate korral hiljem ja kestab kauem. Aktivatsioonienergia vähenemisel nihkub protsess madalamate temperatuuride poole ja kestab kiiremini.

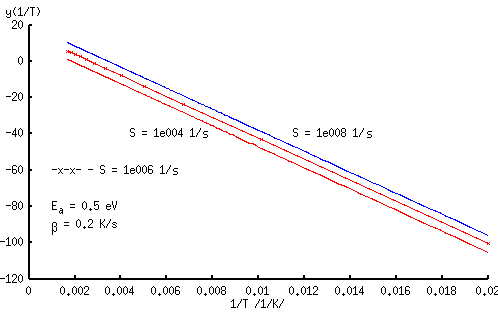
Sagedusfaktori suurenemisel nihkub n(T) käänupunkt madalamate temperatuuride poole ehk dn(T)/dT poollaius väheneb.

Joonis 3.6: Normeeritud kontsentratsioon N(T) erinevate sagedusfaktorite korral.

Joonis 3.7: Normeeritud kontsentratsiooni tuletis erinevate sagedusfaktorite korral.

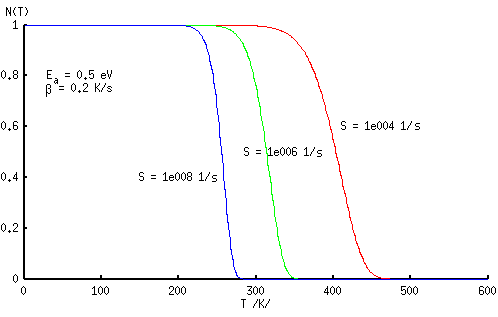
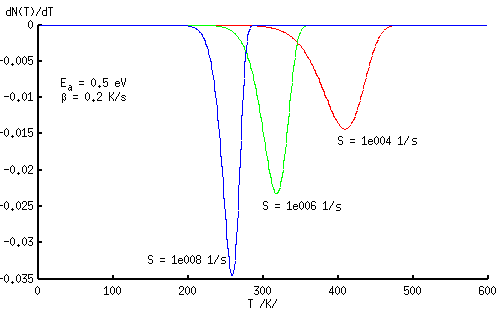
Nagu juba varem mainitud, saab sirge tõusu ja algordinaati teades valemitest (3.2.16) ja (3.2.17) üheselt määrata aktivatsioonienergia ja sagedusfaktori. Jooniselt 3.8 on võimalik veenduda, et aktivatsioonienergia muutumine tähendab sirge (3.2.15) tõusu muutumist. Sagedusfaktori muutumisel muutub sirge algordinaat ehk toimub paralleellüke. Seega vastab kindlale funktsioonile n(T) üks kindel aktivatsioonienergia väärtus ja üks kindel sagedusfaktori väärtus.

Joonis 3.8: Funktsioon y(1/T) erinevate aktivatsioonienergiate korral.

Joonis 3.9: Funktsioon y(1/T) erinevate sagedusfaktorite korral.

Üles seatud Sun., 07.11.1999.
Viimati muudetud Sun., 07.11.1999 05:27 PM CEST
WWW-lehekülje kujundus, õigused, vastutus © Heiki Kasemägi, 1999