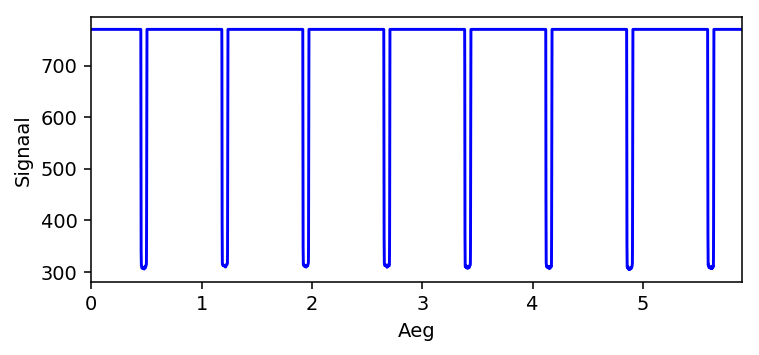
Optimaalne meetod perioodilise signaali fundamentaalsageduse (ehk perioodi) määramiseks sõltub signaali iseloomust. Esmalt vaatleme sellist olukorda, kus perioodiliselt leiab aset signaali tugevuse järsk muutus:

Algoritm on kätketud järgmisse funktsiooni, mis tagastab nii perioodi kui ka selle standardhälbe:

from scipy.stats import linregress

def leia_periood(aeg, signaal):
    signaal = signaal - 0.5 * (signaal.min() + signaal.max())
    valitud = ( signaal[:-1] > 0 ) & ( signaal[1:] < 0 )
    üleminekuhetked = aeg[:-1][valitud]
    indeks = np.arange(len(üleminekuhetked))
    T, _, _, _, ΔT = linregress(indeks, üleminekuhetked)
    return T, ΔT

Siin teostatakse järgmised sammud:

• Signaal tsentreeritakse vertikaaltelje sihis, et kõige järsemad muutused jääksid nulli ümbrusse.
• Tuvastatakse kõik sellised järjestikuste punktide paarid, kus antud punktis on positiivne signaal ja järgmises punktis juba negatiivne.
• Saadud tõeväärtusmassiivi abiga filtreeritakse välja vastavad ajahetked (toodud näidissignaali jaoks on tulemus kujutatud järgneval joonisel).
• Kui periood on konstant, siis vastavad ajahetked peavad olema lineaarses seoses oma järjekorranumbriga, st $t_i=iT +\text{Const}$. Sobitades sirge läbi vastavate andmete, saamegi kätte perioodi $T$.

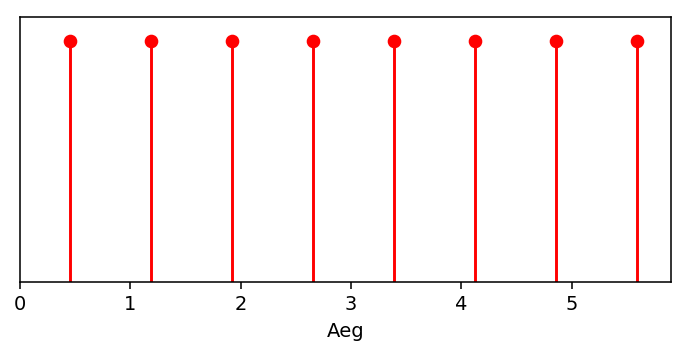
Hinnanguliselt, sellisel viisil määratud perioodi viga on ilmselt suurusjärgus $\Delta t/n$, kus $\Delta t$ on mõõtmise ajasamm ja $n$ on tuvastatud täisperioodide arv.

Järgmine levinud stsenaarium on selline, kus signaal on vähemalt ligikaudu harmooniline:

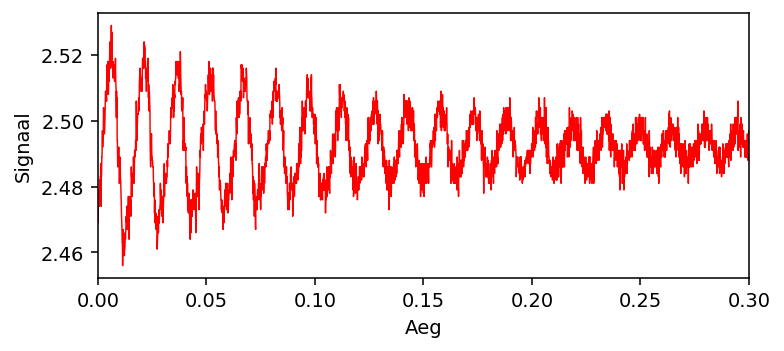
Seega mingit lõiku sellest signaalist võiks sobitada siinus- või koosinusfunktsiooniga. Ei ole ka raske modelleerida amplituudi muutumist, näiteks sumbumist või modulatsiooni. Antud signaali võiks kirjeldada järgmine funktsioon: $$f(t)=Ae^{-kt}\sin(\omega t+\phi) + b.$$ Siin vabad parameetrid on algamplituud $A$, ringsagedus $\omega$, sumbetegur $k$, algfaas $\phi$ ja kesknivoo ehk baasjoon $b$. Selliste mittelineaarsete funktsioonide sobitamiseks (vähimruutude mõttes) vajaliku algoritmi realiseerib scipy.optimize.curve_fit:

from scipy.optimize import curve_fit

# mudelfunktsioon, peab olema vektoriseeritud kujul
f = lambda t, a, k, w, phi, b: a * np.exp(-k * t) * np.sin(w * t + phi) + b

# alglähend, katse-eksituse meetodil
p = 0.036, 6, 410, -0.5, 2.495

# esialgu, alglähendi nägemiseks, kommenteerida välja
p, _ = curve_fit(f, aeg, signaal, p)

ξ = np.linspace(0, 0.3, 500)
ψ = f(ξ, *p)

figure(figsize=(6,2.5))
plot(aeg, signaal, 'r-', label='katse', lw=0.75)
plot(ξ, ψ, 'b-', label='mudel')
xlim(0, 0.3)
xlabel('Aeg')
ylabel('Signaal')
grid()
legend()
show()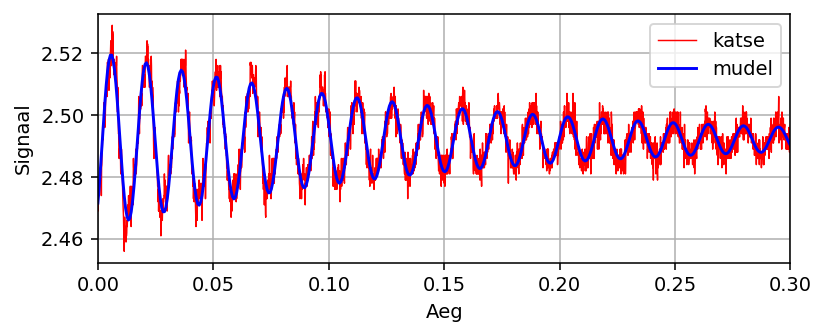

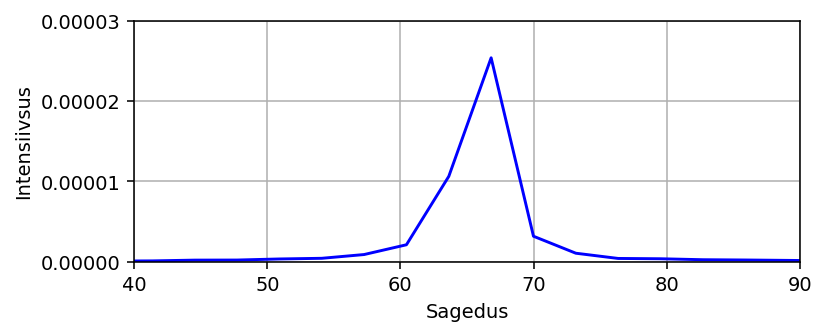
Kiire Fourier' teisenduse abiga võib ka arvutada signaali spektri tervikuna, kuigi see otseselt põhisagedust ei anna. Sellegipoolest peaks hästi näha olema sageduse nihe, kui võrrelda erinevate signaalide spektreid (või sama signaali spektreid erinevates ajavahemikes). Pikema signaali korral ongi selleks otstarbeks spetsiaalne tööriist scipy.signal.spectrogram.

def arvuta_spekter(aeg, signaal):
    n = len(aeg)
    fft = np.fft.rfft(signaal) / n
    intens = np.abs(fft)**2
    Δt = (aeg[-1] - aeg[0]) / (n - 1)  # keskmine ajasamm
    sagedus = np.fft.rfftfreq(n, Δt)
    return sagedus, intens

sagedus, intens = arvuta_spekter(aeg, signaal)

figure(figsize=(6,2.5))
plot(sagedus, intens, 'b-')
xlim(40, 90)
ylim(0, 3e-5)
xlabel('Sagedus')
ylabel('Intensiivsus')
grid()
show()

Sisukord