Sageli juhtub, et mõõteseadme lahutusvõime (ajaline, ruumiline, spektraalne, …) on sedavõrd piiratud, et signaali tegelikku kuju ei õnnestu adekvaatselt üles võtta. Järgneval joonisel on näitena temperatuurianduri signaal teatava termodünaamilise protsessi mõõtmisel. Siin on oluline piisava ajalise lahutuse saavutamine. Alghetkel ($t=0$) keskkonna temperatuur muutub hüppeliselt ja hakkab seejärel relakseeruma. Seevastu anduri signaal muutub sujuvalt (piiratud soojusvahetuskiiruse tõttu) ja algset järsku temperatuurimuutust ei ole võimalik otseselt mõõta. Otseselt andmepunktidest saadav parim hinnang algtemperatuurile on selles näites 20,9°C, kuid on ilmne, et tegelik algtemperatuur on märksa madalam. Täpsema hinnagu saamiseks tuleb kogu süsteemi (sh andurit) tõepäraselt modelleerida ja leitud mudelfunktsioon sobitada katseandmetega.

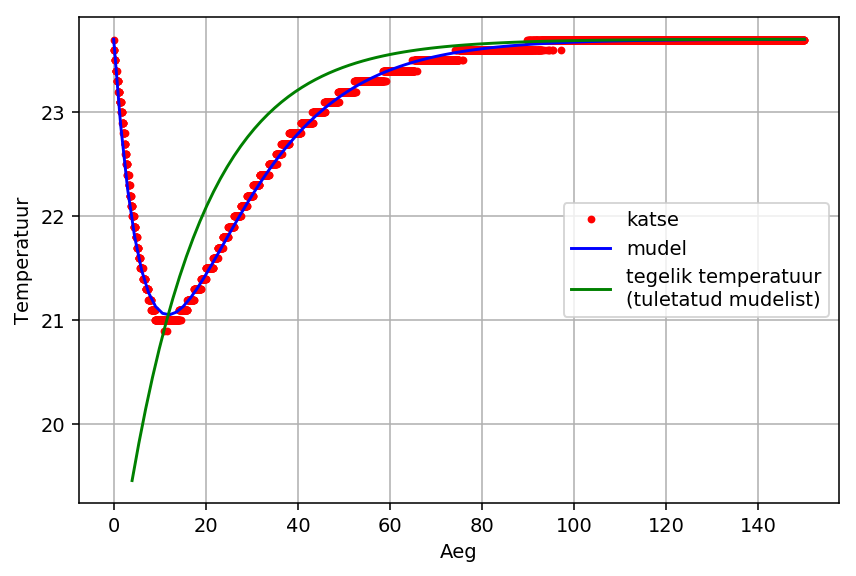
Oletagem, et andur reageerib viivitusega, mida iseloomustab kiiruskonstant $r$ (ühikutes 1/s), nii et järsu ja püsiva temperatuurimuutuse $\Delta T$ korral anduri signaal sõltuks ajast nii: $$T_\text{andur}(t)=T_0+\Delta T\left(1 - e^{-rt}\right),$$ kus $T_0$ on algtemperatuur. Eeldame, et keskkonna tegelik temperatuurikäik (aegadel $t>0$) on samuti sarnane eksponentfunktsiooniga ja seda iseloomustab kiiruskonstant $q$: $$T(t)=T_0 + A e^{-qt},$$ kus $A$ on algne temperatuurimuut (antud näite puhul negatiivne). Nende kahe protsessi sidumisel (soojusülekanne keskkonnast andurile) on võimalik leida anduri näit sõltuvana ajast: $$T(t)=T_0 + \frac{Ar}{r - q}\left(e^{-qt} - e^{-rt}\right).$$ Vastavat sobitust kujutab sinine kõver eelneval graafikul, ja vastavat keskkonna temperatuuri käiku ($T_0 + A e^{-qt}$) roheline kõver.

Toodud arvutuskäik eeldas, et protsess algab täpselt hetkel $t=0$ (vajadusel tuleb ajatelge vastavalt nihutada). Lisaks eeldame, et algsest andmemassiivist on mudelile vastav ajavahemik juba välja lõigatud (nagu graafikul). Seega algoritm on järgmine:

def sobita_koste(aeg, signaal, p = None):
    mudel = lambda t, b, A, r, q: b + A * r * (exp(-q * t) - exp(-r * t)) / (r - q)
    if p is None:
        p = signaal[0], 1.5 * (np.amax(signaal) - signaal[0]), 20 / aeg[-1], 3 / aeg[-1]
    (b, A, r, q), _ = curve_fit(mudel, aeg, signaal, p)
    f = lambda t: mudel(t, b, A, r, q)
    g = lambda t: b + A * exp(-q * t)
    return (b, A, r, q), f, g

Selle kasutamine:

(b, A, r, q), f, g = sobita_koste(aeg, signaal)
plot(aeg, signaal, 'r.', label='katse')
plot(aeg, f(aeg), 'b-', label='mudel')
plot(aeg, g(aeg), 'g-', label='tegelik')
legend()
show()

Seega algtemperatuuri annab b + A ehk g(0).

Sisukord