Üksliikmeid nimetatakse sarnasteks, kui nad üksteisest üldse ei erine või kui nad erinevad ainult kordaja poolest.

Näiteks: N5a²bc⁴ ja (−0,2)⁷a²bc⁴ ning xy ja xy, kuid sarnased ei ole 2xy² ja 2x²y.

Üksliikmete liitmisel ja lahutamisel saadud avaldist nimetatakse üksliikmete algebraliseks summaks ehk hulkliikmeks. Nii on avaldis 2x² + 4xy − 0,75xyz − 12 hulkliige.

Üksliikmete koondamiseks nimetatakse sarnaste liikmete algebralise summa asendamist sellise liidetavatega sarnase üksliikmega, mille kordaja on võrdne liidetavate üksliikmete kordajate summaga.

Näide: koondades sarnased üksliikmed summas
2xy − 5xy + 6xy tuleb asendada see üksliikmega (2 − 5 + 6)xy = 3xy.

Hulkliikme koondamine tähendab antud hulkliikme esitamist kujul, milles kõik sarnased üksliikmed on koondatud.

Näide:

4x² − 3x + 7 − 8x² + x − 2 = −4x² − 2x + 5

3xy² + 5x − 6xy² − 2xy + 2xy² − 5xy − z = −xy² − 7xy + 5x − z.

Et teha tehteid üks- ja hulkliikmetega, on vaja meelde tuletada tehted astmetega:

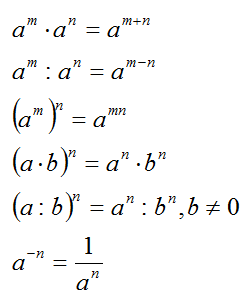
Kontrollige alljärgnevaid teste lahendades, kas oskate neid reegleid kasutada.

I test:

II test: