


Kombinatoorika on matemaatika haru, mis uurib etteantud hulga elementide kombineerimise võimalusi. Kuna selliste võimaluste arv on sageli väga suur, tuleb kõigi variantide töötlemist nõudvad ülesanded arvutile usaldada. Käesolevas peatükis vaatlemegi põhilisi kombinatoorseid objekte ja nendega seotud algoritme.
6.1 Kombinatoorika põhimõisted
Kombinatoorseid algoritme võib liigitada mitme tunnuse alusel. Kaks loomulikumat liigitust on töödeldavate objektide liikide ja nende objektidega sooritatavate tegevuste alusel.
6.1.1 Kombinatoorsed objektid
Kombineeritavate elementide hulka nimetatakse põhihulgaks (ingl base set). Üldiselt võivad selle elementideks olla mistahes objektid, aga arvutis on muidugi kõige mugavam kasutada arve ja seepärast eeldame edaspidi, et m-elemendiline põhihulk on alati M = {1, ..., m}. See pole kuigi oluline kitsendus, sest kui mõnes praktilises ülesandes on vaja kombineerida muid objekte, võime tegelikke objekte hoida eraldi massiivis ja kasutada hulga M elemente indeksitena objektide sellest massiivist leidmisel.
Lihtsaim kombinatoorne objekt on järjend ehk ennik (ingl tuple), mis koosneb fikseeritud arvust põhihulga elemendidest. Kaht järjendit loetakse võrdseks, kui nende pikkused ja vastavatel positsioonidel olevad elemendid on samad.
Näiteks põhihulga M = {1,2,3} korral saame moodustada 9 erinevat 2-elemendilist järjendit (ehk lühemalt 2-järjendit): (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2) ja (3,3).
Permutatsiooni (ingl permutation) ehk ümberjärjestuse puhul nõutakse lisaks, et põhihulga iga element võib permutatsioonis esineda maksimaalselt ühe korra.
Eelmise näite põhihulga korral on erinevaid 2-elemendilisi permutatsioone (ehk 2-permutatsioone) kokku 6: (1,2), (1,3), (2,1), (2,3), (3,1) ja (3,2).1
Ka kombinatsioon (ingl combination) võib, sarnaselt permutatsiooniga, sisaldada põhihulga iga elementi maksimaalselt ühes eksemplaris. Erinevus on selles, et kaks kombinatsiooni loetakse erinevateks ainult juhul, kui nende elementide hulgad (järjestusest hoolimata) on erinevad.
Kahes eelmises näites vaadeldud põhihulga korral on erinevaid 2-kombinatsioone vaid 3: {1,2}, {1,3} ja {2,3}.2
Hulga tükelduseks (ingl partition) nimetatakse selle jagamist mittetühjadeks alamhulkadeks nii, et põhihulga iga element kuulub täpselt ühte alamhulka. Kaht tükeldust loetakse erinevateks, kui leiduvad kaks elementi, mis ühes tükelduses on samas alamhulgas, aga teises erinevates.
Näiteks 3-elemendilisel põhihulgal on 5 erinevat tükeldust: {{1,2,3}} (``tükeldus'' koosneb ühest tükist); {{1,2},{3}}, {{1,3},{2}}, {{2,3},{1}} (tükeldused kaheks tükiks) ja {{1},{2},{3}} (tükeldus kolmeks tükiks).
Kuigi sellega pole kombinatoorsete objektide liigid kaugeltki ammendatud, on meil nüüdseks juba piisavalt näiteid, et vaadelda lähemalt, millised on põhilised kombinatoorikaülesanded.
6.1.2 Kombinatoorsed ülesanded
Üks ilmsemaid kombinatoorikaülesandeid on kõigi vastavat liiki objektide genereerimine (ingl generation) ehk loetlemine (ingl enumeration)3, see tähendab kõigi objektide nimekirja koostamine.
Vahel pole meil aga vaja mitte objekte endid, vaid ainult nende arvu. Muidugi võib loendamise (ingl counting) ülesande (vähemalt teoreetiliselt) alati taandada genereerimisele --- kui meil on olemas meid huvitavate objektide nimekiri, võime nende arvu teadasaamiseks nad vahetult üle lugeda. Aga sageli on objektide arvu võimalik leida ka oluliselt efektiivsemalt.
Kombinatoorse otsimise (ingl searching) ülesandes nõutakse kõigi objektide hulgast ainult teatud tingimusele vastava(te) objekti(de) leidmist. Kui tingimuseks on mingi hinnangufunktsiooni minimeerimine või maksimeerimine, nimetatakse seda ülesannet ka kombinatoorse optimeerimise (ingl optimization) ülesandeks.
6.2 Loendamine
Ajalooliselt olid loendamisülesanded kombinatoorika üks esimesi praktilise väärtusega rakendusi --- loendamisel põhineb tõenäosustooria, ja sellel omakorda põhinevad hasartmängud.
Lihtsamate ja korrapärasemate objektide korral on loendamisülesanded sageli lahendatavad ka arvuti abita. Arvutusvahendist sõltumata on loendamisel väga kasulikud kaks põhireeglit: korrutamisreegel ja liitmisreegel.
6.2.1 Korrutamisreegel
Korrutamisreegel ütleb, et kui meil on vaja teha järjest kaks valikut ning esimese valiku tegemiseks on v1 võimalust ja iga esimese valiku järel on teise valiku tegemiseks v2 võimalust, siis nende kahe valiku tegemiseks on kokku v1 · v2 võimalust.
Selle reegli põhjal on lihtne leida m-elemendilise põhihulga n-järjendite arv: järjendi iga elemendi valimiseks on meil täpselt m võimalust, seega on kõigi n elemendi valimiseks kokku
T(m, n) = m · m · ... · mn = mn
võimalust.
Ka permutatsioonide arv on leitav korrutamisreegli abil: permutatsiooni esimese elemendi valimiseks on meil kogu põhihulk, seega m võimalust; teiseks elemendiks ei tohi me valida juba valitud elementi, seega jääb m - 1 võimalust; kolmandaks ei tohi me valida kumbagi juba valitud elementi, seega jääb m - 2 võimalust. Samal moel jätkates saame, et m-elemendilise põhihulga n-permutatsioonide arv on
|
P(m, n) = m · (m - 1) · ... · (m - (n - 1)) = |
|
,
(6.1) |
P(
m) =
P(
m,
m) =
m!.
(6.2)
Korrutamisreeglit võib kasutada ka tagurpidi, jagamisreeglina: kui on teada, et kahe järjestikuse valiku tegemise võimaluste koguarv on v ja et mistahes esimese valiku järel on teist valikut võimalik teha v2 erineval viisil, saame sellest avaldada esimese valiku tegemise võimaluste arvu v1 = v / v2.
Näiteks kombinatsioonide arvu leidmine on jagamisreegli abil tunduvalt mugavam kui korrutamisreegli abil. Korrutamisreegli kasutamist raskendab asjaolu, et sama kombinatsiooni korduva loendamise vältimiseks tuleks elemente kombinatsiooni lisada mingis kindlas järjekorras (näiteks kasvavas). Siis aga sõltub teise elemendi valimise võimaluste arv sellest, millise elemendi me esimeseks valisime ja korrutamisreeglit ei saa enam rakendada.
Hoopis lihtsam on lähtuda tähelepanekust, et igast n-kombinatsioonist (mis on lihtsalt põhihulga n-elemendiline alamhulk) saab valemi 6.2 kohaselt moodustada P(n) = n! erinevat n-permutatsiooni. Pole raske veenduda, et nii saame koostada kõik võimalikud n-permutatsioonid, ja seejuures igaühe täpselt ühe korra. Valemi 6.1 ja jagamisreegli põhjal saame seega n-kombinatsioonide arvuks
6.2.2 Liitmisreegel
Liitmisreegel ütleb, et kui meil on vaja teha üks kahest valikust ning esimese valiku tegemiseks on v1 võimalust ja teise tegemiseks v2 võimalust, siis neist kahest valikust ühe tegemiseks on kokku v1 + v2 võimalust. Seejuures on oluline, et nende kahe valiku võimaluste hulgad peavad olema ühisosata.
Selle reegli abil on lihtne leida rekurrentne valem m-elemendilise põhihulga n-kombinatsioonide arvu loendamiseks: kõik n-kombinatsioonid võime jagada kaheks selle põhjal, kas nad sisaldavad või ei sisalda elementi m.
Igast elementi m sisaldavast n-kombinatsioonist saame selle eemaldamisega (m - 1)-elemendilise põhihulga (n - 1)-kombinatsiooni. Iga elementi m mittesisaldav n-kombinatsioon on automaatselt ka (m - 1)-elemendilise põhihulga n-kombinatsioon.
Kuna need variandid on teineteist välistavad (ei ole võimalik, et mingi kombinatsioon kuulub mõlemasse alamhulka) ja katavad kõik võimalused (ei ole võimalik, et mingi kombinatsioon ei kuulu kumbagi alamhulka), siis saamegi liitmisreegli põhjal, et C(m, n) = C(m - 1, n - 1) + C(m - 1, n).
Lisades sellele valemile veel ääretingimused C(m, 0) = 1 (ainus 0-kombinatsioon on tühi hulk) ja C(m, m) = 1 (ainus m-kombinatsioon on põhihulk ise), ongi käes rekursiivse programmi koostamiseks piisav tulemus
|
C(m, n) = |
ì
í
î |
|
1, |
kui n = 0, |
| 1, |
kui n = m, |
| C(m - 1, n - 1) + C(m - 1, n), |
kui 0 < n < m. |
|
(6.4) |
Kuna valemid 6.3 ja 6.4 loendavad samasid objekte, siis on igati ootuspärane, et nende alusel kirjutatud programmid annavad ka ühesuguseid tulemusi.
Hulga tükelduste loendamine on eelmistest veidi tülikam ülesanne. Selle lahendamiseks tuleb liitmisreeglit rakendada kaks korda.
Esmalt paneme tähele, et m-elemendilise hulga kõigi tükelduste arvud B(m) (ehk Belli arvud) avalduvad n tükiks tükelduste arvude S(m, n) (ehk Stirlingi teist liiki arvude) kaudu:
Liitmisreegli veelkordse kasutamisega saame rekurrentse võrrandi Stirlingi arvude avaldamiseks, arvestades, et m-hulga tükeldused on saadavad (m - 1)-hulga tükeldustest järgmiselt: igast (m - 1)-hulga (n - 1)-tükeldusest saame m-hulga n-tükelduse, kui lisame sellele eraldi tükina elemendi m; igast (m - 1)-hulga n-tükeldusest saame n erinevat m-hulga n-tükeldust, kui lisame elemendi m kordamööda igaühele olemasolevast n tükist. Pole raske veenduda, et saadud variandid on kõik erinevad ja katavad ühtlasi ka kõik võimalikud m-hulga n-tükeldused. Seega saame nende koguarvuks S(m, n) = n · S(m - 1, n) + S(m - 1, n - 1).
Lisades sellele valemile ääretingimused S(m, 1) = 1 (ainus 1-elemendiline tükeldus on põhihulk ise) ja S(m, m) = 1 (ainus m-tükeldus on selline, kus iga element on omaette alamhulk), ongi käes programmeerimiseks kõlblik
| S(m, n) = |
ì
í
î |
|
1, |
kui n = 1, |
| 1, |
kui n = m, |
| n · S(m - 1, n) + S(m - 1, n - 1), |
kui 1 < n < m. |
|
Ka liitmisreeglit on võimalik pöörata lahutamisreegliks.
Näiteks selleks, et leida 1 ja 100 vahele jäävate kolmega mittejaguvate täisarvude arv, on lihtsam leida kõigepealt kolmega jaguvate täisarvude arv (mis on loomulikult 33) ja siis järeldada, et kõik ülejäänud 100 - 33 = 67 arvu peavad olema kolmega mittejaguvad.
6.2.3 Elimineerimismeetod
Elimineerimismeetod (ingl inclusion-exclusion principle) aitab leevendada liitmisreegli (praktikas üsnagi ahistavat) nõuet, et valikuvariantide hulgad peavad olema ühisosata.
Näiteks 1 ja 100 vahele jäävate kolme või viiega jaguvate arvude loendamiseks liitmisreeglit kasutada ei saa, sest need variandid pole teineteist välistavad --- leidub ka arve, mis jaguvad nii kolme kui viiega.
Alamhulkade lõikumatuse nõude ignoreerimisel saame tõesti vale vastuse: 1 ja 100 vahel on kolmega jaguvaid arve 33 ja viiega jaguvaid 20, kuid kolme või viiega jaguvaid 47, mitte 33 + 20 = 53.
Vea põhjuseks on muidugi asjaolu, et arve, mis jaguvad nii kolme kui viiega, loeme topelt --- ühe korra kui kolmega, teise korra kui viiega jaguvaid. Topelt loeme seega kõiki 15-ga jaguvaid arve, mida uuritaval lõigul on 6. Õige vastuse saamiseks tuleb topelt loetud variantide arv lõppsummast maha lahutada: 33 + 20 - 6 = 47.
Sama kehtib mistahes kahe tunnusega objektide loendamisel (joonisel 6.1 vasakul): kui n1 objektil on esimene tunnus (ja võib-olla samaaegselt ka teine) ja n2 objektil on teine tunnus (ja võib-olla samaaegselt ka esimene) ning n12 objektil on mõlemad tunnused, siis vähemalt üks neist kahest tunnusest on kokku n = n1 + n2 - n12 objektil.
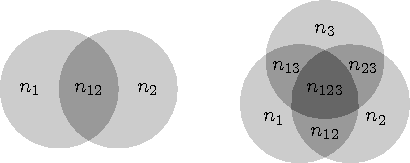
Joonis 6.1: Elimineerimismeetod
Kolme erineva tunnuse korral (joonisel 6.1 paremal) oleme ühe tunnusega objektide arvude liitmisel ja kahe tunnusega objektide arvude lahutamisel kõigi kolme tunnusega objektide arvu lisanud summasse kolm korda (n1, n2 ja n3 hulgas) ja ka lahutanud kolm korda (n12, n13 ja n23 hulgas), seega on need objektid sisuliselt loendamata ja õige tulemuse saamiseks tuleb neid eraldi arvestada (n123).
Näiteks 1 ja 100 vahele jäävate kahe, kolme või viiega jaguvate arvude loendamiseks peame arvestama, et: kahega jaguvaid arve on 50, kolmega jaguvaid 33, viiega jaguvaid 20; kahe ja kolmega jaguvaid 16, kahe ja viiega jaguvaid 10, kolme ja viiega jaguvaid 6; kõigi kolmega jaguvaid 3. Seega on kahe, kolme või viiega jaguvaid arve kokku 50 + 33 + 20 - 16 - 10 - 6 + 3 = 74.
Üldiselt, t erineva tunnuse korral on vähemalt ühe tunnusega objektide koguarv
kus Ni tähistab vähemalt i tunnusega objektide arvude summat, kusjuures iga i korral tuleb vaadelda kõiki võimalikke i erineva tunnuse kombinatsioone.
6.3 Genereerimine
Genereerimisel, erinevalt loendamisest, peame mõtlema ka sellele, millises järjekorras me tulemust saada tahame.
Elementide loeteluna esitatavate kombinatoorsete objektide (järjendid, permutatsioonid, kombinatsioonid) puhul peetakse üldiselt standardseimaks leksikograafilist (ingl lexicographical) järjestust --- kahe objekti võrdlemisel jäetakse vahele need elemendid kummagi objekti algusest, mis on omavahel võrdsed ja otsus langetatakse esimese erineva elemendi põhjal.
Mõnikord on kasulikum objekte genereerida minimaalse muutuse (ingl minimal change) järjestuses --- tulemuste hulgas järjest olevate objektide erinevus peab olemas minimaalne. Minimaalsuse definitsioon sõltub muidugi konkreetsest objektist ja vahel ka sellest, milleks neid objekte kasutatakse.
Näiteks permutatsioone on võimalik järjestada nii, et iga järgmine on saadav eelmisest kahe kõrvutioleva elemendi vahetamise teel, järjendeid aga nii, et iga järgmine erineb eelmisest ainult ühes positsioonis ühe võrra.
| Leksikograafiline |
Minimaalse muutuse |
| (1,2,3) |
(1,2,3) |
| (1,3,2) |
(1,3,2) |
| (2,1,3) |
(3,1,2) |
| (2,3,1) |
(3,2,1) |
| (3,1,2) |
(2,3,1) |
| (3,2,1) |
(2,1,3) |
Table 6.1: Hulga {1,2,3} permutatsioonide järjestusi
| Leksikograafiline |
Minimaalse muutuse |
| (1,1,1) |
(1,1,1) |
| (1,1,2) |
(1,1,2) |
| (1,2,1) |
(1,2,2) |
| (1,2,2) |
(1,2,1) |
| (2,1,1) |
(2,2,1) |
| (2,1,2) |
(2,2,2) |
| (2,2,1) |
(2,1,2) |
| (2,2,2) |
(2,1,1) |
Table 6.2: Hulga {1,2} 3-järjendite järjestusi
Edasi tegeleme objektide genereerimisega leksikograafilises järjekorras.
6.3.1 Tagurdusmeetod
Väga üldine meetod igasugusteks variantide genereerimiseks on tagurdusmeetod (ingl backtracking). Selle põhiideed illustreerib näide 1: tegemist on rekursiivse algoritmiga, mis saab osaliselt valmis genereeritud variandi (parameeter v), leiab kõik võimalikud sammud selle täiendamiseks (loetelu w1 kuni wn) ja proovib jätkata genereerimist iga võimaliku täiendatud variandiga (abimuutuja v'). Kui mõni täiendatud variantidest osutub täielikuks (tingimus real 1), kasutame selle ära (näiteks väljastame) ja jätkame uute variantide genereerimist.
Tagurdusmeetodi kasutamiseks tuleb selle esimesel väljakutsel (kas põhiprogrammist või mõnest teisest alamprogrammist) anda kaasa seeme (ingl seed) --- lähtepunkt, millest kõigi teiste konstrueerimist alustada. Tavaliselt on seemneks mingis mõttes tühi variant.
Algoritm 1
GenRek: Variantide genereerimine rekursiivselt
Sisend: v --- osaline variant
Väljund: leiab kõik võimalused v täiendamiseks
-
kui v on täielik variant
-
--- kasutame v
-
muidu
-
--- vatleme kõiki v täiendamise võimalusi
-
korda w Î w1 ... n
-
v'¬v + w
-
--- invariant: v' on suurem osaline variant
-
GenRek(v')
-
--- tagurdus: proovime v järgmist täiendusvõimalust
-
lõppkorda
-
lõppkui
Väga lihtne on tagurdusmeetodil genereerida näiteks järjendeid (algoritm 2): n-järjendi genereerimisesl on osaliseks variandiks mingi k-järjend (kus k £ n) ja täiendamise üks samm on elemendi ak+1 lisamine antud k-järjendi lõppu.
Nagu järjendite loendamisel juba mainitud, on selle sammu tegemiseks m võimalust --- uueks elemendiks võime ilma piiranguteta valida ükskõik millise põhihulga elemendi.
Seemneks on tühi (0-elemendiline) järjend.
Algoritm 2
JarjRek: Järjendite genereerimine rekursiivselt
Sisend: a1 ... k on k-järjend
-
kui k = n
-
--- a1 ... n on leitud n-järjend
-
muidu
-
korda ak+1¬1 ... m
-
--- invariant: a1 ... k+1 on (k+1)-järjend
-
JarjRek(a1 ... k+1)
-
lõppkorda
-
lõppkui
Permutatsioonide genereerimine (algoritm 3) erineb järjendite genereerimisest ainult permutatsiooni definitsioonist lähtuva kitsenduse võrra: etteantud k-permutatsiooni lõppu lisatava elemendi valimisel peame kontrollima, et see element permutatsioonis eespool juba kasutusel ei ole.
Selle kontrolli tõhusaks realiseerimiseks kasutatakse tavaliselt globaalset massiivi v1 ... m, mille element vi näitab, kas põhihulga element i on veel vaba. Siis taandub real 5 oleva tingimuse kontrollimine selle massiivi ühe elemendi väärtuse uurimisele, kuid selle eest peame enne rekursiivset väljakutset real 7 elemendi ak+1 jooksva väärtuse kasutatuks märkima ja pärast rekursioonist naasmist selle elemendi jälle vabastama.
Algoritm 3
PermRek: Permutatsioonide genereerimine rekursiivselt
Sisend: a1 ... k on k-permutatsioon
-
kui k = n
-
--- a1 ... n on leitud n-permutatsioon
-
muidu
-
korda ak+1¬1 ... m
-
kui ak+1 Ïa1 ... k
-
--- invariant: a1 ... k+1 on (k+1)-permutatsioon
-
PermRek(a1 ... k+1)
-
lõppkui
-
lõppkorda
-
lõppkui
Kombinatsioonide genereerimisel (algoritm 4) on kasulik uusi elemente kombinatsiooni lisada kasvavas järjekorras --- nii on lihtne hoiduda sama elemendi korduvast lisamisest ja on välistatud ka samade elementide ümberjärjestuste eksikombel erinevateks kombinatsioonideks lugemine.
Algoritm 4
KombRek: Kombinatsioonide genereerimine rekursiivselt
Sisend: a1 ... k on k-kombinatsioon
Abimuutujad: x --- vähim vaba element
-
kui k = n
-
--- a1 ... n on leitud n-kombinatsioon
-
muidu
-
kui k = 0
-
x¬1
-
muidu
-
x¬ak + 1
-
lõppkui
-
korda ak+1¬x ... m
-
--- invariant: a1 ... k+1 on (k+1)-kombinatsioon
-
KombRek(a1 ... k+1)
-
lõppkorda
-
lõppkui
6.3.2 Iteratsioonimeetod
Teine üldisem võimalus on genereerida objekte iterativselt.
Iteratiivse generaatori struktuur on toodud näites 5: kõigepealt luuakse esimene otsitav objekt vahetult ja edasi leitakse igal sammul jooksva objekti põhjal järgmine.
Algoritm 5
GenIte: Variantide genereerimine iteratiivselt
Abimuutujad: v --- jooksev variant
-
v¬EsimeneVariant
-
senikui v ¹ Ø
-
--- kasutame v
-
v¬JargmineVariant(v)
-
lõppsenikui
Nagu üldiselt iteratiivsete generaatorite puhul, nii on ka järjendite genereerimisel põhiline jooksva järjendi põhjal uue leidmine (algoritm 6): suurendada tuleb kõige parempoolsemat positsiooni, mille suurendamine on võimalik; kõik sellest positsioonist paremal pool olevad peavad olema maksimaalse võimaliku väärtusega (muidu oleks ju võimalik suurendada mõnda neist) ja järgmises järjendis peavad nende väärtused jälle vähimast alustama.
(Sisuliselt on tegemist ühe liitmisega n-kohalisele m-süsteemi arvule. Tõenäoliselt oleks seda kergem märgata, kui põhihulk oleks {1 ... m} asemel {0 ... m-1}.)
Algoritm 6
JrgmJarj
Sisend: a1 ... n on n-järjend
Väljund: leksikograafiliselt järgmine n-järjend
Abimuutujad: u Î {0,1} --- jooksev ülekanne
-
u¬1
-
korda i¬n ... 1
-
ai¬ai + u
-
kui ai > m
-
ai¬1
-
muidu
-
u¬0
-
lõppkui
-
lõppkorda
-
kui u = 0
-
tagasta v
-
muidu
-
tagasta Ø
-
lõppkui
6.4 Otsimine
Üldiselt on otsimis- ja optimeerimisülesanded kombinatoorikas kõige loomingulisemad. Põhiline lahendusmeetod on variantide genereerimine rekursiivselt, kusjuures algoritmi töö kiirendamiseks püütakse võimalikult vara aru saada, kui parasjagu käsilolevat osalist varianti ei ole võimalik kõiki ülesande tingimusi rahuldavaks täielikuks variandiks välja arendada.
Otsimisülesande näitena vaatleme ülesannet paigutada N lippu N × N malelauale nii, et mitte ükski neist poleks ühegi teise tule all.
Esiteks paneme kohe tähele, et iga lipp peab laual olema eraldi real --- samal real olevad lipud tulistaks üksteist kindlasti. See aga tähendab, et me võime kõik potentsiaalsed lahendused märkida üles kujul a1 ... N, kus ak näitab k. real oleva lipu veerunumbrit.
Edasi võime hakata lippude paigutuse variante järjest läbi proovima. Seda on kasulik teha tagurdusmeetodil, sest nii saame k. lipu paigutamisel kohe kontrollida, et see ei jää juba varem laual olevate lippude (1 ... k-1) tule alla ja mitte kulutada aega ülejäänud lippude (k+1 ... N) paigutamisele, kuna seisu muudab kõlbmatuks ka üksainus tule alla jäänud lipp. Lahenduse töökiiruse seisukohalt on oluline, kuidas me hoiame infot tule all olevate väljade kohta.
Üks võimalus on seda infot eraldi üldse mitte hoida ja võrrelda iga uue lipu paigutamisel selle asukohta laual kõigi varem paigutatud lippude omadega --- iga lipu korral tuleb kontrollida, kas uus on temaga samas veerus või samal diagonaalil, seega kulutame k. lipu iga positsiooni kontrollimiseks O(k) operatsiooni.
Teine võimalus on iga lipu lauale paigutamisel märkida ära kõik väljad, mida see lipp tule all hoiab. Siis on küll võimalik uuele lipule koha valimisel selle koha kõlblikkuse või kõlbmatuse üle väga kiiresti otsustada, aga lipu lauale paigutamine ja selle sealt eemaldamine muutuvad ebaefektiivseks --- N × N laual võib lipp tulistada maksimaalselt 4 · N - 3 välja.
Kõige parema lahenduse saame, pannes tähele, et laual võib olla ülimalt üks lipp igas veerus ning igal tõusval ja igal langeval diagonaalil. Jääb veel leida efektiivne viis neid kolme liiki objekte hõivatuks ja vabastatuks märkida (nagu põhihulga elementide haldamisel permutatsioonide genereerimisel).
Veergude haldamine on muidugi lihtne --- selleks võime kasutada massiivi v1 ... N. Aga osutub, et ka diagonaalidega pole palju rohkem muret. Nimelt on igal tõusval diagonaalil rea- ja veerunumbri vahe ühe diagonaali piires sama ja erinevatel diagonaalidel erinev --- seega võib nende olekute hoidmiseks kasutada massiivi td1-N ... N-1. Langeva diagonaali identifitseerimiseks sobib rea- ja veerunumbri summa --- seega võib nende olekute hoidmiseks kasutada massiivi ld2 ... 2 · N.
Algoritm 7
Lipud: Lippude paigutamine malelauale
Sisend: r --- rida, millele lippu paigutame
-
kui r > n
-
--- on leitud n lipu paigutus
-
muidu
-
korda x¬1 ... N
-
kui vx = vaba Ù tdr-x = vaba Ù tlr+x = vaba
-
--- invariant: positsioon (r,x) on vaba
-
vx¬kinni; tdr-x¬kinni; tdr+x¬kinni
-
Lipud(r+1)
-
vx¬vaba; tdr-x¬vaba; tdr+x¬vaba
-
lõppkui
-
lõppkorda
-
lõppkui
Optimeerimisülesannete puhul on sageli kasulik hoida eraldi infot parima seni leitud lahenduse kohta ja hinnata iga variandi töötlemisel, kas on üldse võimalik, et selle edasiarendamisel võiks saada parema lahenduse. Kui see pole võimalik, pole ka mõtet seda varianti edasi töödelda.
Ülesanded
Ülesanne 1
Kui palju on standardses 52-kaardilises pakis (kaks punast ja kaks musta masti, igas mastis 9 numbri- ja 4 pildilehte) kaarte, mis on:
| (a) punased? |
| (b) numbrid? |
| (c) punased ja numbrid? |
| (d) punased ja mitte numbrid? |
| (e) punased või numbrid? |
| (f) punased või numbrid, kuid mitte mõlemat korraga? |
Vastata ilma kaarte vahetult loendamata. Põhjendada kõiki oma vastuseid.
Ülesanne 2
Tavalist 6-tahulist täringut visatakse viis korda. Mitmel erineval viisil on võimalik saada viie viske summas paarisarv silmi? Põhjendada oma vastust.
Ülesanne 3
Kirjutada iteratiivne programm m-hulga m-permutatsioonide genereerimiseks leksikograafilises järjekorras.
Ülesanne 4
Kirjutada iteratiivne programm m-hulga n-kombinatsioonide genereerimiseks leksikograafilises järjekorras.
Ülesanne 5
Põhihulga M = {1, ..., m} korratuseks (ingl derangement) nimetatakse m-permutatsiooni P = (p1, p2, ..., pm), milles ükski element ei asu ``oma õigel kohal'', s.t. " i Î M : pi ¹ i. Tõestada korratuste arvude D(m) võrrand D(m) = (m - 1) · (D(m - 1) + D(m - 2)). Määrata vajalikud ääretingimused ja kirjutada programm korratuste loendamiseks.
Ülesanne 6
Kirjutada rekursiivne programm korratuste genereerimiseks leksikograafilises järjekorras.
Ülesanne 7
Kirjutada iteratiivne programm korratuste genereerimiseks leksikograafilises järjekorras.
Ülesanne 8
Kirjutada programm, mis paigutab N × N lauale maksimaalse hulga maleratsusid nii, et mitte ükski neist poleks ühegi teise tule all.
Kirjandus
- Reimo Palm. Diskreetse matemaatika elemendid. Tartu Ülikool, 2003.
- Sissejuhatus diskreetsesse matemaatikasse, sealhulgas ka kombinatoorika alustesse. Matemaatilisema kallakuga. 160 lk.
- Donald L. Kreher, Douglas R. Stinson. Combinatorial Algorithms: Generation, Enumeration, and Search. CRC Press, 1999.
- Kombinatoorika algoritmide õpik. 330 lk.
Aadressil http://www.math.mtu.edu/~kreher/cages.html on muu hulgas ka algoritmide realisatsioonid C's, kuid ilma raamatu endata on neid väga raske kasutada.
- Витольд Липский. Комбинаторика для программистов. Мир, 1988.
- Eelmisest vanem ja veidi õhem, põhimõtteliselt üsna sarnane. 213 lk.
- Ülo Kaasik, Uno Kaljulaid. Kombinatoorika analüütilisi ja algebralisi meetodeid. Tartu Ülikool, 1993.
- Kombinatoorika loengukonspekt. Üsna tõsine matemaatika. 159 lk.
- Dany Breslauer, Devdatt P. Dubhasi. Combinatorics for Computer Scientists. University of Aarhus, 1995.
- Kombinatoorika loengukonspekt. Tõsine matemaatika. 330 lk.
http://www.brics.dk/BRICS/LS/95/4/BRICS-LS-95-4.ps.gz
- 1
- Mõnedes vanemates raamatutes nimetatakse m-elemendilise põhihulga korral permutatsioonideks ainult m-permutatsioone ja k < m korral räägitakse k-variatsioonidest.
- 2
- Kuna kombinatsioonid on põhihulga alamhulgad, märgitaksegi neid tavaliselt hulkadena, andes elementide loetelu ümarsulgude asemel looksulgudes.
- 3
- NB! Inglise keeles kasutatakse sõna `enumerate' nii `loetlema' kui ka `loendama' tähenduses.









