Katses on mõõdetud anduri signaal sõltuvana ajast, ja hiljem on tarvis sellest välja lugeda vastava füüsikalise suuruse väärtus teatud ajahetkel. Juhul kui andur on parajalt suure lahutusvõimega ja signaal on ilma märgatava mürata, võib kasutada interpoleerimist. Vastasel korral võiks toorest signaali mingil määral keskmistada (eriti kui andmepunkte on palju).

Kui signaal on eeldatavasti konstantne (nt stabiliseerunud temperatuur), piisab keskväärtuse arvutamisest üle teatud hulga naaberpunktide:

def leia_näit(aeg, signaal, hetk, delta):
    valitud = (aeg >= hetk - delta) & (aeg <= hetk + delta)
    return signaal[valitud].mean()


hetk = 50
delta = 5
näit = leia_näit(aeg, signaal, hetk, delta)

plot(aeg, signaal, 'b.')
plot(hetk, näit, 'ro')
axvspan(hetk - delta, hetk + delta, color='r', alpha=0.2)
xlabel('Aeg')
grid()
tight_layout()
show()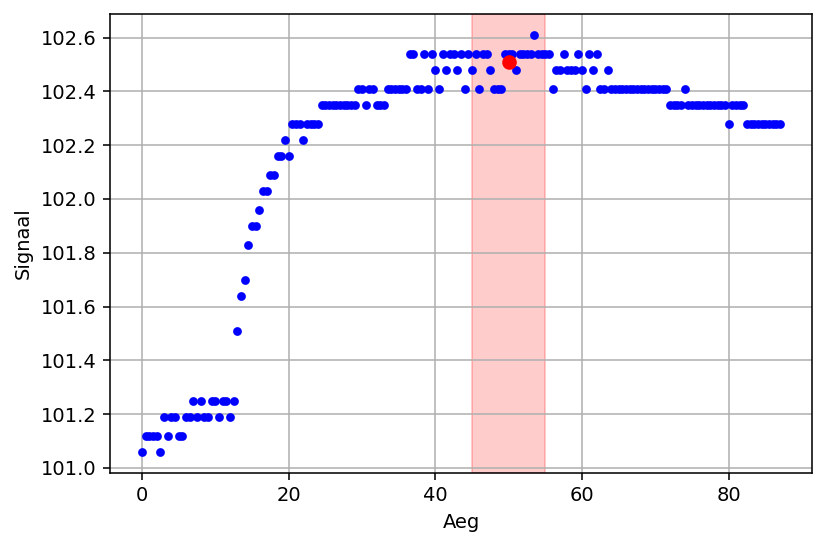

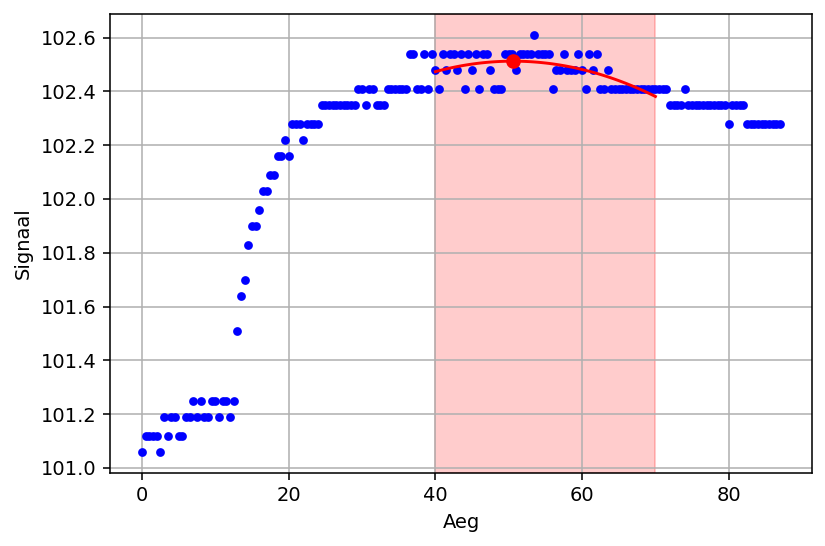
Signaali miinimumi või maksimumi leidmisel (nagu antud näites) tuleks pigemini sobitada parabool. Viimase abiga on võimalik see miinimum või maksimum ka automaatselt lokaliseerida, nii et seda ei pea enam silma järgi tegema:

def leia_näit(aeg, signaal, algus, lõpp, punkte=100):
    valitud = (aeg >= algus) & (aeg <= lõpp)
    a, b, c = np.polyfit(aeg[valitud], signaal[valitud], 2)
    
    # igaks juhuks arvutame leitud parabooli, et saaks selle kuvada graafikul
    x = np.linspace(algus, lõpp, punkte)  
    y = np.polyval((a, b, c), x)
    
    return -b / (2 * a), c - b**2 / (4 * a), (x, y)


algus, lõpp = 40, 70
hetk, näit, parabool = leia_näit(aeg, signaal, algus, lõpp)

plot(aeg, signaal, 'b.')
plot(*parabool, 'r-')
plot(hetk, näit, 'ro')
axvspan(algus, lõpp, color='r', alpha=0.2)
xlabel('Aeg')
ylabel('Signaal')
grid()
tight_layout()
show()

Sisukord