Within the framework of this course of lectures, we study curves and surfaces using the methods of differential and integral calculus. We consider curves both in a plane and in 3-dimensional space, and surfaces in 3-dimensional space. Both a plane and 3-dimensional space are Euclidean.
An important part of the entire course of lectures are differential forms. In this course we consider the theory of differential forms in 3-dimensional Euclidean space. Another important concept studied in this course is the concept of connection. Using differential forms, we derive Cartan's structure equations for a connection 1-form and, as an example, calculate a connection form in curvilinear coordinates.
The main points in the theory of curves are the following
- Arc-length parametrization of a curve
- Curvature and torsion of a space curve
- Frenet-Serret (Bartels) equations
The main points in the theory of surfaces are the following
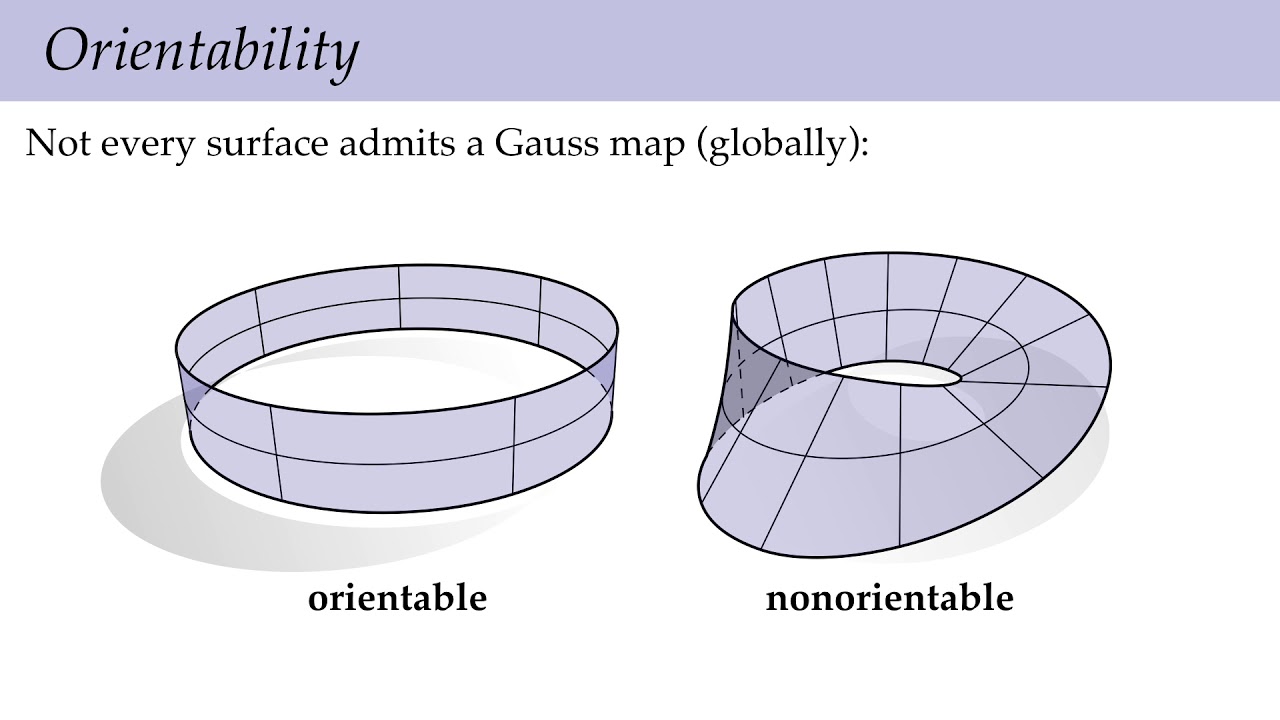
- Normal curvature, principal curvatures, Gauss curvature, mean curvature
- Fundamental Equations of a surface
- Isothermal parametrization, minimal surfaces
- Notion of a Riemann surface
- Gauss-Bonnet theorem