- Eessõna
- 1 Sissejuhatus
- 2 Tõenäosus
- 3 Diagnostilised testid
- 4 Kirjeldav statistika
- 5 Statistilised hinnangud
- 6 Statistiline hüpoteeside testimine
- 6.1 Ühe valimi z-testi ja t-testi eeldused
- 6.2 z-test protsendi võrdlemiseks konstandiga
- 6.3 I ja II liiki viga
- 6.4 Mõned lihtsamad statistilised testid
- 6.4.1 Ühe valimi z-test (1 keskväärtus või 1 protsent)
- 6.4.2 Ühe valimi t-test (1 keskväärtus)
- 6.4.3 Märgitest (1 protsent)
- 6.4.4 Kahe sõltumatu valimi z-test (2 keskväärtust või 2 protsenti)
- 6.4.5 Kahe sõltumatu valmi t-test (2 keskväärtust)
- 6.4.6 Wilcoxoni astaksumma test (2 mediaani*)
- 6.4.7 Paarisvaatluste t-test (keskväärtus enne ja pärast)
- 6.4.8 Wilcoxoni astakmärgitest (mediaan enne ja pärast*)
- 6.4.9 hii-ruut test (mitu protsenti)
- 6.4.10 Fisheri täpne test (mitu protsenti*)
- 6.4.11 Bartletti test (mitu protsenti*)
- 6.4.12 McNemari test (protsent* enne ja pärast)
- 6.4.13 F-test ja ANOVA
- 6.4.14 Kruskal-Wallise astaksumma test (mitu mediaani*)
- 6.4.15 Shapiro-Wilki test (normaaljaotuse kontrollimine)
- 6.4.16 Permutatsioonitest (universaalne*)
- 6.5 Mitmene võrdlemine
- 6.6 Ühepoolsed testid
- 7 Korrelatsioon
- 8 Regressioonanalüüs
- 9 Elukestusanalüüs
- 10 Kokkuvõte
- Viited
5.2 Normaaljaotus ja tema omadused
Teeme katse, kus viskame münti mitu korda (\(N\) korda), ja loendame, mitmel korral selles viskeseerias tuli “kull”. Teeme seda katset (loendame viskeseerias tulnud “kullide” arvu) näiteks 10946 korda. Seega saame justkui 10946 summat, kui summeerimisel loeme, et kiri = 0 ja kull = 1. Näiteks kui viskame 3 korda münti, millest kahel korral tuleb kull, siis selle viskeseeria summa on 2.
Allolevatel joonistel on kujutatud katsete tulemuste histogrammid erinevate viskeseeriate pikkuste \(N\) korral.
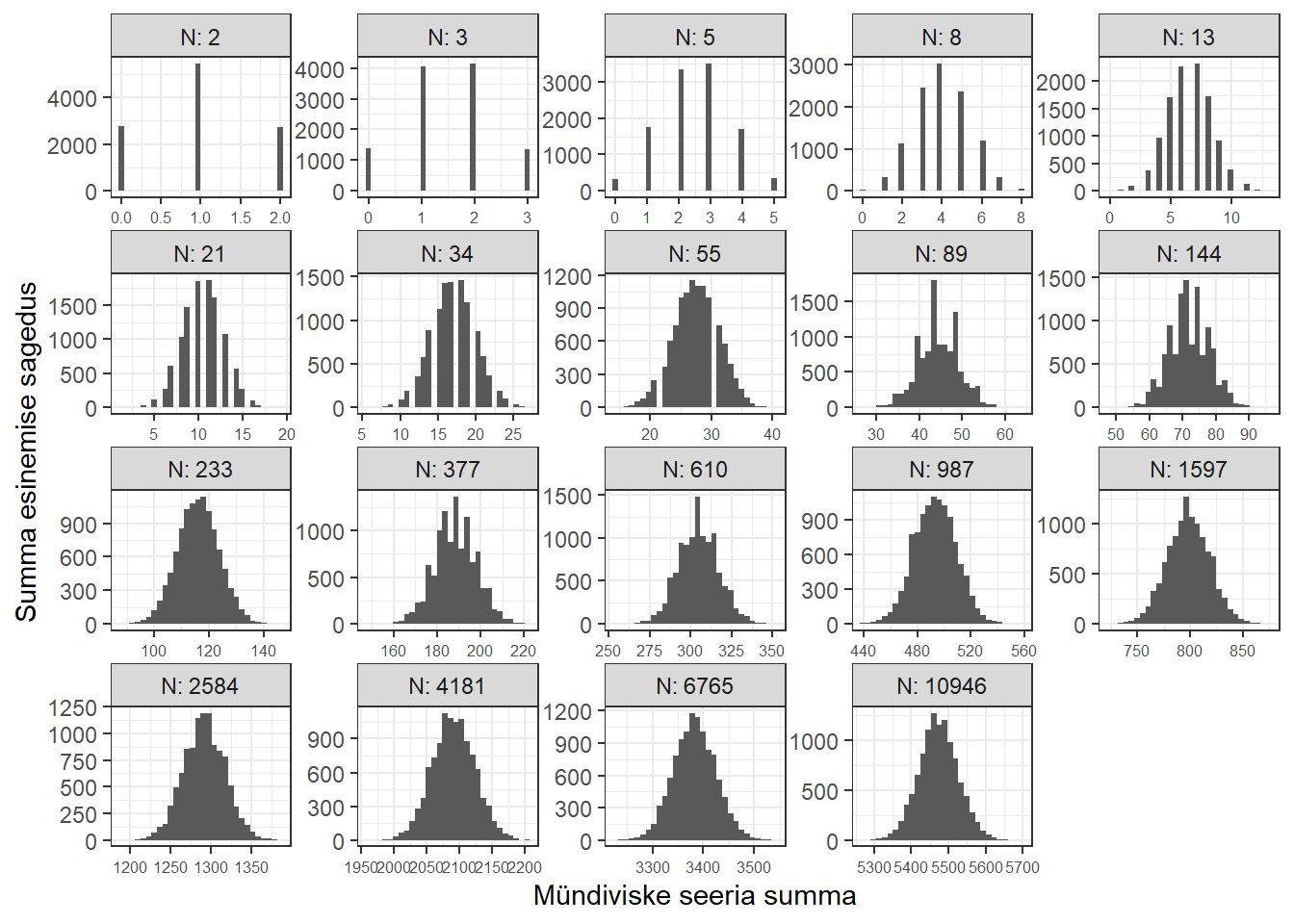
Nagu jooniselt näha, siis mida rohkem me münti viskame, seda nn siledamaks muutub mündiviske tulemuste summade histogramm (igal pildil on kokku 10946 viskeseeriat).
See jaotus, millele mündivisekeseeriate summade jaotus läheneb, on normaaljaotus.
Üksiku mündiviske tulemus (juhuslik suurus, \(x_i\)) on binaarne (kiri või kull). Iga mündivike tulemus on eelmisest sõltumatu, samas kõigil mündivisetel on kulli tulemise tõenoäsus sama. Praegu summeerisime üksikute mündivisete tulemused. Mida pikem oli viskeseeria (ehk mida suurem oli \(N\)), seda sarnasemkas muutus summade histogramm normaaljaotuse histogrammile. See on oluline tähelepanek. Nimelt:
Väide 5.1 Sõltumatute ja sama jaotusega juhuslike suuruste summa \(x_1+x_2+\dots+x_N\) jaotus ligineb normaaljaotusele, kui \(N\to\infty\).
See on mehhanism, kuidas nn looduses normaaljaotus tekib. Seda mehhanismi (sõltumatute sama jaotustega juhuslike suuruste summa jaotus koondub normaaljaotuseks) nimetatakse tsentraalseks piirteoreemiks (central limit theorem) ning see on teoreetilises statistikas üks olulisemaid tulemusi.
Paljud asjad päris-maailmas on mõjutatud üksteisest sõltumatute väga väikse mõjuga tegurite poolt. Näiteks inimese pikkust mõjutavad paljud geenid ning iga üksiku geeni mõju on väike, seepärast ongi pikkuse histogramm sarnane normaaljaotusega.
Vaatame lähemalt, mis see normaaljaotus täpsemalt on. Kui genereerida juhuslikke arve normaaljaotusest, millel teoreetiline keskmine (keskväärtus) on \(\mu\) (statistikažargoonis teoreetilisi arve ehk jaotuse parameetreid tähistatakse sageli kreeka tähtedega, valimi põhjal arvutatud statistikuid aga ladina tähtedega) ning teoreetiline standardhälve on \(\sigma\), siis selliste arvude histogramm on nn kellukesekujuline, nii et kellukese tipp asub x-teljel \(\mu\) kohal.
Samuti on pool histogrammist on keskväärtusest vasakul, pool paremal, järelikult nende arvude mediaan on samuti \(\mu\) – mediaan võrdub keskväärtusega.
Enamgi veel, see histogramm on sümmeetriline, st mistahes \(q\)-kvantiil, kus \(q < 0,5\), on mediaanist sama kaugel, kui tema vastandkvantiil \(1-q\). Näiteks ülal kõige viimasel väiksel histogrammil on 0,33-kvantiil (33. protsentiil) = 5449,99, mis on mediaanist (5473) sama kaugel, kui 0,67-kvantiil (67. protsentiil) = 5496,01. Ja näiteks 0,05-kvantiil (5386,96) on mediaanist sama kaugel kui 0,95-kvantiil (5559,04).
Tänu normaaljaotuse sümmeetrilisusele saab öelda, et vahemikku \(q\)-kvantiil kuni \((1-q)\)-kvantiil jääb mingi % kõigist väärtustest. Normaaljaotuse puhul on juhtumisi nii, et
- vahemikku \(\mu\pm\sigma\) jääb umbes 68% kõigist väärtustest (täpsemini u 68,3; 68,0% väärtustest jääb hoopis vahemikku \(\mu\pm 0,974\sigma\)),
- vahemikku \(\mu\pm 2\sigma\) jääb umbes 95% kõigist väärtustest (täpsemini u 95,4; 95% väärtustest jääb hoopis vahemikku \(\mu\pm 1,960 \sigma\)),
- vahemikku \(\mu\pm 3\sigma\) jääb 99,7% kõigist väärtustest (see on nii).
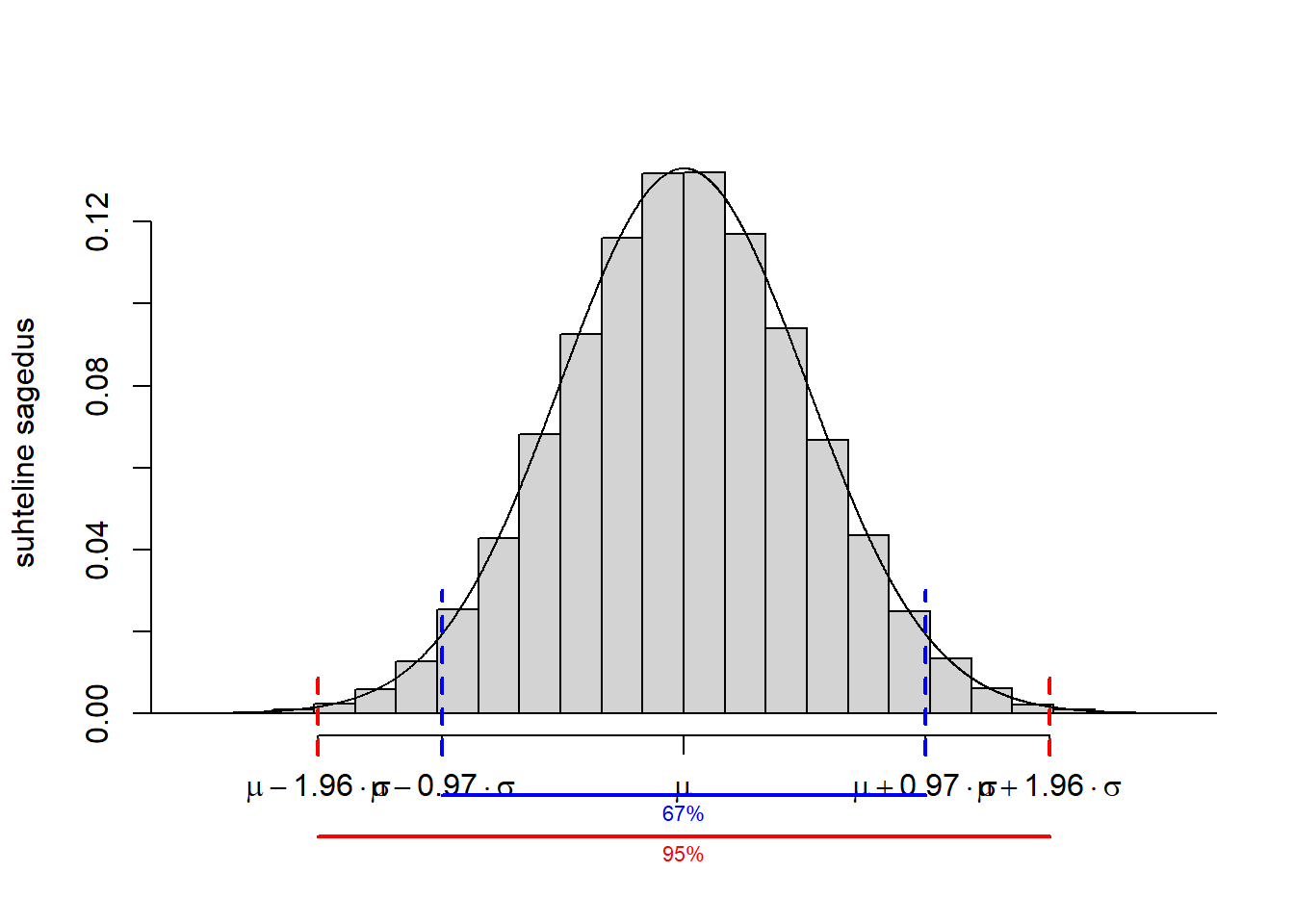
Joonis 5.1: Normaaljaotuse omadused
Normaaljaotuse jaotusfunktsioon
Teoreetilisi jaotuseid kirjeldatakse
tõenäosusfunktsiooniga, kui ei ole tegemist pideva arvulise tunnusega;
jaotusfunktsiooniga, kui on tegemist pideva arvulise tunnusega.
Näiteks mingi konkreetse ebaausa mündi viskamise puhul, kus mõlema külje maandumise tõenäosus on võrdne, saab tulemuse teoreetilist jaotust kirjeldada sellise jaotusfunktsiooniga: \[ P(X=x)=\begin{cases} 0,6 & \text{, kui }x=\text{'kull'}\\ 0,4 & \text{, kui }x=\text{'kiri'} \end{cases} \]
Samamoodi saab sobivate tõenäosusfunktsioonide (mis tegelikult loetlevad üles võimalikud variandid ning nende tõenäosused) abil ära kirjeldada kõigi mittepidevate tunnuste jaotused.
Pidevate arvuliste tunnuste puhul on asjalood natuke teised. Näiteks kui esitada juhuslikult valitud inimese pikkuse \(X\) kohta selline tõenäosuslik küsimus: \[P(X=174\text{ cm})=?,\] siis tuleb silmas pidada seda, et \(174=174,000000000000\dots\; .\)
Teisisõnu: proovige reaalarvude teljele noolt visates tabada lõpmatult täpselt mõnd reaalarvu sel teljel. See on võimatu, sest ühelgi punktil reaalarvude teljel pole suurust (st suurus on null). Samuti pole mitte ühelgi reaalarvude vektorruumi punktil suurust (näiteks kahemõõtmelises ruumis, kus mõlemad teljed (koordinaadid) koosnevad reaalarvudest.
Seepärast ei uurita pidevate arvuliste tunnuste puhul mitte punktide tõenäosuseid, vaid mingite arvuvahemike (intervallide) tõenäosuseid. Ehk siis sõnastatakse küsimus ümber: kui suur on tõenäosus, et inimene on vähemalt 174 cm pikk: \[P(X\leqslant174)=?\] Ehk siis: kui tõenäoline on, et pikkus on 174,000… cm, 173.999… cm (muide, 174,000… on tegelikult täpselt sama arv, mis 173,999…), või et pikkus on 173,999…9899… cm või 173,999…98999…8999… cm jne. Kõik need arvud paiknevad üksteisega lõpmatult tihedalt koos: iga kahe arvu vahel leidub alati veel üks arv.
Sellistes situatsioonides tuleb summa leidmiseks appi tema vend – integraal (muide, mõõduteoorias, mille alla tõenäosusteooria liigitub, kasutatakse tegelikult Lebesque’i, mitte Riemanni’i integraali).
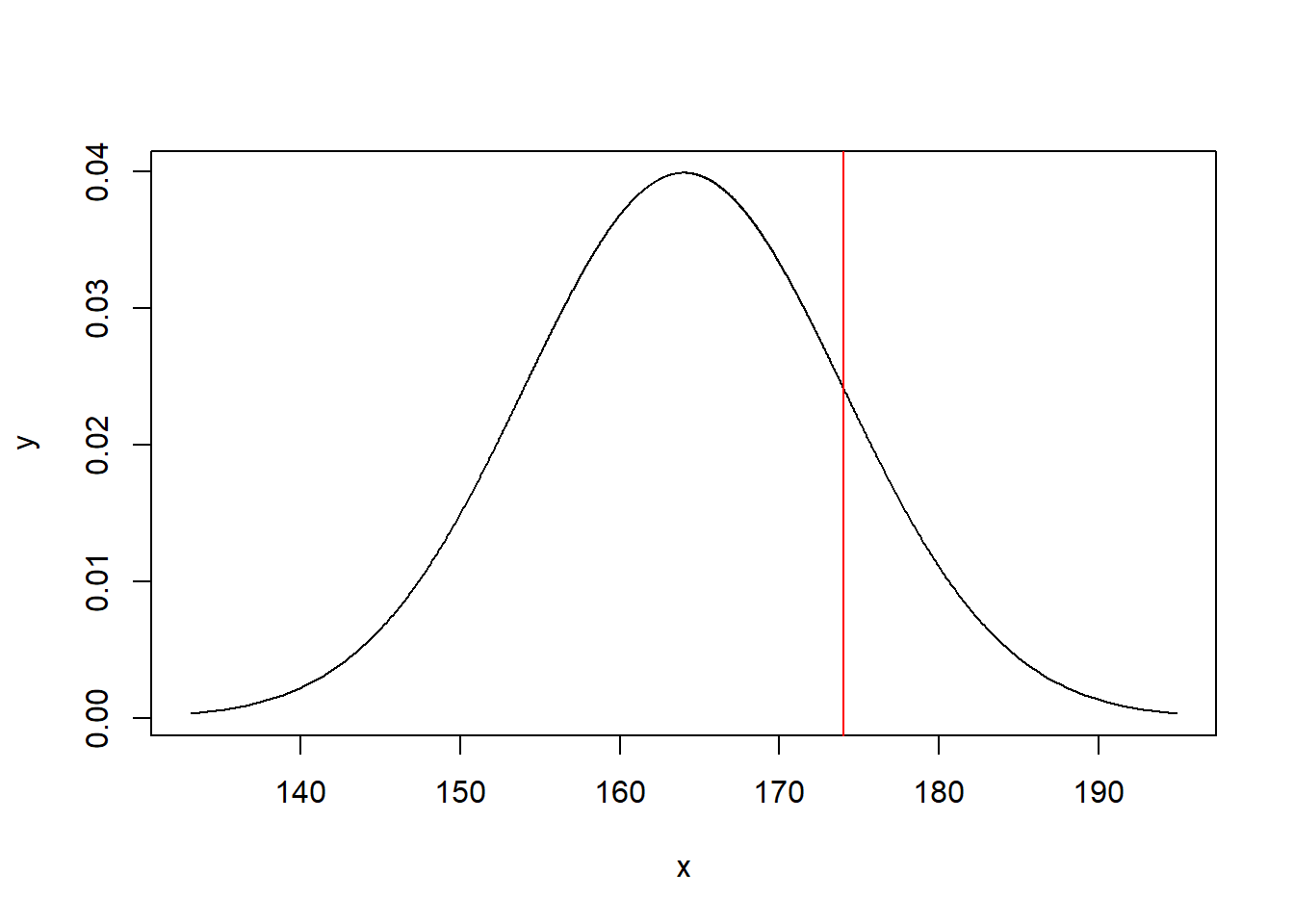
Pidevate tunnuste jaotumist defineerib tihedusfunktsioon (density function), mida enamasti tähistatakse väga originaalselt: \(f(x)\). Jaotusfunktsioon (distribution function), on tihedusfunktsiooni integraal: \[P(X\leqslant x)=\int_{-\infty}^{x}f(t)\text{d}t\]
Normaaljaotuse keskväärtusega \(\mu\) ja standardhälbega \(\sigma\) puhul on tihedusfunktsioon \[f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{\mu - x}{\sigma}\right)^2}\] See ongi see kellukesekujuline kõver, mida enamasti normaaljaotust kujutavatel joonistel näha on.