- Eessõna
- 1 Sissejuhatus
- 2 Tõenäosus
- 3 Diagnostilised testid
- 4 Kirjeldav statistika
- 5 Statistilised hinnangud
- 6 Statistiline hüpoteeside testimine
- 6.1 Ühe valimi z-testi ja t-testi eeldused
- 6.2 z-test protsendi võrdlemiseks konstandiga
- 6.3 I ja II liiki viga
- 6.4 Mõned lihtsamad statistilised testid
- 6.4.1 Ühe valimi z-test (1 keskväärtus või 1 protsent)
- 6.4.2 Ühe valimi t-test (1 keskväärtus)
- 6.4.3 Märgitest (1 protsent)
- 6.4.4 Kahe sõltumatu valimi z-test (2 keskväärtust või 2 protsenti)
- 6.4.5 Kahe sõltumatu valmi t-test (2 keskväärtust)
- 6.4.6 Wilcoxoni astaksumma test (2 mediaani*)
- 6.4.7 Paarisvaatluste t-test (keskväärtus enne ja pärast)
- 6.4.8 Wilcoxoni astakmärgitest (mediaan enne ja pärast*)
- 6.4.9 hii-ruut test (mitu protsenti)
- 6.4.10 Fisheri täpne test (mitu protsenti*)
- 6.4.11 Bartletti test (mitu protsenti*)
- 6.4.12 McNemari test (protsent* enne ja pärast)
- 6.4.13 F-test ja ANOVA
- 6.4.14 Kruskal-Wallise astaksumma test (mitu mediaani*)
- 6.4.15 Shapiro-Wilki test (normaaljaotuse kontrollimine)
- 6.4.16 Permutatsioonitest (universaalne*)
- 6.5 Mitmene võrdlemine
- 6.6 Ühepoolsed testid
- 7 Korrelatsioon
- 8 Regressioonanalüüs
- 9 Elukestusanalüüs
- 10 Kokkuvõte
- Viited
5.3 Usaldusvahemik
Eelnevalt sai demonstreeritud, kuidas juhuslike arvude (sõltumatud, samast jaotusest) summa järgib normaaljaotust (kui neid arvusid / liidetavaid on piisavalt palju). Tegelikult väidab tsentraalne piirteoreem isegi enamat: nende arvude (juhusliku suuruse realisatsioonide) aritmeetiline keskmine (\(\bar x = \sum_{i=1}^{N}x_i\)) järgib normaaljaotust, millel on sama keskväärtus, kui sellel juhuslikul suurusel.
Võtame näiteks 2001.–2020. a 2. kursuse arstitudengid. Nende kehamassiindeksid on jaotunud selliselt:
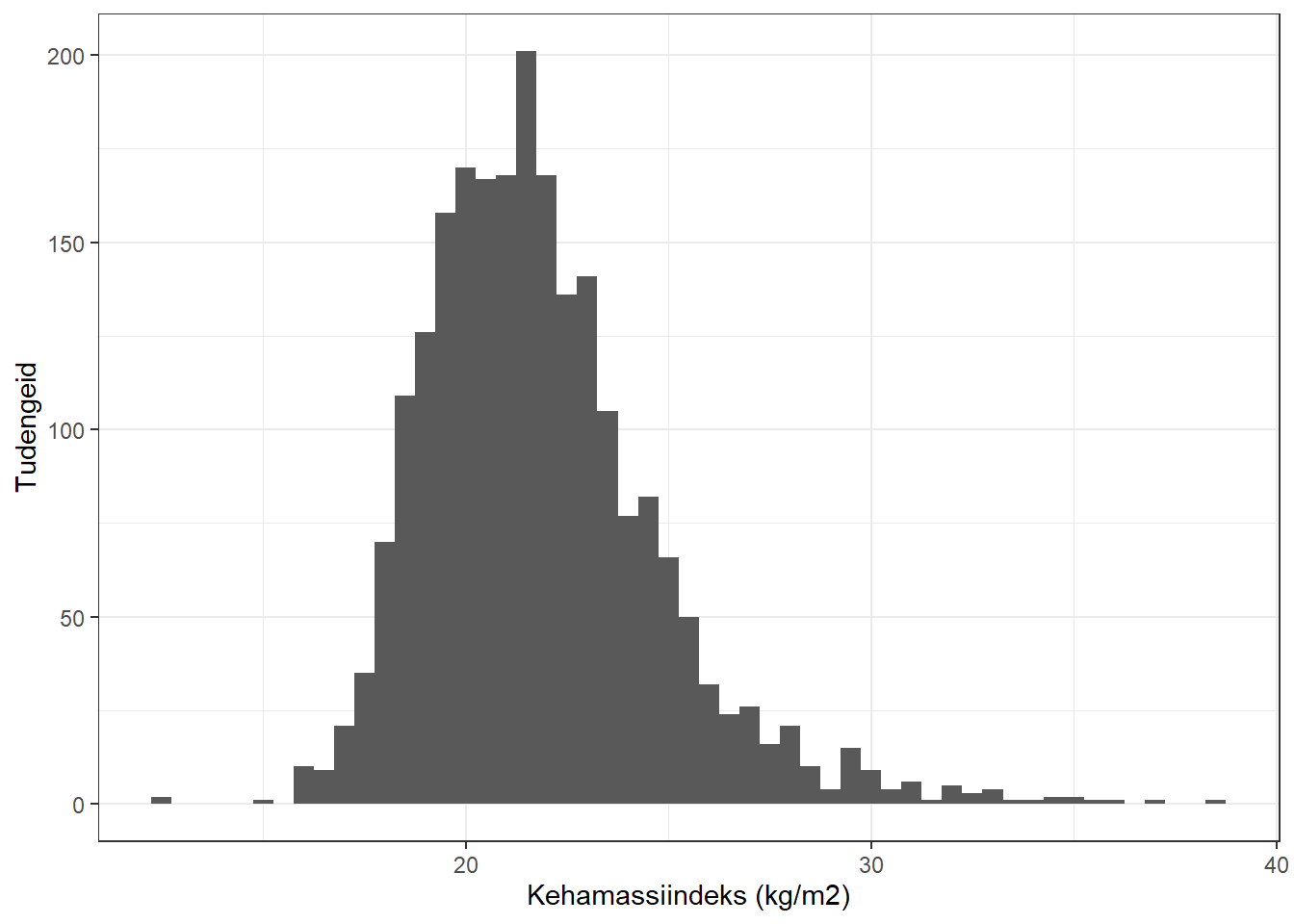
Nagu näha, siis see jaotus on üsna ebasümmeetriline: parempoolne nn saba on palju paksem ja pikem kui vasakpoolne. Keskmine KMI on selles rahvastikurühmas 21,83. Võtame sellest hulgast 200 tudengiga juhuvalimi, sellises valimis tuleb keskmine KMI 22,01. Võtame sellest populatsioonist uuesti juhuvalimi 100 tudengiga, selle valimi keskmine tuleb 22,34. Kordame seda valimi võtmist ja keskmise arvutamist 3000 korda.
Alloleval joonisel on järjestikuste katsete tulemused, punase joonega on kujutatud üldkogumi (2001-2020 arstitudengid teiselt kursuselt) tegelik keskmine KMI. Sellele järgneval joonisel on kujutatud katsetulemuste jaotus.
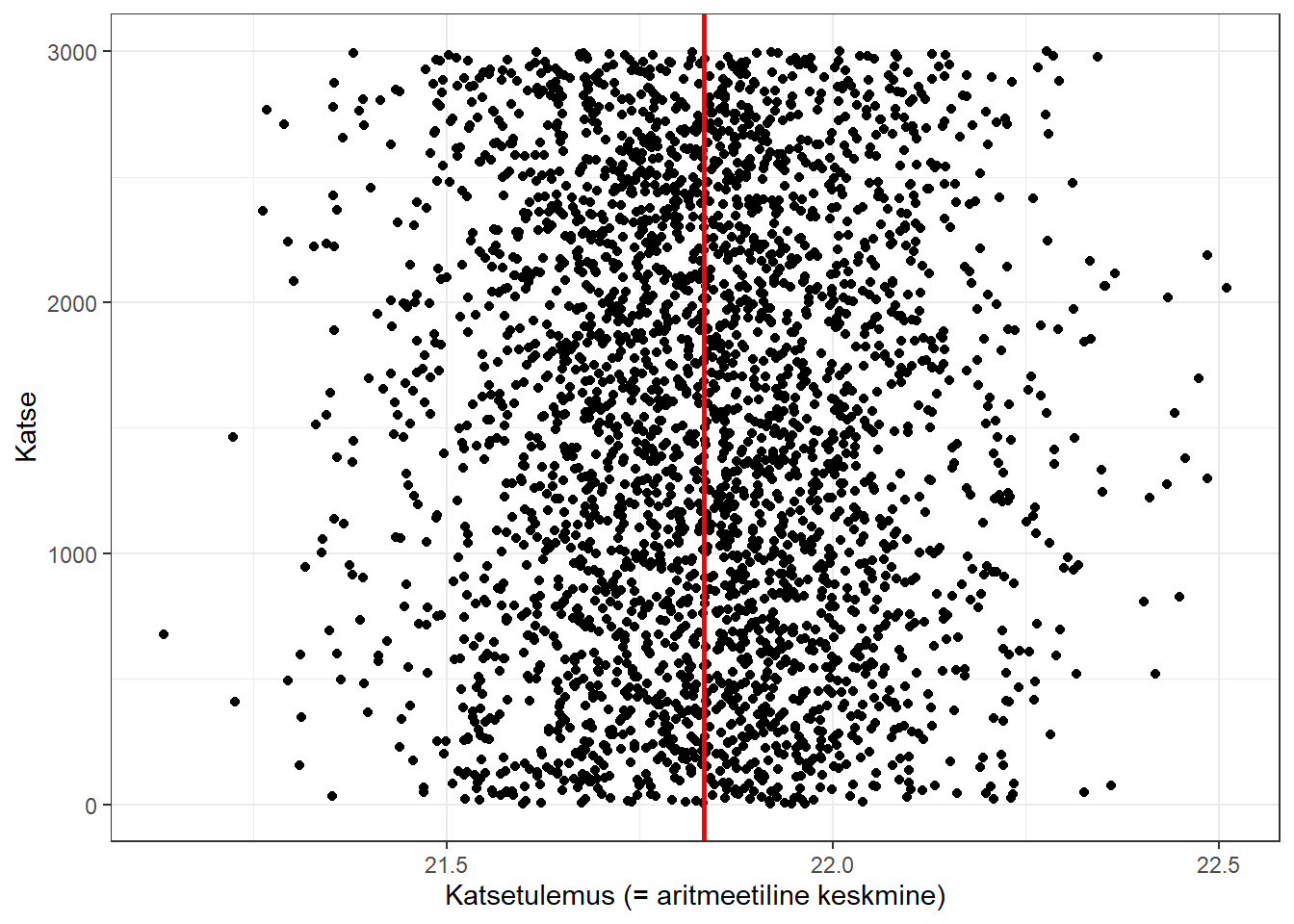
Joonis 5.2: Juhuvalimist saadud aritmeetilised keskmised katsete kaupa
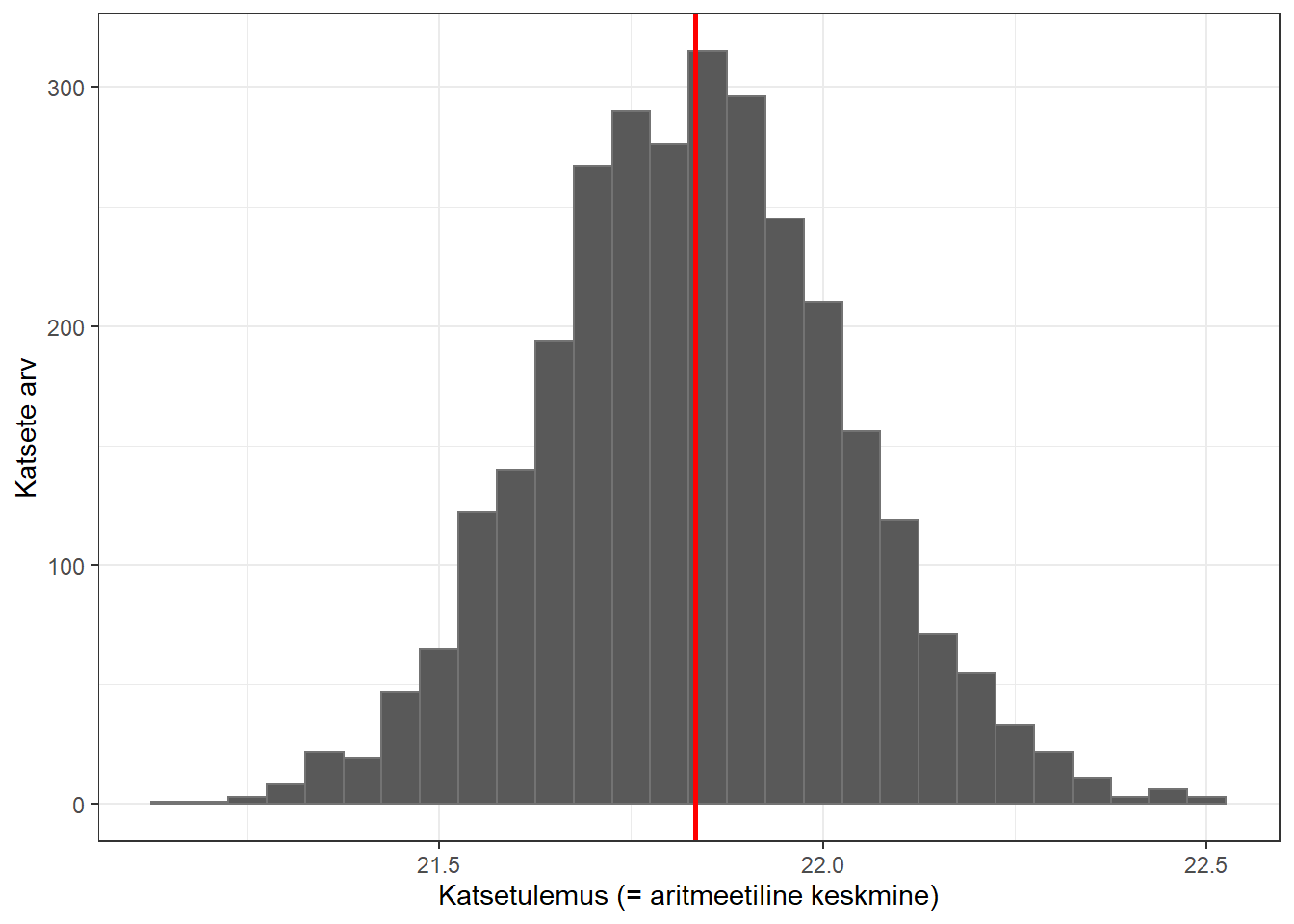
Joonis 5.3: Katsetulemuste jaotus
Nagu näha, siis valdav osa katsetulemusi tuli tegeliku keskmise KMI lähedale; teatav osa tuli keskmisest natuke kaugemale ning üsna väike osa hälbis tegelikust keskmisest KMIst märgatavalt. Neis 3000 katses arvutatud katsetulemuste (aritmeetiliste keskmiste) põhjal arvutatud aritmeetiline keskmine on 21,83, standardhälve on 0,20. Seda – lõpmatult paljude katsete tulemuste – standardhälvet nimetatakse standardveaks.
Hinnatav statistik on meil praegu KMI keskväärtus (st üldkogumi tegelik aritmeetiline keskmine KMI); kuna me tegime hästi palju katseid, siis seetõttu nende katsete põhjal hinnatud standardviga (kõigi katsetulemuste põhjal arvutatud standardhälve) on üsna lähedal tegelikule ehk teoreetilisele standardveale.
Kõigist 3000 katsetulemusest oli 69,3% keskmisest katsetulemusest mitte kaugemal kui 1 standardviga, 95,3% aga mitte kaugemal kui 2 standardviga.
Järelikult: piisavalt suure valimiga tehtud katsete tulemused järgivad normaaljaotust, mille keskväärtus on üldkogumi tegelik keskväärtus.
Teisisõnu, kui me teeme ühe uuringu (ehk katse; nt ühe valikuuringu või siis ühe kliinilise katse), siis me teame seda, et uuringuga saadud tulemus tõenäoliselt on tegelikule huvipakkuvale parameetrile (nt üldkogumi keskmisele) üsna lähedal. Sealjuures u 95%-lise tõenäosusega ei ole selles uuringus saadud tulemus nn õigest väärtusest kaugemal kui 2 x standardviga.
AGA: kui me teeme ühe ühe uuringu, siis on meil ju vaid üks uuringutulemus, mitte näiteks 3000 erineva uuringu tulemust, mille põhjal standardviga (uuringutulemuste standardhälvet) arvutada. Õnneks on tõenäosusteooriast teada, et üksikute mõõtmistulemuste standardhälbe ning mõõtmistulemuste arvu (valimi suuruse) ruutjuure suhe on hea hinnang standardveale: \[SE = \frac{s}{\sqrt{n}}\] Väga tore! Seega ei pea tegema mitut uuringut, et teada saada, kui kaugel ühe uuringu tulemus võib nn õigest väärtusest olla. 95%-lise tõenäosusega uuringust saadud aritmeetiline keskmine \(\bar{x}\) ei ole tegelikust üldkogumi keskmisest (\(\mu\)) kaugemal kui \(2 \times \frac{s}{\sqrt{n}}\) (tegelikult \(1,96\times\frac{s}{\sqrt{n}}\)).
Teisisõnu: võime 95% kindlad olla, et vahemik \[\bar{x} \pm 1,96 \times \frac{s}{\sqrt{n}}\] sisaldab üldkogumi tegelikku keskmist \(\mu\). Seda vahemikku nimetatakse 95-protsendiliseks usaldusvahemikuks keskväärtusele.
Definitsioon 5.2 95%-line usaldusvahemik on arvuvahemik, mis hinnatavat üldkogumi parameetrit sisaldab 95%-lise tõenäosusega.
\(p\)%-line usaldusvahemik (confidence interval, CI) on vahemik, mis hinnatavat üldkogumi parameetrit sisaldab \(p\)%-lise tõenäosusega.
Usaldusvahemiku piire kutsutakse alumiseks ja ülemiseks usalduspiiriks (lower/upper confidence limit).Võimalusi, kuidas rehkendada taolist arvuvahemikku, mis etteantud tõenäosusega
meile huvipakkuvat üldkogumi parameetrit sisaldaks, on mitmeid. Eelpool tutvustatud
varianti
\[parameeter \pm 1,96 \times SE\]
nimetatakse Waldi-tüüpi (95%liseks) usaldusvahemikuks;
seda saab kasutada vaid olukorras, kus huvipakkuva parameetri hinnang allub
normaaljaotusele. Keskväärtuse hinnang – aritmeetiline keskmine – seda õnneks teeb.
Ega üksiku uuringu puhul me ju tegelikult ei tea, kas 95%-line usaldusvahemik ka päriselt õiget keskväärtust sisaldab. Nende 3000 katse puhul, kus valiti kõigi 2001–2020 arstitudengite hulgast igas katses 200 inimest, juhtus 141 korral nii, et 95%line usaldusvahemik ei katnud tegelikku keskväärtust ära.
Alloleval joonisel on kujutatud katsete nr 668 kuni 687 tulemusi (keskväärtuse hinnang (aritmeetiline keskmine) koos 95%lise usaldusvahemikuga).
Joonis 5.4: Mõnes katses saadud keskväärtuse hinnangud koos 95% usaldusvahemikuga
Katses nr 678 on saadud tulemus, mis on õigest üldkogumi keskväärtusest (punane) üsna kaugel, sealjuures ka usalduspiirid jäävad õigest väärtusest üsna kaugele. Tasub tähele panna, et selles katses on usaldusvahemik märksa kitsam (ÜUP - AUP = 0,69), kui paljud teised sel joonisel olevad usaldusvahemikud. Järelikult: kui usaldusvahemik on üsna kitsas, siis ei pruugi see tähendada, et hinnang on tõesele väärtusele lähedal.
Kuidas soodustada seda, et uuringus saadud hinnang oleks tõele lähedal? Kõige olulisem – valida õige uuringukavand ning uuring korralikult planeerida. Järgmine samm: võtta üldkogumist võimalikult suur valim. Mida suurem on valim, seda suurem on tõenäosus, et uuringu tulemus on tõele lähedal.
Alloleval joonisel on kujutatud tudengite KMI hinnang koos 95%lise usaldusvahemikuga erinevate valimisuuruste korral. Tõepoolest, keskväärtuse hinnang (punkt usaldusvahemiku keskel) on seda lähemal õigele keskväärtusele, mida suurem on valim.
Tasub tähele panna, et kõige suurem valim, kuhu oli kaasatud kogu üldkogum (kõikne valim) – selle valimi puhul on usaldusvahemiku laius 0. Tõepoolest, kui on tegemist kõikse valimiga (kus puuduvaid väärtuseid pole), siis pole vajadust mingisuguseks peeneks arvutuseks usaldusvahemike saamiseks, sest üldkogumi parameetrid on täpselt teada.
Joonis 5.5: Erineva suurusega valimist saadud 95% usaldusvahemikud keskväärtusele
ehk 21,7 kuni .
Kui valimisse kaasatakse oluline osa lõplikust üldkogumist (nt valikuuring kaasab
10% või suurema osa rahvastikust), siis on vaja arvesse võtta seda asjaolu,
et üldkogum pole lõpmatult suur. Kuidas?
Tegemist on eelkõige valikuuringute teooriat puudutava küsimusega. Kui tegemist
on lihtsa juhuvalikuga ilma tagasipanekuta (st et üht inimest kaasatakse valimisse
vaid ühe korra), siis keskväärtuse hinnangu puhul on seda üsna lihtne teha:
usaldusvahemiku laius ei ole mitte standardvea-kordne, vaid standardviga tuleb
koefitsiendiga
\[\sqrt{\frac{N-n}{n-1}}\]
läbi korrutada (siin \(N\) on üldkogumi suurus ning \(n\) on valimi suurus). Näiteks
kui tudengeid on üldkogumis kokku 2262 ning valimi suurus on 1484 ja
selles valimis saadi keskmine KMI 21,82 standardhälbega 2,10, siis
95% usaldusvahemik on
\[\bar{x} \pm 1,96 \times \frac{s}{\sqrt{n}} \times \sqrt{\frac{N-n}{n-1}}\\= 21,82 \pm 1,96 \times \frac{ 2,10 } {\sqrt{ 1484 }} \times \sqrt{\frac{ 2262 - 1484 }{ 1484 -1}}\]
Kui vaadata keskväärtuse hinnangu standardvea hinnangut (\(SE = \frac{s}{\sqrt{n}}\)), siis on selge, et lisaks valimi suurusele \(n\) mõjutab usaldusvahemiku laiust ka valimis nähtav standardhälve \(s\): mida varieeruvamad on valimis mõõtmistulemused, seda suurem on nende põhjal hinnatud keskväärtuse standardviga. Ent nagu ülalt jooniselt 5.4 oli näha (seal olid kõik valimid sama suured, seega 95% usaldusvahemiku laiuse määras vaid standardhälve) ei pruugi väiksem standardhälve tähendada seda, et uuringus saadud hinnang on üldkogumi parameetrile lähedal.
Kui vaadata Waldi usaldusvahemiku arvutamise valemit \[hinnang \pm kordaja \times SE,\]
siis on selge, et lisaks standardveale (mida mõjutavad valimi suurus ja mõõtmistulemuste standardhälve) mõjutab usaldusvahemiku laiust ka see kordaja, millega standardviga läbi korrutatakse. Kust see kordaja tuleb?
Nagu teada, siis normaaljaotuse puhul 95% kõigist väärtustest jääb vahemikku \(keskväärtus \pm 1,96 \times standardhälve\) (kui meie mõõtmistulemuseks on üldkogumi mingi parameeter, siis standardhälvet nimetatakse standardveaks) ning 90% kõigist väärtustest jääb vahemikku \(keskväärtus \pm 1,64 \times standardhälve\).
Näiteks sellisel normaaljaotusel, millel keskväärtus \(\mu = 0\) ning standardhälve \(\sigma = 1\), jääb 90% kõigist väärtustest vahemikku -1,64…1,64. Sellist normaaljaotust, mille keskväärtus on 0 ning standardhälve on 1, nimetatakse standardnormaaljaotuseks (standard normal distribution).
Kuna standardnormaaljaotuse keskväärtus on 0 ja standardhälve 1, siis järelikult vahemikku \(0 \pm 1,96 \times 1\) ehk \(-1,96 \ldots +,96\) jääb sellel jaotusel 95% kõigist väärtustest. Järelikult need arvud, \(-1,96\) ja \(+1,96\) on standardnormaaljaotuse 0,025- ning 0,975-kvantiilid (ehk 2,5. ja 95,5. protsentiil). Niisiis on hea, kui Waldi-tüüpi usaldusvahemiku arvutamisel on käepäerast tabel standardnormaaljaotuse kvantiilidega. Kuna standardnormaaljaotus – nagu iga muugi normaaljaotus – on sümmeetriline, siis tema kvantiilid asuvad mediaanist (0) võrdsel kaugusel. Seega piisab vaid sellest, kui teame pooli kvantiile (nt mediaanist suuremaid kvantiile); ülejäänud pool on samad, aga vastupidise märgiga.
| p%-line UV | Mitmes kvantiil? | Kvantiili väärtus (SE kordaja) |
|---|---|---|
| 20 | 0,600 | 0,2533 |
| 40 | 0,700 | 0,5244 |
| 60 | 0,800 | 0,8416 |
| 70 | 0,850 | 1,0364 |
| 80 | 0,900 | 1,2816 |
| 90 | 0,950 | 1,6449 |
| 95 | 0,975 | 1,9600 |
| 98 | 0,990 | 2,3263 |
| 99 | 0,995 | 2,5758 |
Joonis 5.6: Standardnormaaljaotuse kvantiilid (tihedusfunktsioon)
Joonis 5.7: Standardnormaaljaotuse kvantiilid (jaotusfunktsioon)
Kuna see omadus, et vahemik \(\mu \pm z_q \times \sigma\) (kus \(z_q\) on q-nda kvantiili väärtus, \(q<0,5\)) sisaldab \(1-2q\) osa kõigist normaaljaotuse väärtustest – see omadus kehtib kõigi normaaljaotuste puhul, siis piisab sellest, kui teame standardnormaaljaotuse kvantiile. Kasutades neid standardhälbe kordajatena, teame seeläbi kõigi normaaljaotuste kvantiile.