4 Kirjeldav statistika

Mida võiks järeldada järgmisele tabelile peale vaadates?

Üsna mitte midagi. Ühe-kahe isiku vastuseid vaadates oleme neid võimelised eritlema, ent nende põhjal üldistusi teha on raske. Rohkemate andmete pealt aga inimsilm ja -aju pole harjunud kiiresti üldistusi tegema. Seepärast ongi andmete kompaktseks esitamiseks kasutusel statistikud.

Definitsioon 4.1 Statistik on valimi põhjal arvutatud arvnäitaja.

Tuntumad statistkud on osakaal (%), keskmine, standardhälve, miinimum, maksimum, mediaan. Millist statistikut sobib kasutada, sõltub aga tunnuse (juhusliku suuruse) tüübist.

4.1 Tunnuste tüübid

Tõenäosusteoorias jaotatakse tunnuseid kaheks:

pidevad – arvulised, teoreetiliselt lõpmatult täpselt mõõdetavad tunnused; näiteks pikkus – saab mõõta 1 m täpsusega \(10^{-5}\) m täpsusega, \(10^{-500}\), \(10^{-5\cdot10^{10}}\) jne m täpsusega, kui vaid on piisavalt täpsed mõõtmisvahendid;
mittepidevad ehk diskreetsed – kõik, mis ei ole pidevad.

Rakenduslikus statistikas võib mittepidevad tunnused veel jaotada alamliikideks:

arvulised diskreetsed tunnused – täisarvuga mõõdetavad tunnused (nt laste arv peres: 0, 1, 2, 3, …. (teoreetiliselt \(\infty\)), liiklusõnnetuste arv päevas, tudengite arv praktikumis, inimese vanus (tegelikult ei pea seda allapoole täisaastaks ümardama), haiglas olevate inimeste arvu muutus: …, -20, -19, …, -2, -1, 0, 1, 2, …, 19, 20, …);
mittearvulised ehk kvalitatiivsed tunnused:
- järjestustunnused ehk ordinaartunnused – tunnused, mille väärtute vahel on loomulik järjekord; näiteks haridustase (alg, põhi, kesk+), vanusrühm (0-19, 20-39, 40-45, 46+ aastat);
- nominaaltunnused – tunnused, mille väärtuste vahel ei ole loomulikku järjekorda; näiteks elukoha maakond (saab järjestada tähestiku, rahvaarvu, pindala jne järgi, aga kõik need on üsna arbitraarsed valikud), juuksevärv
  - mittejärjestatavate tunnuste oluline alamliik on kaheväärtuselised ehk binaarsed ehk dihhotoomsed tunnused – sellised tunnused, millel on vaid kaks erinevat väärtust võimalikud: mündiviske tulemus (kui on tegemist mündiga, mis servale seisma ei jää), jah/ei küsimuste vastused, sugu (tavainterpretatsioonis)

Tunnuste jaotus

Tasub tähele panna, et kui vanust on mõõdetud täpselt, on tegemist pideva tunnusega, kui aga täisaastates, siis diskreetse tunnusega. Tihti küsitakse küsitlusuuringus inimeste sissetulekut mitte täpse arvuna, vaid vahemikuna. Taolised mõõtmistulemused on aga mittearvulised, sest tegemist on vahemike/kategooriatega, palgavahemike näites on tegemist järjestustunnusega. Niisiis tunnuse tüüp sõltub eelkõige sellest, kuidas seda mõõdetakse.

Mõnikord on arvulisel tunnusel väga vähe erinevaid väärtuseid ja ülekaalukalt suur osa väärtustest on kuhjunud üsna üksteise lähedale. Näiteks kui küsitletakse põhikooli 1. klassi lapsi ning vastajate vanused on (täisaastates mõõdetuna) 6 ja 7 aastat, siis sellises olukorras võib vanust hoopis analüüsida samadel põhimõtetel, nagu binaarset tunnust. Samuti kui 2. kursuse arstitudengid on valdavalt 19, 20 ja 21 aastat vanad ning on vaid väga üksikuid kes on üle 21 aasta vana, on mõistlik vanus rühmitada neljaks kategooriaks (19, 20, 21, 22+) ning kasutada neid meetodeid, mida järjestustunnuste puhul kasutatakse.

Kui andmed on kogutud ja analüüsitavaks korrastatud, siis järgmine samm on andmete kontrollimine – võimalike sisestusvigade leidmine ja parandamine – ning andmetest esmase ülevaate saamine. Andmeid saab kirjeldada nii arvuliselt – tabelite ja kirjeldavate statistikute abil – kui ka graafiliselt. Milline kirjeldusviis on kõige sobilikum, sõltub tunnuse tüübist.

4.2 Kirjeldavad statistikud

Nagu eelnevalt mainitud, sõltub tunnuse tüübist väga palju, mil moel andmeid kirjeldada ja analüüsida.

Binaarset tunnust sobib kõige paremini kirjeldada osakaalu ehk protsendiga ning sagedusena (nn tükkide arvuna). Tihti piisab vaid ühe väärtuse osakaalu mainimisest, sest kaks väärtust kokku annavad 100% (nt: 2. kursusel on mehi 34% – järelikult naisi on 66%).

Sagedustabelit pelgalt selle ühe binaarse tunnuse jaotumise kohta ei ole mõtet teha, sest see võtab palju rohkem ruumi, kui pool lehekülge samasisulist lauset. Samal põhjusel ei ole vääri lehekülje ruumi ka binaarse tunnuse kohta tehtavad joonised. Kui aga mingis ettekandes või esitluses on ilmtingimata väga-väga vältimatult vaja binaarse tunnuse jaotust esitada, siis on soovitatav kasutada selleks tulpasid (nt tulpdiagramm), mitte aga jooniseid, mille tõlgendamisel tuleb lähtuda pindalast või nurgast. Nimelt on teaduslikult tõestatud, et inimslim suudab lihtsamini eristada kauguseid/pikkuseid kui nurkade suuruseid või alade pindalasid¹⁴.

Ka teisi mittearvulisi tunnuseid sobib eelkõige kirjeldada osakaalude abil; tihti kasutatakse selleks jaotustabeleid – tabeleid, kus lahtrites on vastavate kategooriate osakaalud. Tabeleid, kus protsentida asemel on objektide arvud ehk sagedused, nimetatakse sagedustabeliteks. Tihti on sagedus- ja jaotustabel kombineeritud.

Tabel 4.1: Seltskondlikest üritustest osavõtmise suhtelise sageduse hinnang 2020. a 2. kursuse arstitudengite hulgas
	Vastajaid	Osakaal (%)
Palju harvem kui enamik eakaaslasi	12	8.96
Harviemini kui enamik eakaaslasi	50	37.31
Umbes sama tihti kui enamik eakaaslasi	56	41.79
Sagedamini kui enamik eakaaslasi	13	9.70
Palju sagedamini kui enamik eakaaslasi	3	2.24

Mittearvulise tunnuse jaotuseks on sobilik kasutada ka tulpdiagrammi (barplot) – joonist, kus ühel teljel on kategooriad ning teisel teljel kas sagedused või osakaalud. Rõhutamaks, et tegemist ei ole pideva tunnusega, on tulpdiagrammil tulpade vahel vahed.

Mõnikord kasutatakse mittearvuliste tunnuste kirjeldamiseks ka muid jooniseid, näiteks sektordiagrammi. Nagu eelpool mainitud, siis inimese silm oskab kõige paremini eristada pikkuseid, märksa vähem nurki või pindalu. Näiteks sektordiagrammi, kus ei ole täiendavat annotatsiooni, põhjal mingi kategooria osakaalu hinnates on hinnangud palju ebatäpsemad, kui tupldiagrammi põhjal.

Ja mitmesugused muud eksootilisemad joonistused on pahatihti veelgi eksitavamad, vt nt https://stat24.ee/2015/02/kuidas-statistika-abil-valetada-valimiste-eri/

Arvuliste tunnuste kirjeldamiseks leidub terve plejaad statistikuid.

Miinimum ja maksimum on kasvavalt järjestatud arvrea vastavalt kõige esimene arv ja kõige viimane arv. Näiteks arvrida 66.7, 26.48, 69.68, 52.37, 10.23 on kasvavalt järjestatuna selline: 10.23, 26.48, 52.37, 66.7, 69.68. Miinimum on 10.23 ning maksimum 69.68.

Haare \(=\text{maksimum} - \text{miinimum}\). Nende viie arvu puhul on haare 59.45. Haare kirjeldab, seda kui suures vahemikus arvud esinevad / varieeruvad.

Kvantiilid ehk protsentiilid – järjestatud arvrea 0,2-kvantiil ehk 20. protsentiil on selline koht selles reas, millest väiksemad arvud moodustavad 20% selle arvrea arvudest. Nende arvude näites on 0,2-kvantiil = 18.355. Tasub märgata, et kvantiil ei pruugi ise üldse selle arvrea arv olla – ja ei peagi: kvantiili eesmärk on jaotada arvrida. Samuti tasub teada, et kvantiilide arvutamise meetodeid on küllalt palju ning erinevad tarkvarad kasutavad erinevaid lähenemisi¹⁵. Seepärast ei maksa ehmuda, kui teadlasest kolleegi artikli käsikirjas on näiteks 0,25-kvantiili väärtus õige natuke teistsugune, kui sinul endal oli arvutatud. Lisaks võimalikule arvutusveale tasub üle kontrollida ka see, et on sama meetodit kasutatud. See on ka üks põhjustest, miks tänapäeval aina rohkem on teadusartiklites ka mainitud, millist tarkvara on andmete analüüsimiseks kasutatud.

Kvartiilid: 1. 2. ja 3. kvartiil on 0,25-, 0,50- ja 0,75-kvantiilid – need jaotavad järjestatud arvrea neljaks võrdse suurusega (arvude hulgaga) osaks. Viie arvuga näites on need vastavalt 26.48, 52.37 ja 66.7. Kvartiilid ei ole kuigivõrd tundlikud selle suhtes, kui arvritta mõni üksik arv juurde lisandub või muutub.

Mediaan on 2. kvartiil ehk 0,5-kvantiil ehk 50. protsentiil.

Kvartiilide haare (IQR, interquartile range) \(= \text{3. kvartiil} - \text{1. kvartiil}\). Näidet jätkates on see eelmainitud 5 arvu põhjal 40.22. Kvartiilide haare näitab, millises vahemikus paikneb keskmine osa vaadeldavatest väärtustest.

Mood on selline arv, mida arvrea esineb kõige sagedamini. Jooksvas viie arvuga näites on kõik arvud kõige sagedasemad (sagedus = 1), seega on tegemist nn multimodaalse (mitme moodiga) arvreaga.

Aritmeetiline keskmine (arithmetic mean) on statistikas kõige rohkem kasutatav statistik, enamasti jäetakse täiend “aritmeetiline” eest ära. Valimi põhjal arvutatud aritmeetilist keskmist tähistatakse enamasti \(\bar{x}\): kui on mingid arvud \(x_1, x_2, x_3, \dots, x_n\) (näiteks needsamad 5 arvu: \(x_1=66.7, x_2=26.48, x_3=69.68, x_4=52.37, x_5=10.23\)), siis nende aritmeetiline keskmine on nende arvude summa jagatud nende koguarvuga: \[\bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n}\] ehk summa märki (suur kreeka sigma täht) kasutades (valemi järel olev punkt on lauset lõpetav punkt): \[\bar{x} = \frac{1}{n} \sum_{i = 1}^{n} x_i\;\;.\] Dispersioon (variation) iseloomustab keskmist üksikute arvude ruutkaugust valimi keskmisest ja arvutatakse nii:
\[\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2\;\;.\] Kui tunnus on mõõdetud mingi ühikuga (nt cm), siis dispersiooni puhul on ühikuks vastav ruut (nt cm²).

Standardhälve (standard deviation) on ruutjuur dispersioonist, valimi põhjal arvutatud standardhälvet tähistatakse sageli tähega \(s\): \[s = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2}\]

Üks põhjustest, miks teadusartiklites esitatakse sagedamini standardhälvet kui dispersiooni on see, et standardhälbe ühik on sama, mis uuritaval tunnusel (nt cm).

Nii dispersioon kui ka standardhälve iseloomustavad, kui hajusalt paiknevad andmed (tunnuse üksikud väärtused) aritmeetilise keskmise ümber. Kui standardhälve on (mõõtmisskaalaga võrreldes) väike, on mõõdetud väärtused kontsentreerunud keskväärtuse lähedale. Kui standardhälve on suur, siis mõõdetud väärtused on väga erinevad (vähemalt üks on teistest väga erinev)

Standardhälbe ja aritmeetilise keskmise suhet nimetatakse suhteliseks standardveaks ehk variatsioonikordajaks (coefficient of variation). Variatsioonikordaja iseloomustab, kas kesväärtuse hinnang on pigem täpne või ebatäpne. Nt elevantide keskmise kaalu arvutamisel võib standardhälve olla \(s = 120 \text{ kg}\), laborihiirte keskmise kaalu puhul aga \(s = 1,5 \text{ g}\). Ent kui elevantide keskmine kaal on \(x = 7000 \text{kg}\) ja laborihiirte keskmine kaal on 20 g, siis elevantide keskmise kaalu hinnang on täpsem (suhtelises mõttes): \(\frac{120}{7000} \approx 0,017 < 0,75 = \frac{1,5}{20}\). Variatsioonikordaja omab mõtet, kui uuritav keskmine ei saa olla 0.

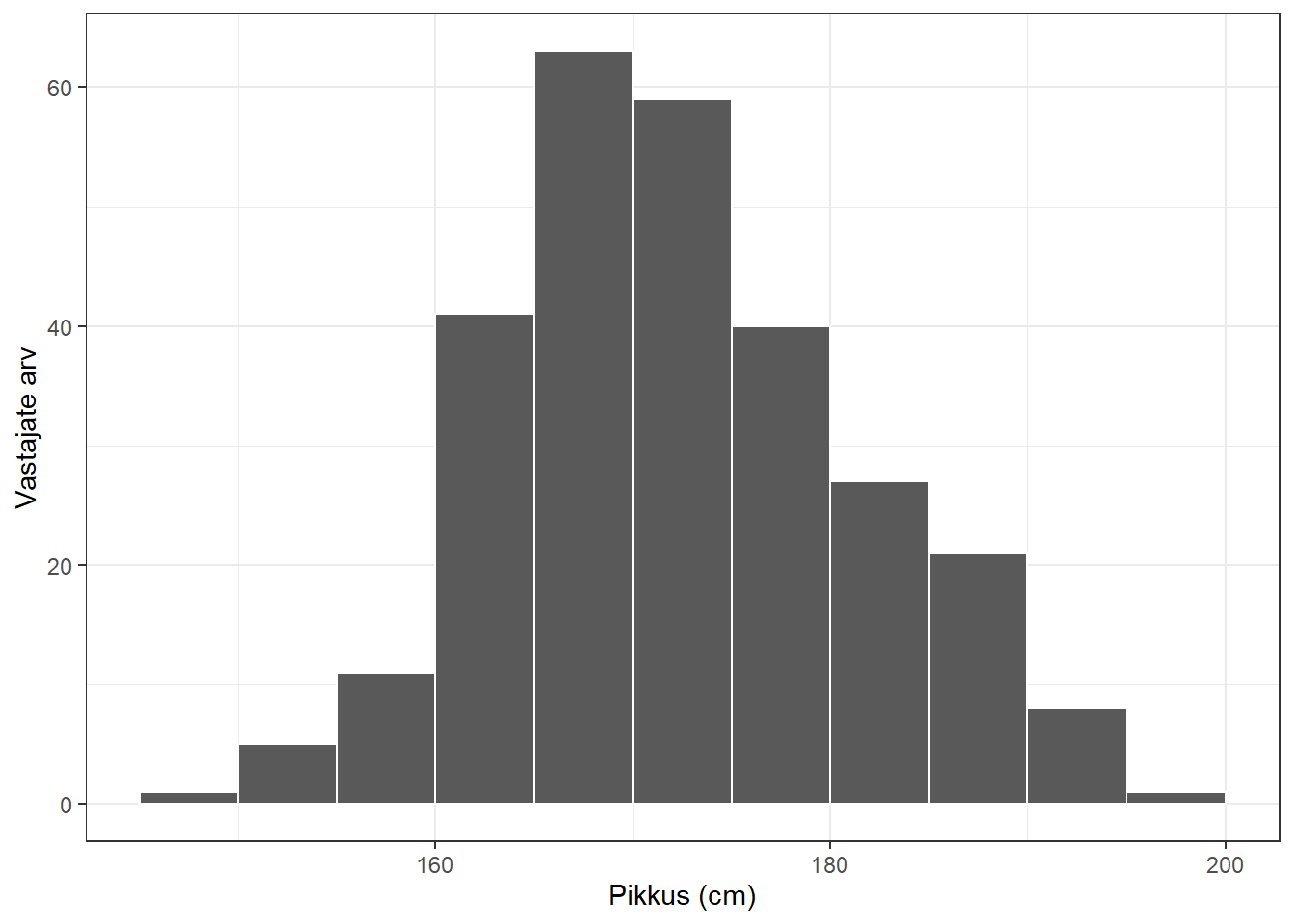
Arvuliste tunnuste jaotuse kirjeldamiseks on mitu sobivat joonist. Üks informatiivsemaid nendest on histogramm. Selle joonistamiseks tuleb pidev tunnus jaotada võrdsete laiustega kategooriatesse ja joonistada tulpadega diagramm, kus y-teljel on vastava kategooria sagedus. Rõhutamaks, et tegemist on arvulise tunnusega, ei jäeta tulpade vahele vahesid ning x-teljele pannakse sildid hoopis tulpade vahele.

Teine sagedane joonis arvuliste tunnuste jaoks on karpdiagramm (boxplot). Karpdiagrammi tuum on karp, mille üks serv kujutab 1. kvartiili ning teine serv 3. kvartiili, karbi keskel olev joon kujutab mediaani (2. kvartiili). Teisisõnu, karbi sisse jääb 50% andmetest, mis paiknevad mediaani ümber. Lisaks sellele lähtuvad karbist nn vurrud, mis iseloomustavad seda, kui kaugele mediaanist jäävad natuke ekstreemsemad väärtused; enamasti ei ole vurru pikkus suurem kui poolteist korda karbi pikkus (võib tarkvarati erineda). Üksikute punktidega kujutatakse selliseid väärtuseid valimis, mis jäävad mediaanist veelgi kaugemale.

Tihti on kasulik arvulise tunnuse jaotust ka jaotustabeli abil iseloomustada. Sel juhul tuleb tunnus kategoriseerida (muuta järjestustunnuseks) ning kasutada sama lähenemist, mida mittearvuliste tunnuste puhul.