5 Statistilised hinnangud

5.1 Jaotuse mõiste

Tavaline kuuetahuline aus täring on selline, millel iga tahu pealejäämise (silmade arv) tõenäosus on sama, 1/6.

Kui teeme katse, kus veeretame täringut 100 korda, siis võib tulemuste jaotus olla hoopis selline:

Tabel 5.1: 100 täringuviske tulemused
	Silmade arv
	1	2	3	4	5	6
Tulemuste arv	19	14	19	12	18	18
Tulemuste osakaal	0.19	0.14	0.19	0.12	0.18	0.18

Katseseerias saadud tulemuste jaotust nimetatakse empiiriliseks jaotuseks, meie poolt eeldatud jaotust, kus kõigil tahkudel on võrdne tõenäosus, aga teoreetiliseks jaotuseks. Üldiselt ongi taoliste katsete läbiviimise mõte hinnata empiirilise jaotuse abil, milline võiks olla antud fenomeni nn päris ehk teoreetiline jaotus. Mida rohkem katseid/mõõtmisi teha, seda rohkem on infot teoreetilise jaotuse kohta ja seda täpsem see loodetavasti on. Näiteks kui visata sama täringuga 100000 viset, võivad tulemused olla sellised:

Tabel 5.2: 100000 täringuviske tulemused
	1	2	3	4	5	6
Tulemuste arv	16698	16652	16801	16595	16761	16493
Tulemuste osakaal	0.167	0.167	0.168	0.166	0.168	0.165

Näiteks kui uurida veregruppide (AB0-süsteemis) levimust, võib alleelide esinemissageduse järgi tuletada geontüüpide tasakaalupunkti (teoreetilise jaotuse), kui populatsioon on Hardy-Weinbergi mõttes tasakaalus¹⁶. Seejärel saab seda võrrelda genotüüpide (0, A, B, AB) tegeliku (empiirilise) jaotusega.

Teoreetiliste jaotuste teadmine kulub niisiis marjaks ära.

Olukord, kus kõigi tulemuste saamise tõenäosus on sama, on tegemist ühtlase jaotusega. Näiteks täringu silmade arv on teoreetiliselt ühtlase jaotusega, samuti mündiviske tulemus. Ka pidevate tunnuste puhul on mõnikord tegemist ühtlase jaotusega, näiteks Geigeri loendajani/andurini jõuavad radioaktiivse aine poolt emiteeritavad osakesed selliste ajavahemike tagant, mis on ühtlase jaotusega¹⁷

5.2 Normaaljaotus ja tema omadused

Teeme katse, kus viskame münti mitu korda (\(N\) korda), ja loendame, mitmel korral selles viskeseerias tuli “kull”. Teeme seda katset (loendame viskeseerias tulnud “kullide” arvu) näiteks 10946 korda. Seega saame justkui 10946 summat, kui summeerimisel loeme, et kiri = 0 ja kull = 1. Näiteks kui viskame 3 korda münti, millest kahel korral tuleb kull, siis selle viskeseeria summa on 2.

Allolevatel joonistel on kujutatud katsete tulemuste histogrammid erinevate viskeseeriate pikkuste \(N\) korral.

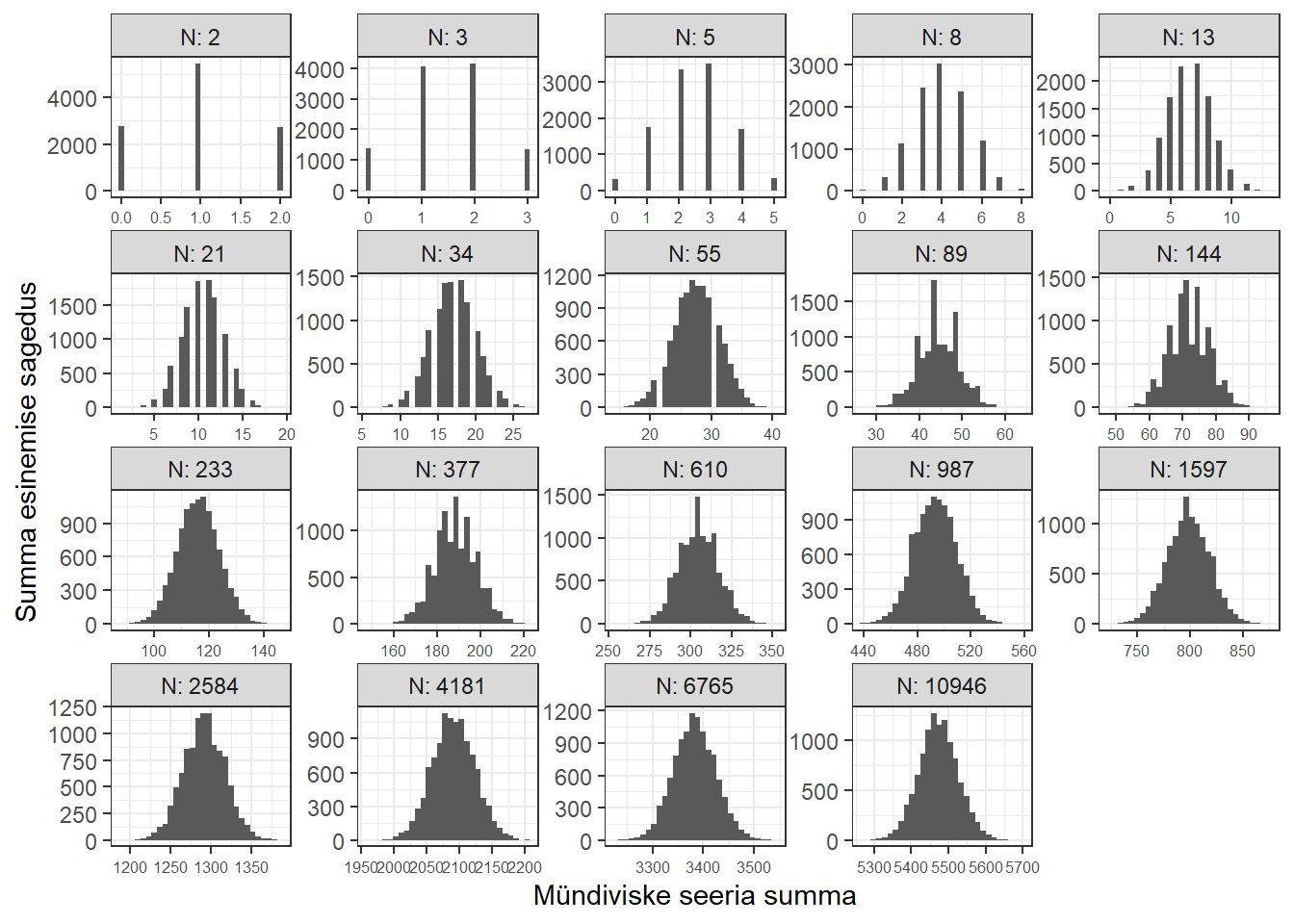
Nagu jooniselt näha, siis mida rohkem me münti viskame, seda nn siledamaks muutub mündiviske tulemuste summade histogramm (igal pildil on kokku 10946 viskeseeriat).

See jaotus, millele mündivisekeseeriate summade jaotus läheneb, on normaaljaotus.

Üksiku mündiviske tulemus (juhuslik suurus, \(x_i\)) on binaarne (kiri või kull). Iga mündivike tulemus on eelmisest sõltumatu, samas kõigil mündivisetel on kulli tulemise tõenoäsus sama. Praegu summeerisime üksikute mündivisete tulemused. Mida pikem oli viskeseeria (ehk mida suurem oli \(N\)), seda sarnasemkas muutus summade histogramm normaaljaotuse histogrammile. See on oluline tähelepanek. Nimelt:

Väide 5.1 Sõltumatute ja sama jaotusega juhuslike suuruste summa \(x_1+x_2+\dots+x_N\) jaotus ligineb normaaljaotusele, kui \(N\to\infty\).

See on mehhanism, kuidas nn looduses normaaljaotus tekib. Seda mehhanismi (sõltumatute sama jaotustega juhuslike suuruste summa jaotus koondub normaaljaotuseks) nimetatakse tsentraalseks piirteoreemiks (central limit theorem) ning see on teoreetilises statistikas üks olulisemaid tulemusi.

Paljud asjad päris-maailmas on mõjutatud üksteisest sõltumatute väga väikse mõjuga tegurite poolt. Näiteks inimese pikkust mõjutavad paljud geenid ning iga üksiku geeni mõju on väike, seepärast ongi pikkuse histogramm sarnane normaaljaotusega.

Vaatame lähemalt, mis see normaaljaotus täpsemalt on. Kui genereerida juhuslikke arve normaaljaotusest, millel teoreetiline keskmine (keskväärtus) on \(\mu\) (statistikažargoonis teoreetilisi arve ehk jaotuse parameetreid tähistatakse sageli kreeka tähtedega, valimi põhjal arvutatud statistikuid aga ladina tähtedega) ning teoreetiline standardhälve on \(\sigma\), siis selliste arvude histogramm on nn kellukesekujuline, nii et kellukese tipp asub x-teljel \(\mu\) kohal.

Samuti on pool histogrammist on keskväärtusest vasakul, pool paremal, järelikult nende arvude mediaan on samuti \(\mu\) – mediaan võrdub keskväärtusega.

Enamgi veel, see histogramm on sümmeetriline, st mistahes \(q\)-kvantiil, kus \(q < 0,5\), on mediaanist sama kaugel, kui tema vastandkvantiil \(1-q\). Näiteks ülal kõige viimasel väiksel histogrammil on 0,33-kvantiil (33. protsentiil) = 5449,99, mis on mediaanist (5473) sama kaugel, kui 0,67-kvantiil (67. protsentiil) = 5496,01. Ja näiteks 0,05-kvantiil (5386,96) on mediaanist sama kaugel kui 0,95-kvantiil (5559,04).

Tänu normaaljaotuse sümmeetrilisusele saab öelda, et vahemikku \(q\)-kvantiil kuni \((1-q)\)-kvantiil jääb mingi % kõigist väärtustest. Normaaljaotuse puhul on juhtumisi nii, et

vahemikku \(\mu\pm\sigma\) jääb umbes 68% kõigist väärtustest (täpsemini u 68,3; 68,0% väärtustest jääb hoopis vahemikku \(\mu\pm 0,974\sigma\)),
vahemikku \(\mu\pm 2\sigma\) jääb umbes 95% kõigist väärtustest (täpsemini u 95,4; 95% väärtustest jääb hoopis vahemikku \(\mu\pm 1,960 \sigma\)),
vahemikku \(\mu\pm 3\sigma\) jääb 99,7% kõigist väärtustest (see on nii).

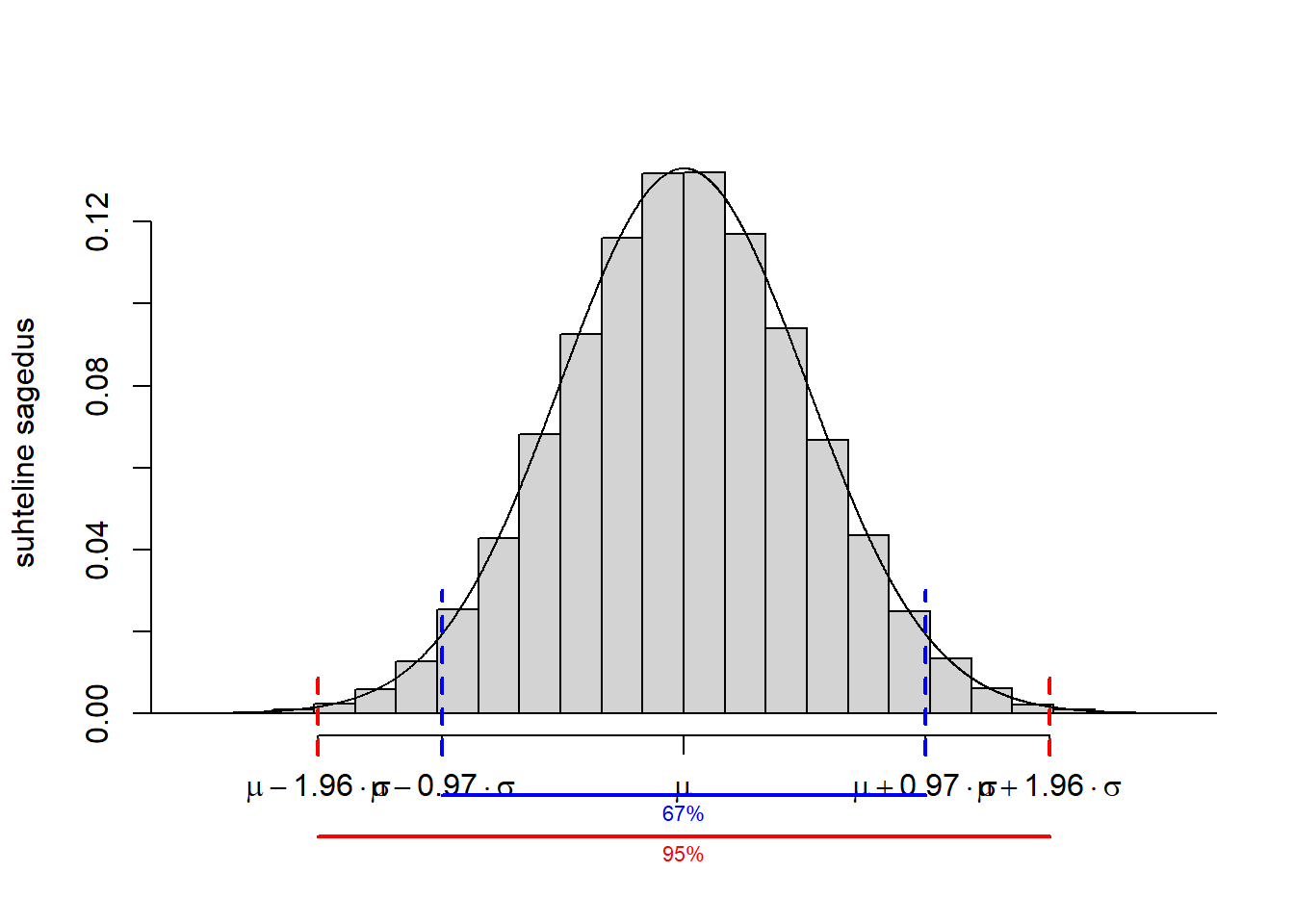
Joonis 5.1: Normaaljaotuse omadused

Normaaljaotuse jaotusfunktsioon

Teoreetilisi jaotuseid kirjeldatakse

tõenäosusfunktsiooniga, kui ei ole tegemist pideva arvulise tunnusega;
jaotusfunktsiooniga, kui on tegemist pideva arvulise tunnusega.

Näiteks mingi konkreetse ebaausa mündi viskamise puhul, kus mõlema külje maandumise tõenäosus on võrdne, saab tulemuse teoreetilist jaotust kirjeldada sellise jaotusfunktsiooniga: \[ P(X=x)=\begin{cases} 0,6 & \text{, kui }x=\text{'kull'}\\ 0,4 & \text{, kui }x=\text{'kiri'} \end{cases} \]

Samamoodi saab sobivate tõenäosusfunktsioonide (mis tegelikult loetlevad üles võimalikud variandid ning nende tõenäosused) abil ära kirjeldada kõigi mittepidevate tunnuste jaotused.

Pidevate arvuliste tunnuste puhul on asjalood natuke teised. Näiteks kui esitada juhuslikult valitud inimese pikkuse \(X\) kohta selline tõenäosuslik küsimus: \[P(X=174\text{ cm})=?,\] siis tuleb silmas pidada seda, et \(174=174,000000000000\dots\; .\)

Teisisõnu: proovige reaalarvude teljele noolt visates tabada lõpmatult täpselt mõnd reaalarvu sel teljel. See on võimatu, sest ühelgi punktil reaalarvude teljel pole suurust (st suurus on null). Samuti pole mitte ühelgi reaalarvude vektorruumi punktil suurust (näiteks kahemõõtmelises ruumis, kus mõlemad teljed (koordinaadid) koosnevad reaalarvudest.

Seepärast ei uurita pidevate arvuliste tunnuste puhul mitte punktide tõenäosuseid, vaid mingite arvuvahemike (intervallide) tõenäosuseid. Ehk siis sõnastatakse küsimus ümber: kui suur on tõenäosus, et inimene on vähemalt 174 cm pikk: \[P(X\leqslant174)=?\] Ehk siis: kui tõenäoline on, et pikkus on 174,000… cm, 173.999… cm (muide, 174,000… on tegelikult täpselt sama arv, mis 173,999…), või et pikkus on 173,999…9899… cm või 173,999…98999…8999… cm jne. Kõik need arvud paiknevad üksteisega lõpmatult tihedalt koos: iga kahe arvu vahel leidub alati veel üks arv.

Sellistes situatsioonides tuleb summa leidmiseks appi tema vend – integraal (muide, mõõduteoorias, mille alla tõenäosusteooria liigitub, kasutatakse tegelikult Lebesque’i, mitte Riemanni’i integraali).

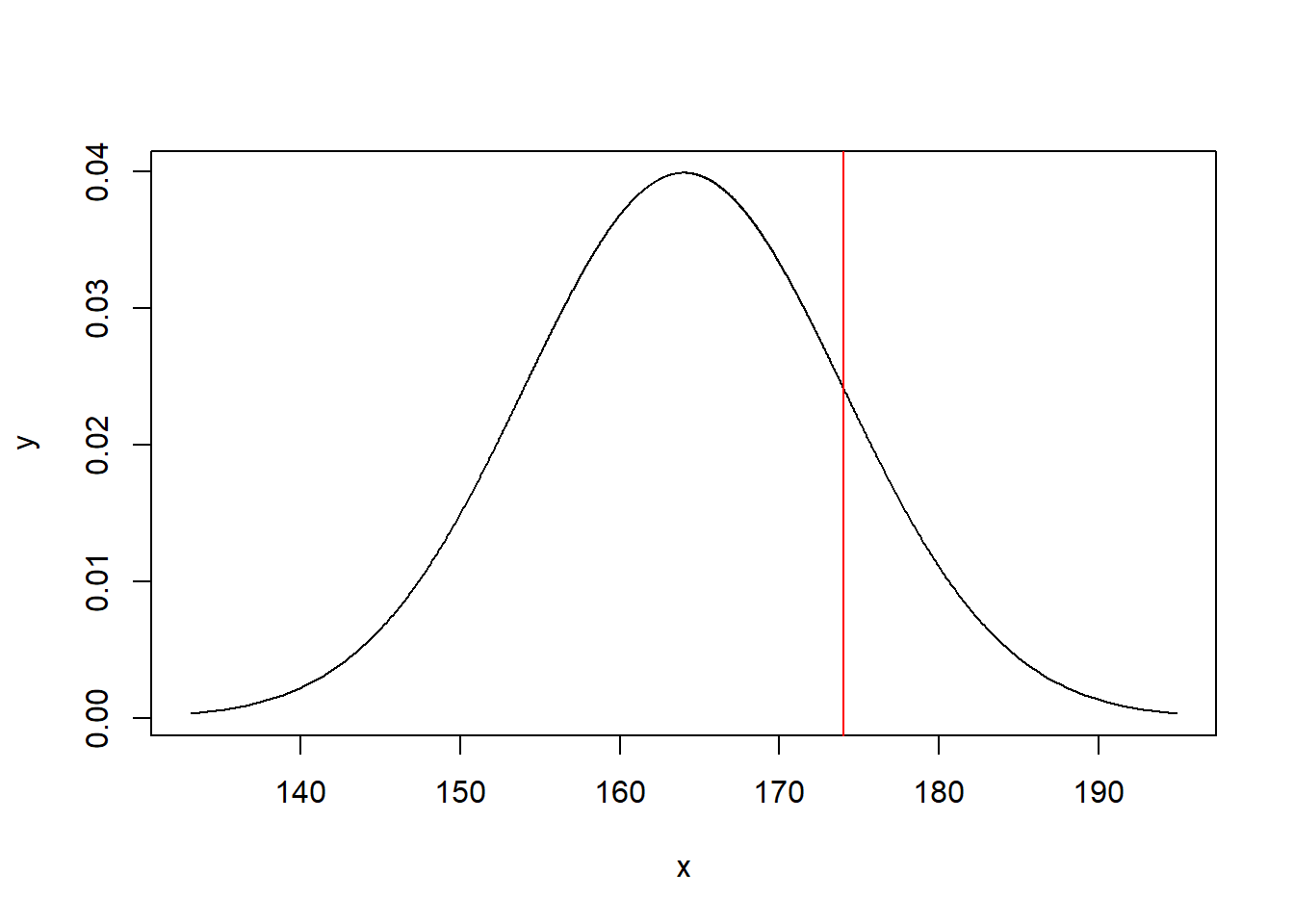
Pidevate tunnuste jaotumist defineerib tihedusfunktsioon (density function), mida enamasti tähistatakse väga originaalselt: \(f(x)\). Jaotusfunktsioon (distribution function), on tihedusfunktsiooni integraal: \[P(X\leqslant x)=\int_{-\infty}^{x}f(t)\text{d}t\]

Normaaljaotuse keskväärtusega \(\mu\) ja standardhälbega \(\sigma\) puhul on tihedusfunktsioon \[f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{\mu - x}{\sigma}\right)^2}\] See ongi see kellukesekujuline kõver, mida enamasti normaaljaotust kujutavatel joonistel näha on.

5.3 Usaldusvahemik

Eelnevalt sai demonstreeritud, kuidas juhuslike arvude (sõltumatud, samast jaotusest) summa järgib normaaljaotust (kui neid arvusid / liidetavaid on piisavalt palju). Tegelikult väidab tsentraalne piirteoreem isegi enamat: nende arvude (juhusliku suuruse realisatsioonide) aritmeetiline keskmine (\(\bar x = \sum_{i=1}^{N}x_i\)) järgib normaaljaotust, millel on sama keskväärtus, kui sellel juhuslikul suurusel.

Võtame näiteks 2001.–2020. a 2. kursuse arstitudengid. Nende kehamassiindeksid on jaotunud selliselt:

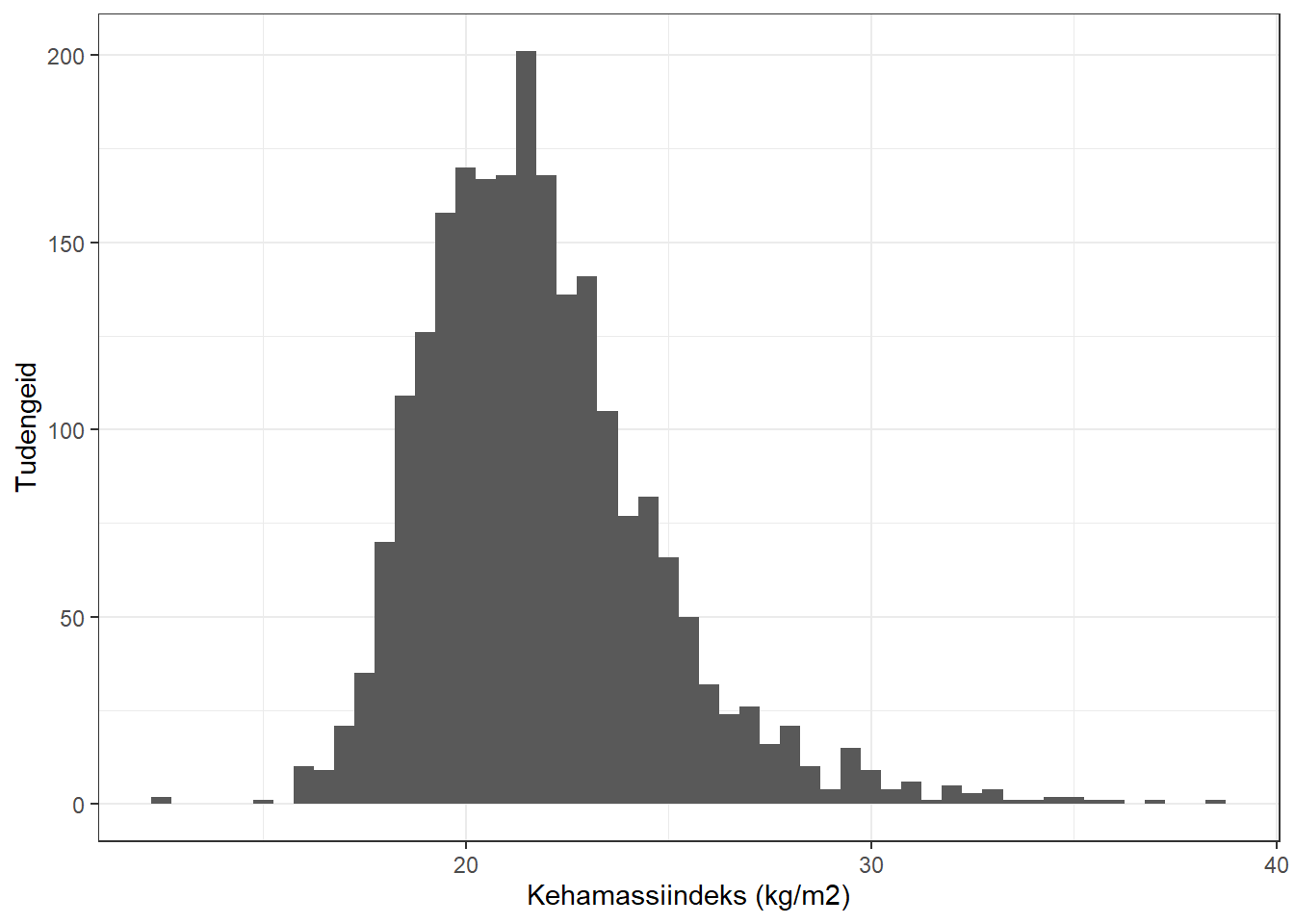
Nagu näha, siis see jaotus on üsna ebasümmeetriline: parempoolne nn saba on palju paksem ja pikem kui vasakpoolne. Keskmine KMI on selles rahvastikurühmas 21,83. Võtame sellest hulgast 200 tudengiga juhuvalimi, sellises valimis tuleb keskmine KMI 22,00. Võtame sellest populatsioonist uuesti juhuvalimi 100 tudengiga, selle valimi keskmine tuleb 21,68. Kordame seda valimi võtmist ja keskmise arvutamist 3000 korda.

Alloleval joonisel on järjestikuste katsete tulemused, punase joonega on kujutatud üldkogumi (2001-2020 arstitudengid teiselt kursuselt) tegelik keskmine KMI. Sellele järgneval joonisel on kujutatud katsetulemuste jaotus.

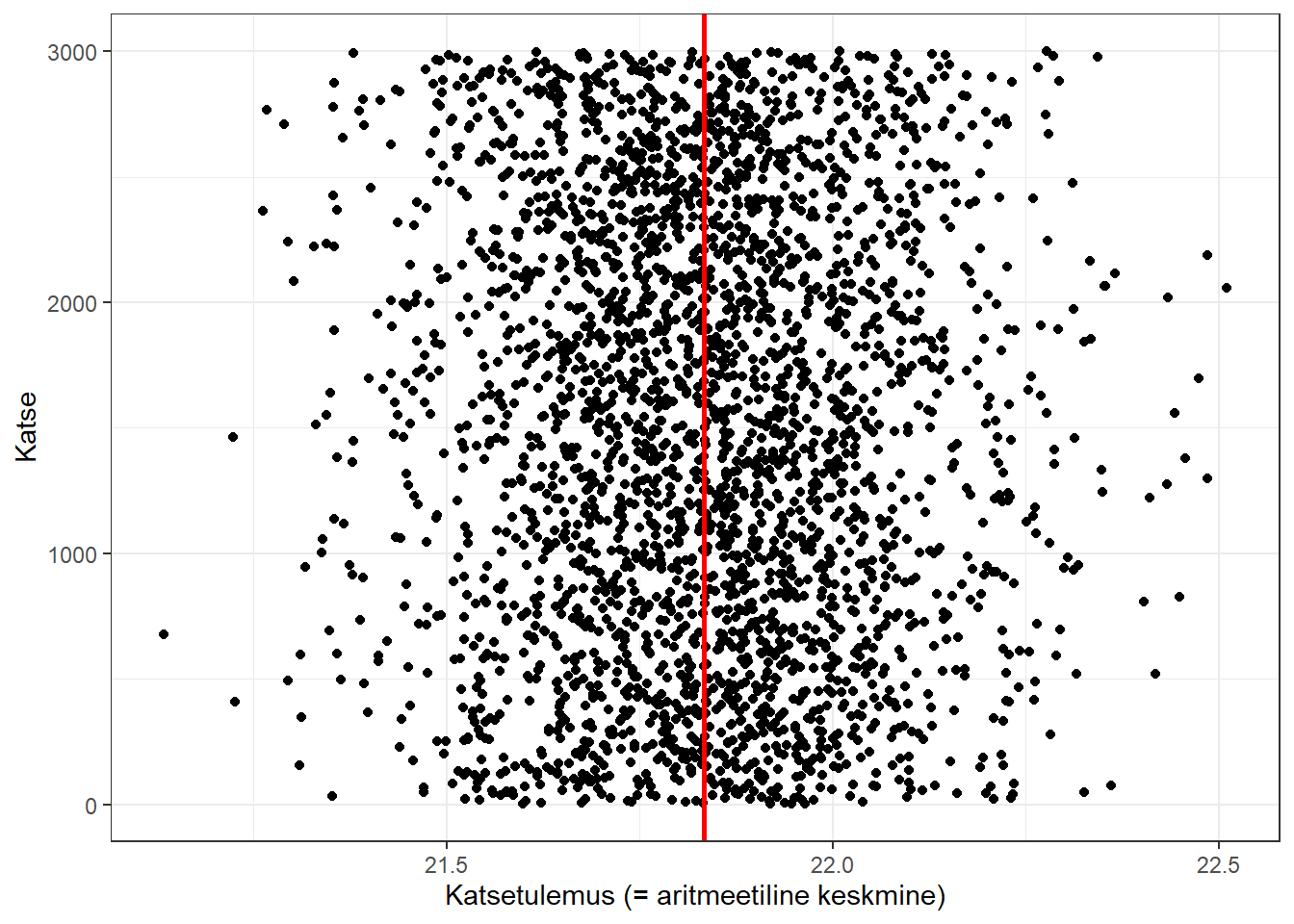
Joonis 5.2: Juhuvalimist saadud aritmeetilised keskmised katsete kaupa

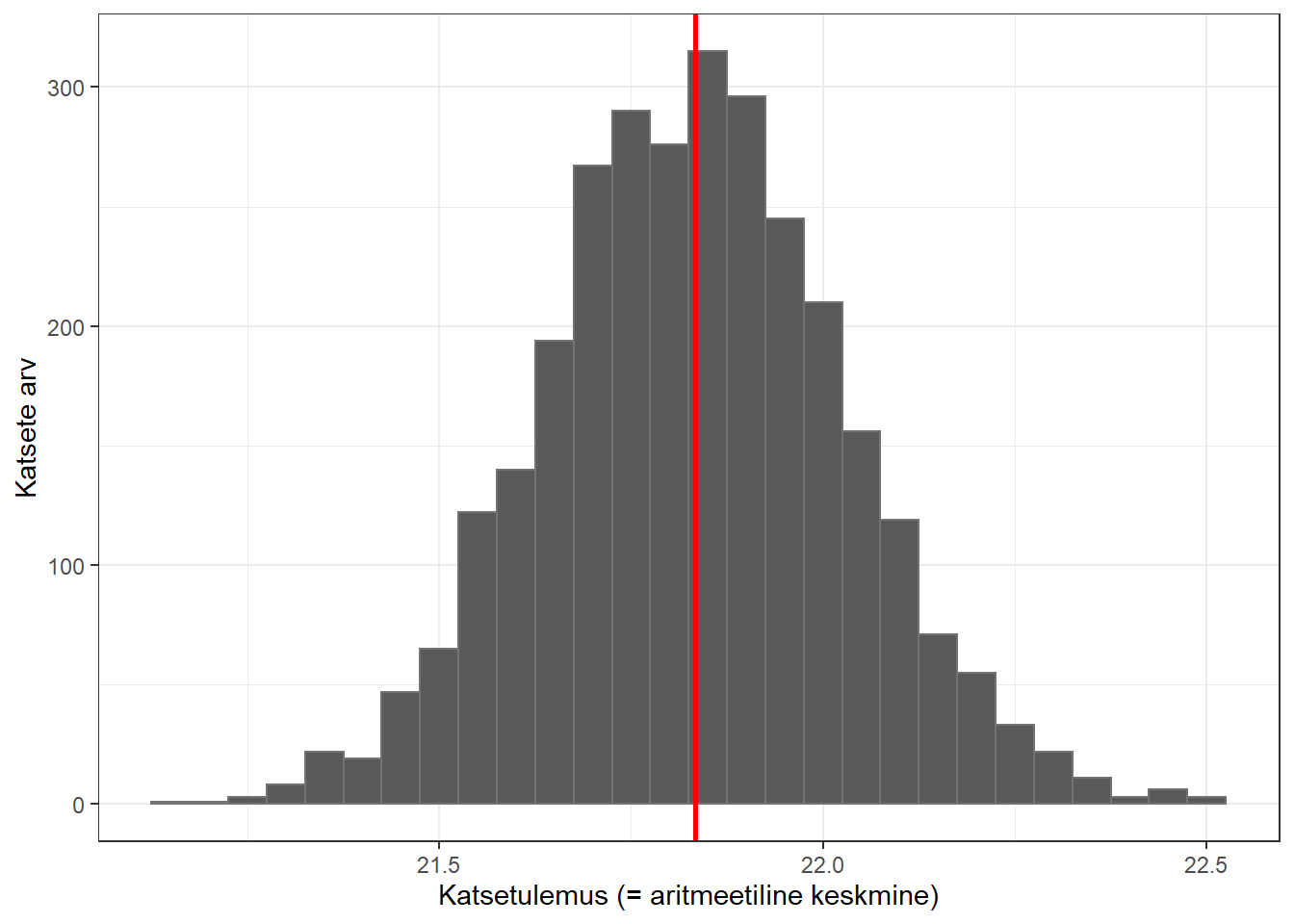
Joonis 5.3: Katsetulemuste jaotus

Nagu näha, siis valdav osa katsetulemusi tuli tegeliku keskmise KMI lähedale; teatav osa tuli keskmisest natuke kaugemale ning üsna väike osa hälbis tegelikust keskmisest KMIst märgatavalt. Neis 3000 katses arvutatud katsetulemuste (aritmeetiliste keskmiste) põhjal arvutatud aritmeetiline keskmine on 21,83, standardhälve on 0,20. Seda – lõpmatult paljude katsete tulemuste – standardhälvet nimetatakse standardveaks.

Definitsioon 5.1 Standardviga (standard error, SE) on hinnatava statistiku teoreetiline standardhälve.

Hinnatav statistik on meil praegu KMI keskväärtus (st üldkogumi tegelik aritmeetiline keskmine KMI); kuna me tegime hästi palju katseid, siis seetõttu nende katsete põhjal hinnatud standardviga (kõigi katsetulemuste põhjal arvutatud standardhälve) on üsna lähedal tegelikule ehk teoreetilisele standardveale.

Kõigist 3000 katsetulemusest oli 69,3% keskmisest katsetulemusest mitte kaugemal kui 1 standardviga, 95,3% aga mitte kaugemal kui 2 standardviga.

Järelikult: piisavalt suure valimiga tehtud katsete tulemused järgivad normaaljaotust, mille keskväärtus on üldkogumi tegelik keskväärtus.

Teisisõnu, kui me teeme ühe uuringu (ehk katse; nt ühe valikuuringu või siis ühe kliinilise katse), siis me teame seda, et uuringuga saadud tulemus tõenäoliselt on tegelikule huvipakkuvale parameetrile (nt üldkogumi keskmisele) üsna lähedal. Sealjuures u 95%-lise tõenäosusega ei ole selles uuringus saadud tulemus nn õigest väärtusest kaugemal kui 2 x standardviga.

AGA: kui me teeme ühe ühe uuringu, siis on meil ju vaid üks uuringutulemus, mitte näiteks 3000 erineva uuringu tulemust, mille põhjal standardviga (uuringutulemuste standardhälvet) arvutada. Õnneks on tõenäosusteooriast teada, et üksikute mõõtmistulemuste standardhälbe ning mõõtmistulemuste arvu (valimi suuruse) ruutjuure suhe on hea hinnang standardveale: \[SE = \frac{s}{\sqrt{n}}\] Väga tore! Seega ei pea tegema mitut uuringut, et teada saada, kui kaugel ühe uuringu tulemus võib nn õigest väärtusest olla. 95%-lise tõenäosusega uuringust saadud aritmeetiline keskmine \(\bar{x}\) ei ole tegelikust üldkogumi keskmisest (\(\mu\)) kaugemal kui \(2 \times \frac{s}{\sqrt{n}}\) (tegelikult \(1,96\times\frac{s}{\sqrt{n}}\)).

Teisisõnu: võime 95% kindlad olla, et vahemik \[\bar{x} \pm 1,96 \times \frac{s}{\sqrt{n}}\] sisaldab üldkogumi tegelikku keskmist \(\mu\). Seda vahemikku nimetatakse 95-protsendiliseks usaldusvahemikuks keskväärtusele.

Definitsioon 5.2 95%-line usaldusvahemik on arvuvahemik, mis hinnatavat üldkogumi parameetrit sisaldab 95%-lise tõenäosusega.

\(p\)%-line usaldusvahemik (confidence interval, CI) on vahemik, mis hinnatavat üldkogumi parameetrit sisaldab \(p\)%-lise tõenäosusega.

Usaldusvahemiku piire kutsutakse alumiseks ja ülemiseks usalduspiiriks (lower/upper confidence limit).

Võimalusi, kuidas rehkendada taolist arvuvahemikku, mis etteantud tõenäosusega meile huvipakkuvat üldkogumi parameetrit sisaldaks, on mitmeid. Eelpool tutvustatud varianti
\[parameeter \pm 1,96 \times SE\] nimetatakse Waldi-tüüpi (95%liseks) usaldusvahemikuks; seda saab kasutada vaid olukorras, kus huvipakkuva parameetri hinnang allub normaaljaotusele. Keskväärtuse hinnang – aritmeetiline keskmine – seda õnneks teeb.

Ega üksiku uuringu puhul me ju tegelikult ei tea, kas 95%-line usaldusvahemik ka päriselt õiget keskväärtust sisaldab. Nende 3000 katse puhul, kus valiti kõigi 2001–2020 arstitudengite hulgast igas katses 200 inimest, juhtus 141 korral nii, et 95%line usaldusvahemik ei katnud tegelikku keskväärtust ära.

Alloleval joonisel on kujutatud katsete nr 668 kuni 687 tulemusi (keskväärtuse hinnang (aritmeetiline keskmine) koos 95%lise usaldusvahemikuga).

Joonis 5.4: Mõnes katses saadud keskväärtuse hinnangud koos 95% usaldusvahemikuga

Katses nr 678 on saadud tulemus, mis on õigest üldkogumi keskväärtusest (punane) üsna kaugel, sealjuures ka usalduspiirid jäävad õigest väärtusest üsna kaugele. Tasub tähele panna, et selles katses on usaldusvahemik märksa kitsam (ÜUP - AUP = 0,69), kui paljud teised sel joonisel olevad usaldusvahemikud. Järelikult: kui usaldusvahemik on üsna kitsas, siis ei pruugi see tähendada, et hinnang on tõesele väärtusele lähedal.

Kuidas soodustada seda, et uuringus saadud hinnang oleks tõele lähedal? Kõige olulisem – valida õige uuringukavand ning uuring korralikult planeerida. Järgmine samm: võtta üldkogumist võimalikult suur valim. Mida suurem on valim, seda suurem on tõenäosus, et uuringu tulemus on tõele lähedal.

Alloleval joonisel on kujutatud tudengite KMI hinnang koos 95%lise usaldusvahemikuga erinevate valimisuuruste korral. Tõepoolest, keskväärtuse hinnang (punkt usaldusvahemiku keskel) on seda lähemal õigele keskväärtusele, mida suurem on valim.

Tasub tähele panna, et kõige suurem valim, kuhu oli kaasatud kogu üldkogum (kõikne valim) – selle valimi puhul on usaldusvahemiku laius 0. Tõepoolest, kui on tegemist kõikse valimiga (kus puuduvaid väärtuseid pole), siis pole vajadust mingisuguseks peeneks arvutuseks usaldusvahemike saamiseks, sest üldkogumi parameetrid on täpselt teada.

Joonis 5.5: Erineva suurusega valimist saadud 95% usaldusvahemikud keskväärtusele

Kui valimisse kaasatakse oluline osa lõplikust üldkogumist (nt valikuuring kaasab 10% või suurema osa rahvastikust), siis on vaja arvesse võtta seda asjaolu, et üldkogum pole lõpmatult suur. Kuidas?

Tegemist on eelkõige valikuuringute teooriat puudutava küsimusega. Kui tegemist on lihtsa juhuvalikuga ilma tagasipanekuta (st et üht inimest kaasatakse valimisse vaid ühe korra), siis keskväärtuse hinnangu puhul on seda üsna lihtne teha: usaldusvahemiku laius ei ole mitte standardvea-kordne, vaid standardviga tuleb koefitsiendiga \[\sqrt{\frac{N-n}{n-1}}\] läbi korrutada (siin \(N\) on üldkogumi suurus ning \(n\) on valimi suurus). Näiteks kui tudengeid on üldkogumis kokku 2262 ning valimi suurus on 1484 ja selles valimis saadi keskmine KMI 21,82 standardhälbega 2,10, siis 95% usaldusvahemik on \[\bar{x} \pm 1,96 \times \frac{s}{\sqrt{n}} \times \sqrt{\frac{N-n}{n-1}}\\= 21,82 \pm 1,96 \times \frac{ 2,10 } {\sqrt{ 1484 }} \times \sqrt{\frac{ 2262 - 1484 }{ 1484 -1}}\]

ehk 21,7 kuni .

Kui vaadata keskväärtuse hinnangu standardvea hinnangut (\(SE = \frac{s}{\sqrt{n}}\)), siis on selge, et lisaks valimi suurusele \(n\) mõjutab usaldusvahemiku laiust ka valimis nähtav standardhälve \(s\): mida varieeruvamad on valimis mõõtmistulemused, seda suurem on nende põhjal hinnatud keskväärtuse standardviga. Ent nagu ülalt jooniselt 5.4 oli näha (seal olid kõik valimid sama suured, seega 95% usaldusvahemiku laiuse määras vaid standardhälve) ei pruugi väiksem standardhälve tähendada seda, et uuringus saadud hinnang on üldkogumi parameetrile lähedal.

Kui vaadata Waldi usaldusvahemiku arvutamise valemit \[hinnang \pm kordaja \times SE,\]

siis on selge, et lisaks standardveale (mida mõjutavad valimi suurus ja mõõtmistulemuste standardhälve) mõjutab usaldusvahemiku laiust ka see kordaja, millega standardviga läbi korrutatakse. Kust see kordaja tuleb?

Nagu teada, siis normaaljaotuse puhul 95% kõigist väärtustest jääb vahemikku \(keskväärtus \pm 1,96 \times standardhälve\) (kui meie mõõtmistulemuseks on üldkogumi mingi parameeter, siis standardhälvet nimetatakse standardveaks) ning 90% kõigist väärtustest jääb vahemikku \(keskväärtus \pm 1,64 \times standardhälve\).

Näiteks sellisel normaaljaotusel, millel keskväärtus \(\mu = 0\) ning standardhälve \(\sigma = 1\), jääb 90% kõigist väärtustest vahemikku -1,64…1,64. Sellist normaaljaotust, mille keskväärtus on 0 ning standardhälve on 1, nimetatakse standardnormaaljaotuseks (standard normal distribution).

Kuna standardnormaaljaotuse keskväärtus on 0 ja standardhälve 1, siis järelikult vahemikku \(0 \pm 1,96 \times 1\) ehk \(-1,96 \ldots +,96\) jääb sellel jaotusel 95% kõigist väärtustest. Järelikult need arvud, \(-1,96\) ja \(+1,96\) on standardnormaaljaotuse 0,025- ning 0,975-kvantiilid (ehk 2,5. ja 95,5. protsentiil). Niisiis on hea, kui Waldi-tüüpi usaldusvahemiku arvutamisel on käepäerast tabel standardnormaaljaotuse kvantiilidega. Kuna standardnormaaljaotus – nagu iga muugi normaaljaotus – on sümmeetriline, siis tema kvantiilid asuvad mediaanist (0) võrdsel kaugusel. Seega piisab vaid sellest, kui teame pooli kvantiile (nt mediaanist suuremaid kvantiile); ülejäänud pool on samad, aga vastupidise märgiga.

Tabel 5.3: Standardnormaaljaotuse mõned kvantiilid
p%-line UV	Mitmes kvantiil?	Kvantiili väärtus (SE kordaja)
20	0,600	0,2533
40	0,700	0,5244
60	0,800	0,8416
70	0,850	1,0364
80	0,900	1,2816
90	0,950	1,6449
95	0,975	1,9600
98	0,990	2,3263
99	0,995	2,5758

Joonis 5.6: Standardnormaaljaotuse kvantiilid (tihedusfunktsioon)

Joonis 5.7: Standardnormaaljaotuse kvantiilid (jaotusfunktsioon)

Kuna see omadus, et vahemik \(\mu \pm z_q \times \sigma\) (kus \(z_q\) on q-nda kvantiili väärtus, \(q<0,5\)) sisaldab \(1-2q\) osa kõigist normaaljaotuse väärtustest – see omadus kehtib kõigi normaaljaotuste puhul, siis piisab sellest, kui teame standardnormaaljaotuse kvantiile. Kasutades neid standardhälbe kordajatena, teame seeläbi kõigi normaaljaotuste kvantiile.

5.4 t-jaotus

Standardnormaaljaotuse kvantiile (nt 0,975-kvantiil on 1,96) saab keskväärtuse hinnangu usaldusvahemiku arvutamiseks kasutada, kui valim on piisavalt suur (hea oleks, kui > 100, veel parem, kui > 200 objekti). Nimelt, keskväärtuse hinnangu standardviga \(\frac{s}{\sqrt{n}}\) sisaldab valimi juhuslikkusest tulenevat viga – nimetajas olev mõõtmistulemuste standardhälve \(s\) on seepärast natuke ebatäpne hinnang tegelikule standardhälbele \(\sigma\). Mida väiksem valim, seda ebatäpsem. Sel põhjusel tuleks kasutada väikse valimi puhul hoopis t-jaotuse kvantiile, mille väärtus sõltub otseselt valimi suurusest. Nimelt on t-jaotus peaaegu samasugune kui standardnormaaljaotus, ent mida väiksem on nn vabadusastmete arv (degrees of freedom, lihtsamas olukorras \(df = \text{valimi suurus} - 1\)), seda nn lapikum see jaotus on.

Tabel 5.4: t-jaotuse kvantiilid erineva \(n\) korral
	Mitmes kvantiil:
n	0.8	0.9	0.95	0.975	0.99	0.995	0.999
5	0.94	1.53	2.13	2.78	3.75	4.60	7.17
10	0.88	1.38	1.83	2.26	2.82	3.25	4.30
20	0.86	1.33	1.73	2.09	2.54	2.86	3.58
30	0.85	1.31	1.70	2.05	2.46	2.76	3.40
50	0.85	1.30	1.68	2.01	2.40	2.68	3.27
75	0.85	1.29	1.67	1.99	2.38	2.64	3.20
100	0.85	1.29	1.66	1.98	2.36	2.63	3.17
200	0.84	1.29	1.65	1.97	2.35	2.60	3.13

Alloleval joonisel on nelja erineva jaotuse kvantiilid:

N(0, 1) – normaaljaotus keskväärtusega 0, standardhälbega 1 (ehk standardnormaaljaotus)
t(df=4) – t-jaotus vabadusastmete arvuga 4 (ehk vastav valimi suurus on 5)
t(df=29) – t-jaotus vabadusastmete arvuga 29 (ehk vastav valimi suurus on 30)
t(df=99) – t-jaotus vabadusastmete arvuga 99 (ehk vastav valimi suurus on 100)

Joonis 5.8: Mõningate t-jaotuste ning standardnormaaljaotuse tihedusfunktsioonid koos kvantiilidega

5.5 Mõnede statistikute ning seosenäitajate usaldusvahemikud

5.5.1 Protsendi hinnang

Kuna protsendi/osakaalu hinnang on tegelikult nullide ja ühtede aritmeetiline keskmine, siis tsentraalne piirteoreem kehtib ka selle korral: piisavalt suure valimi korral allub protsendi hinnang normaaljaotusele.

Alloleval joonisel on illustratiivne argument, mis seda väidet iseloomustab. Eelpool mainitud arstiteaduse 2. kursuse tudengite hulgast (kus igapäevasuitsetajaid oli 5,8%) valiti juhuslikult 200 tudengit ning arvutati igapäevasuitsetajate osakaal. Seda tehti 10000 korda. Saadud protsendihinnangud jaotusid järgnevalt:

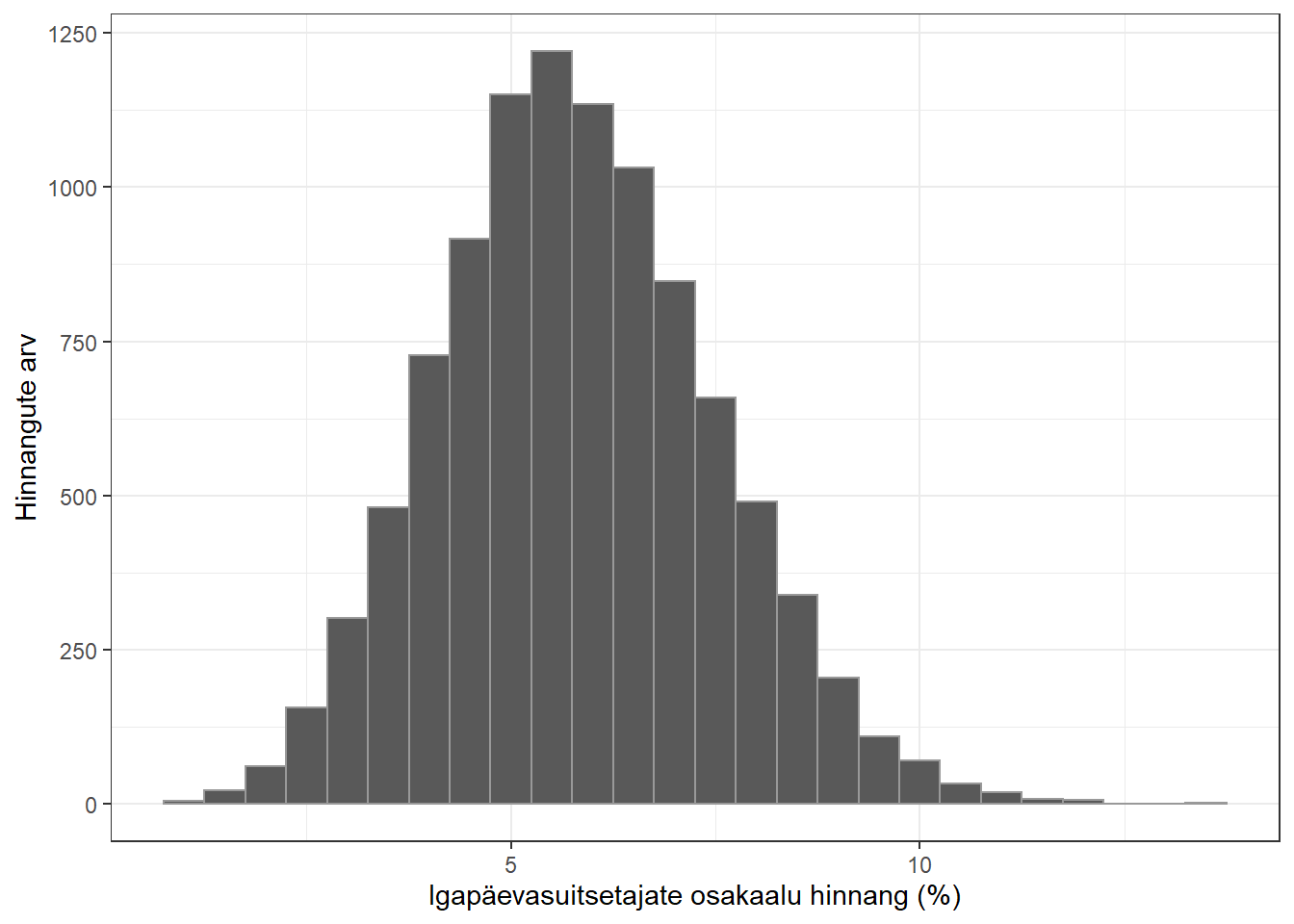
Joonis 5.9: 10 000 simulatsioonis saadud igapäevasuitsetajate osakaalu hinnangute jaotus

Protsendi hinnangu \(p\) standardviga avaldub kujul \(\sqrt{p(1-p)/n}\), seega näiteks 95%-list usaldusvahemikku saab arvutada (kui valim on piisavalt suur, nt > 30 objekti) niiviisi: \[p\pm\sqrt{\frac{p(1-p)}{n}}\]

5.5.2 Riskide vahe

Riskide vahe (absolute risk reduction, ARR) on õnneks lihtne juhtum. Kuna mõlema riski hinnangud (\(p_1\) ja \(p_2\)) alluvad normaaljaotusele ning kuna tõenäosusteooriast on teada, et sõltumatute juhuslike suuruste liitmisel (sh lahutamisel) dispersioonid liituvad, siis riskide vahe 95%list usaldusvahemikku saab arvutada nii (kui mõlemas grupis on piisavalt objekte, nt > 30): \[p_1-p_2 \pm 1,96 \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}\]

5.5.3 Riskide suhe

Jagamine on teadupärast märksa keerukam kui lahutamine. Appi saab võtta matemaatikast tuttava nõksu – logaritmimise. Seeläbi muutub jagamistehe liitmistehteks (st lahutamistehteks). Ja seejärel saab jälle kasutada tõenäosusteooriast tuntud teadmist, et sõltumatute juhuslike suuruste dispersioonid liituvad: 95%-line usaldusvahemik riskide suhtele avaldub järgmiselt: \[\exp{\left(\ln(p_1)-\ln(p_2) \pm 1,96\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}\right)}\]

5.5.4 Šansside suhe

Ka šansside suhte puhul mängib normaaljaotus rolli, aga kuna siin on tegemist väga mitme jagamistehtega, siis detailidesse ei lasku. Õnneks on šansside suhte ligikaudne 95% usaldusvahemik lihtsasti avaldatav, kui kasutada 2x2 tabeli abil: \[\exp\left(\ln(OR)\pm1,96\sqrt{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}}\right),\] kus \(a\), \(b\), \(c\) ja \(d\) on 2x2 sagedustabeli lahtrites olevad sagedused.