7 Korrelatsioon

Eelnevalt oleme tutvunud erinevate statistiliste testidega, mis aitavad võrrelda keskmiseid (või üldisemalt paiknemist) või osakaalusid kahe või enama rühma vahel. Seega üks tunnustest on alati olnud mittearvuline.

Kui on aga tegemist kahe arvulise, eriti kahe pideva tunnusega, on sobiv kasutada korrelatsioonikordajat. Kuna korrelatsioonikordaja on midagi enamat kui statistilise testi p-väärtus, ongi sellele eraldi peatükk pühendatud.

Alloleval joonisel on kujutatud tudengite pikkused ja kaalud. Seos on üsna selge: (keskmiselt) mida pikem on inimene, seda pikem on tema kaal. Kui mõtteliselt jaotada joonis neljaks kvadrandiks (nt horisontaalselt poolitada keskmise kaalu koha pealt ning vertikaalselt keskmise pikkuse kohalt), siis suurem osa punktidest jäävad ülemisse paremasse osasse või alumisse vasakusse osasse.

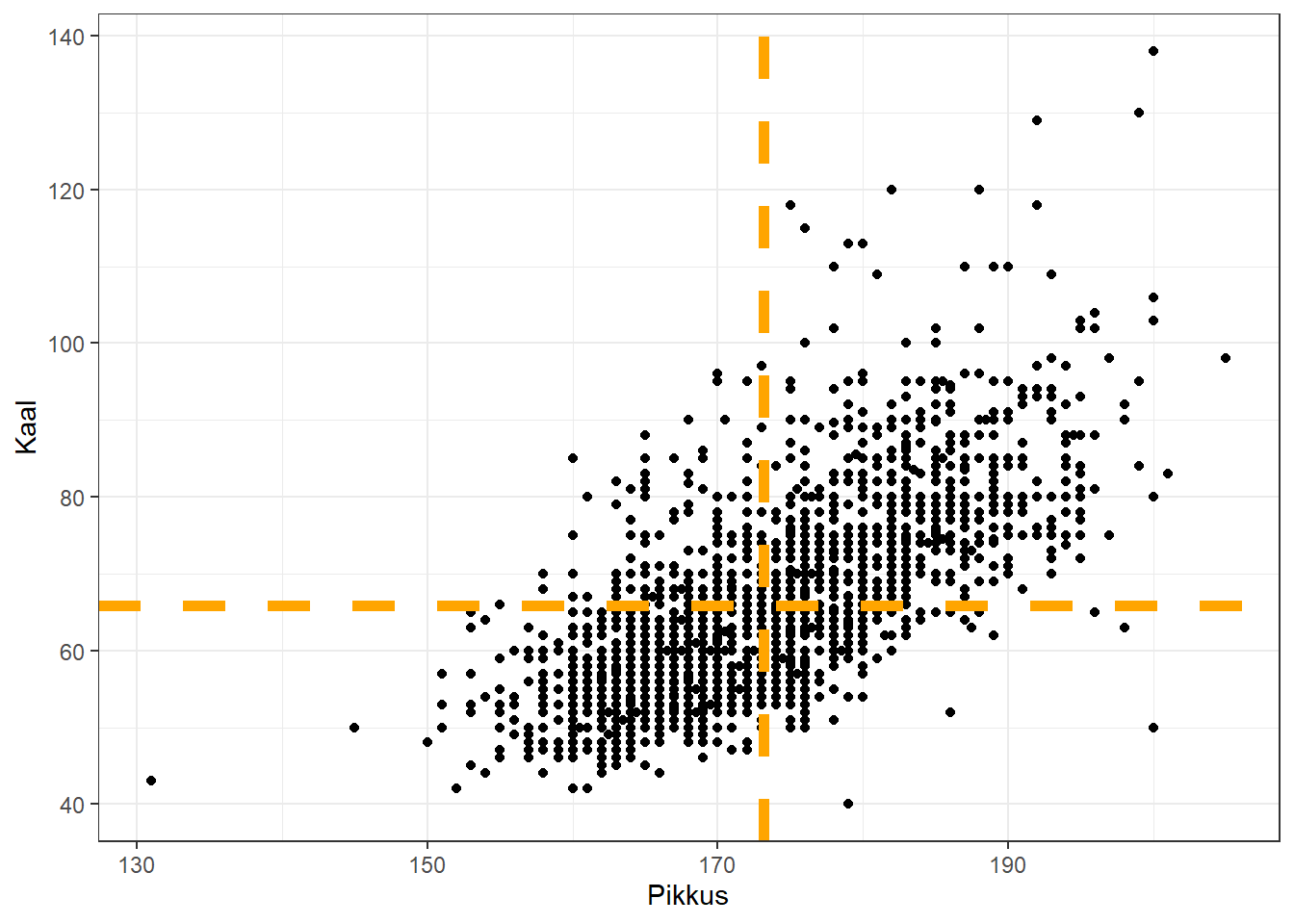
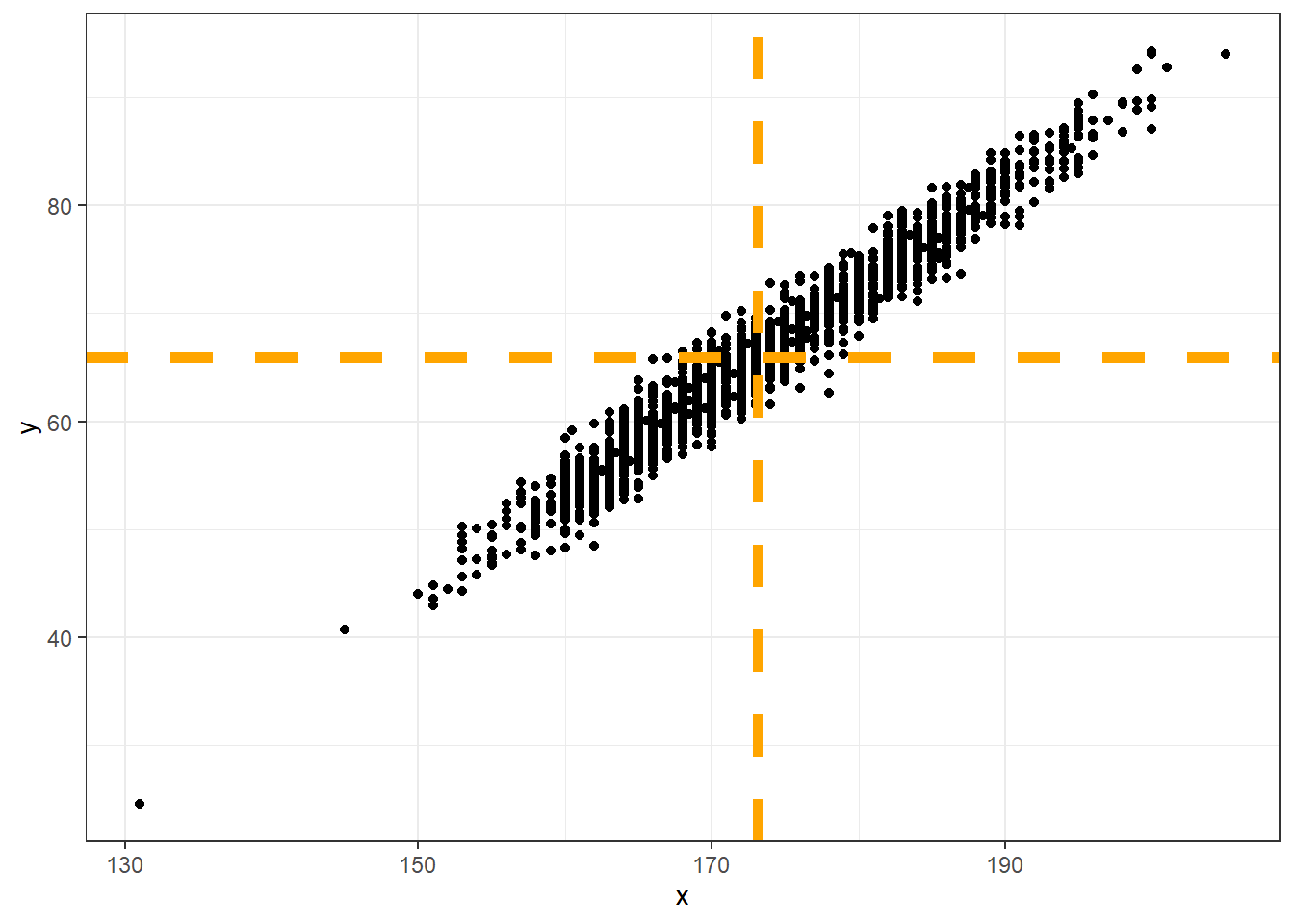
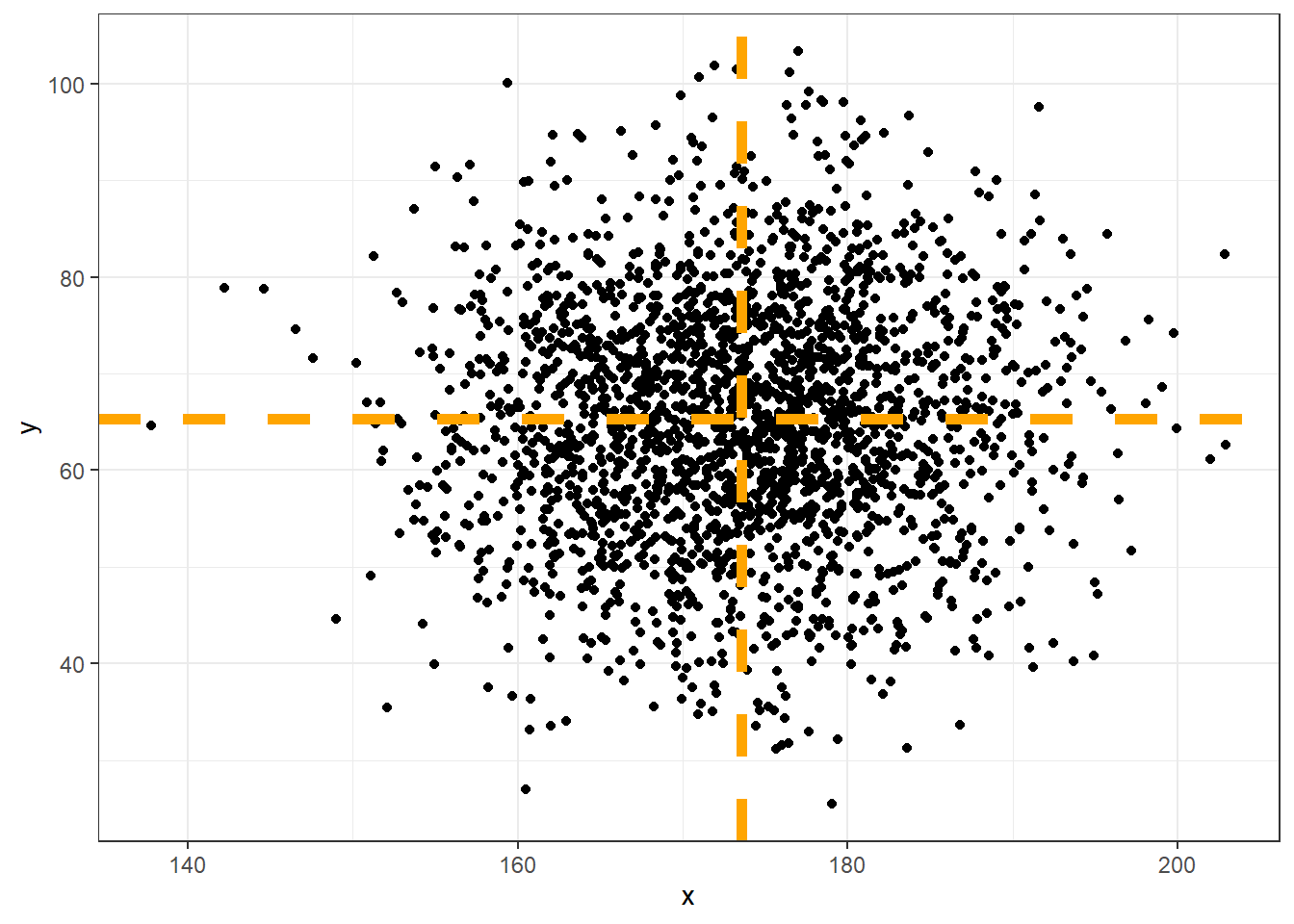
Kui seos pikkuse ja kaalu vahel oleks veelgi tugevam, paikneks rohkem punkte joonise keskosast (pikkuse ja kaalu keskmistest) veelgi kaugemal (alumine vasakpoolne joonis). Kui aga pikkus ja kaal omavahel seotud pole, võiks näha sellist pilti, nagu alumisel parempoolsel joonisel. Sel pildidl oleks igas kvadrandis enam-vähem sama palju punkte ning suurem osa neist on ühele või teisele keskmisele (st keskmisele pikkusele või keskmisele kaalule või mõlemale) mõnevõrra lähemal.

Niisiis võiks võrrelda iga punkti puhul, kui kaugel ta üheagselt asub nii x-tunnuse kui ka y-tunnuse keskmisest. Lisaks võiks vaadata, kas punktid asuvad rohkem esimeses (ülemises parempoolses) ja kolmandas (alumises vasakpoolses) kvadrandis või pigem teises ja neljandas. Seda lähenemist kasutataksegi korrelatsioonikordaja arvutamiseks.

Üksiku punkti (number \(i\)) kaugust üheaegselt nii x-tunnuse kui ka y-tunnuse keskmisest saab väljendada ristküliku pindalaga (mis omab + või - märki): \((x_i - \bar{x})\cdot(y_i - \bar{y})\). Kui punkt asub esimeses või kolmandas kvadrandis, on korrutis +märgiga, kui teises või neljandas kvadrandis, siis -märgiga. Kui ristkülikute pindalad koos märkidega summeerida, siis olukorras, kus esineb nn positiivne ehk võrdeline seos, on +märgiga ristkülikud ülekaalus ning summa tuleb positiivne; mida väljavenitatum see punktipilv on, seda suuremad tulevad ka ristkülikute pindalad ning seda suurem tuleb ka summa \[\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})\;.\] Loomulikult sõltub summa suurus punktide arvust ehk valimi suurusest. Et teha see summa tõlgendatavaks erinevate valimite puhul, saab seda valimi suurusega läbi jagada. Kui veel lisaks läbi jagada teguriga \(s_x \cdot s_y\) (x ja y tunnuse standardhälvete korrutis), on tulemuseks arv, mis alati jääb -1 ja +1 vahele. Seda arvu nimetatakse Pearsoni korrelatsioonikordajaks (sageli tähistatakse \(\rho\) või \(r\)): \[r = \frac{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{s_x^2 \cdot s_y^2}\] Tihti, kui jutuks on “korrelatsioonikordaja” ja mingit täiendavat täpsustust ei ole, on silmas peetud justnimelt Pearsoni korrelatsioonikordajat.

Alloleval vasakpoolsel joonisel on näitlikustamiseks 5 inimese pikkused ja kaalud; nende põhjal arvutatud Pearsoni korrelatsioonikordaja väärtus tuleb 0,66. Nagu näha, siis valdavalt on pikkused umbes 160 cm kandis, ent ühel isikul on pikkus üle 180 cm. Kuna see asub keskmisest pikkusest (165,2 cm) võrdlemisi kaugel, siis sellele ühele isikule vastava ristküliku pindala on ka üpris suur. Seetõttu on selle ühe isiku osakaal korrelatsioonikordaja väärtuses samuti üpris suur.

Andmepunkti, mis asub ülejäänud vaatlustest ebaharilikult kaugel, nimetatakse erindiks.

Kuidas vähendada taoliste erindite liigset mõju/osakaalu? Lihtne, juba tuntud võte: kasutame päris mõõtmistulemuste asemel järjekorranumbreid (astakuid), korrelatsioonikordaja arvutusvalemi aga jätame samaks. Taolisel viisil arvutatud korrelatsioonikordajat nimetatakse Spearmani (astak-)korrelatsioonikordajaks (mõnikord tähistatakse \(r_{\tiny{Spearman}}\)). Ülemisel parempoolsel joonisel on näha, kuidas sel moel tegutsedes ristkülikud moodustuvad. Nagu näha, on punktide osakaalud (ristkülikute pindalad) nüüd üksteisele märksa sarnasemad.

7.1 Korrelatsioonikordaja tõlgendamine

On lihtne ette kujutada punktipilvi, kus x ja y tunnuse vahel imselgelelt on seos, aga kus igasse kvadranti langeb üksjagu punkte ning ristkülikute pindalade kogusumma on üsna väike. Alloleval joonisel on näha ilmne tugev seos x ja y vahel, aga korrelatsioonikordaja tuleb ligikaudu 0 (Pearsoni: 0,007; Spearmani: 0,009).

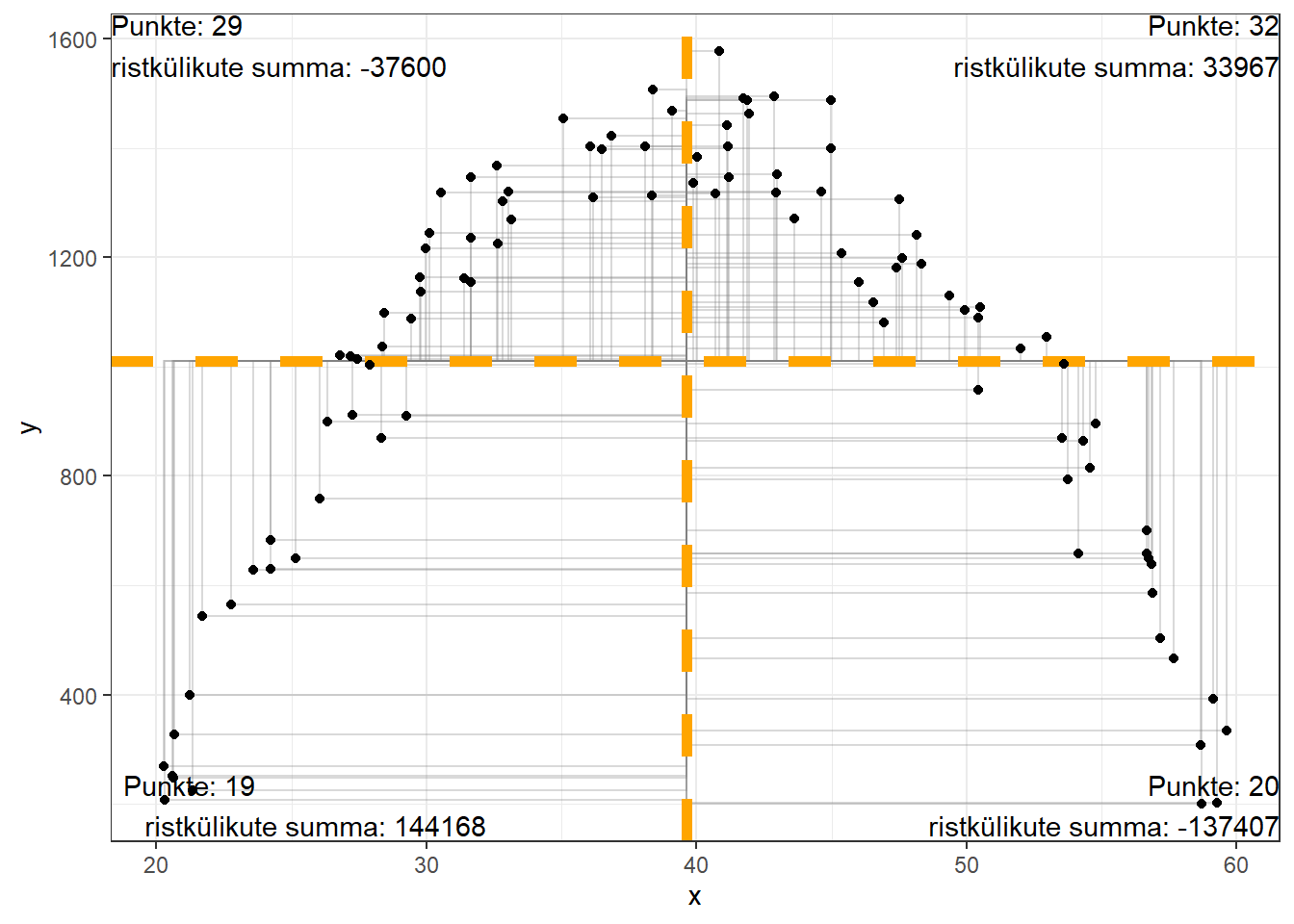
Ülemisel joonisel olevat seost ei saa kirjeldada sirge võrrandiga; öeldakse, et see seos x ja y vahel pole lineaarne. Seega korrelatskoonikordaja ei sobi mittelineaarsete seoste kirjeldamiseks.

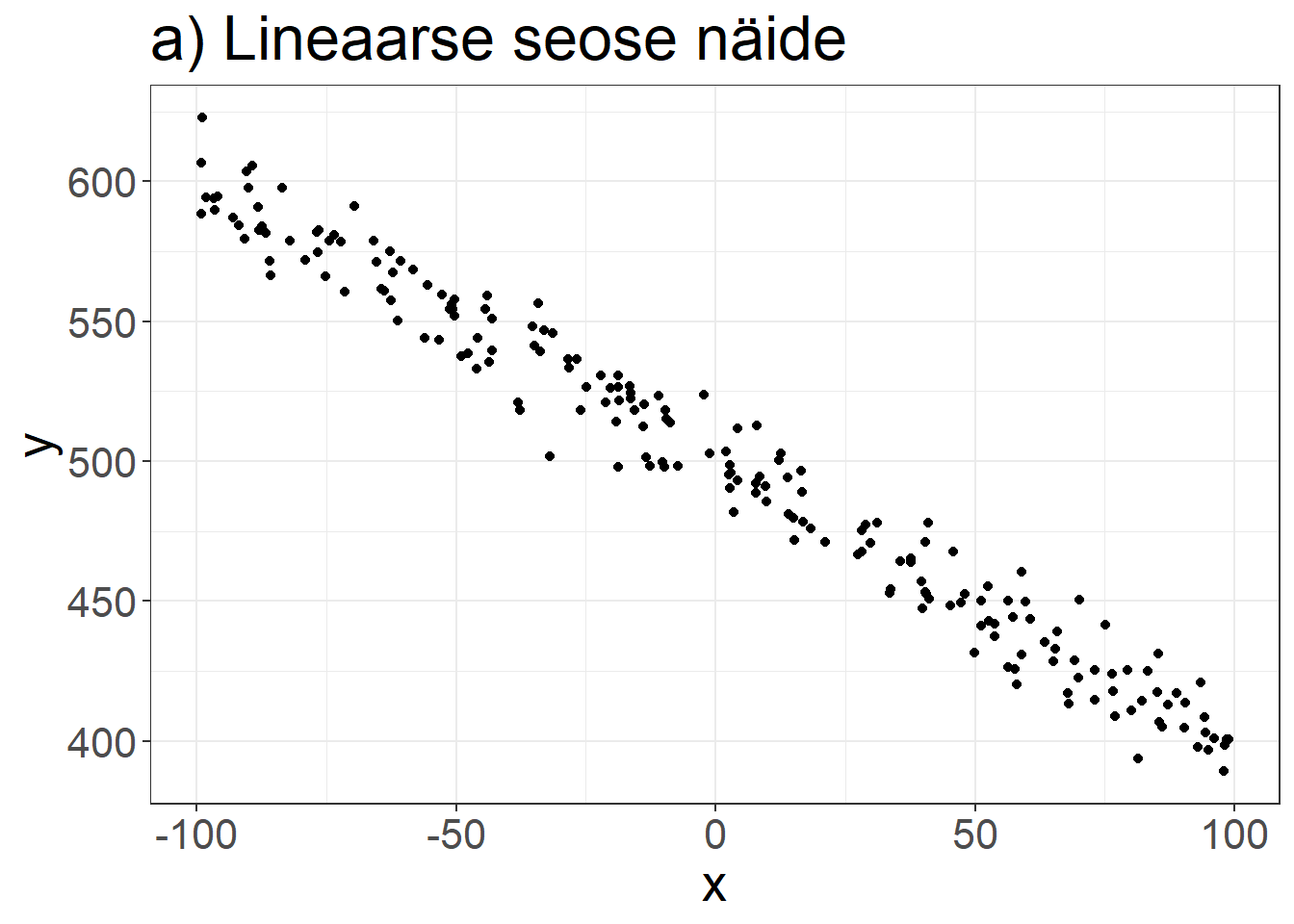
Väide 7.1 Pearsoni korrelatsioonikordaja iseloomustab lineaarse seose tugevust.

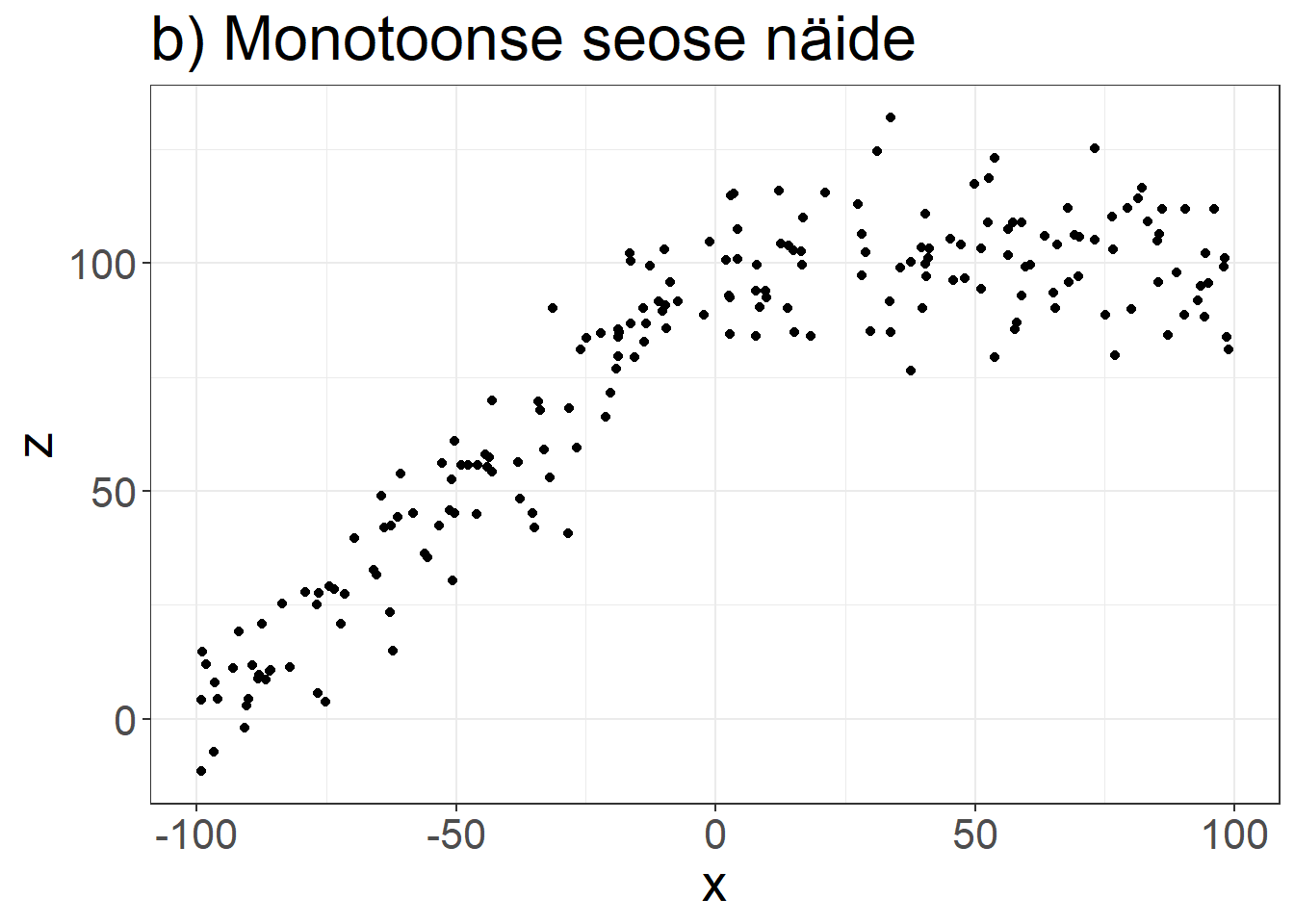
Spearmani astakkorrelatsioonikordaja iseloomustab monotoonse seose tugevust.

Lineaarne seos: ühe tunnuse väärtuse kasvades teise tunnuse keskmine väärtus ainult rangelt kasvab või rangelt kahaneb.

Monotoonne seos: ühe tunnuse väärtuse kasvades teise tunnuse keskmine väärtus ainult kasvab või ei kahane / ainult kahaneb või ei kasva.

Kuidas siis aga korrelatsioonikordajat tõlgendada? Väga rangeid kriteeriume pole, aga üldiselt

r	Tõlgendus
\(\approx 0\)	lineaarne seos puudub
\(\approx 1\)	tugev positiivne / võrdeline seos (ühe väärtuse suurenemisel teine väärtus suureneb)
\(\approx -1\)	tugev negatiivne / pöördvõrdeline seos (ühe väärtuse suurenemisel teine väärtus väheneb)
\(\approx 0,2\)	nõrk positiivne seos
\(\approx 0,5\)	mõõduka tugevusega positiivne seos

Osutub, et korrelatsioonikordaja teatud tüüpi teisendus (nn Fisheri z teisendus: \(z=1/2\ln(\frac{1+r}{1-r})\)) on ligikaudu normaaljaotusega keskväärtusega \(1/2\ln(\frac{1+\rho}{1-\rho}) + \frac{\rho}{2(n-1)}\) ja dispersiooniga \(1/(n-3),\) kus \(\rho\) on nn tegelik korrelatsioonikordaja (NB! hinnatav parameeter) üldkogumis.

Tänu sellele on võimalik arvutada ka korrelatsioonikordajale 95%-list usaldusvahemikku ning testida statistilist hüpoteesi \(H_0: \rho = \text{mingi arv}\) (\(\rho\) osundab nn tegelikule korrelatsioonikordajale üldkogumis).

All on mõningad korrelatsioonikordaja väärtused, millest alates võib (95%lise tõenäosusega) oletada, et üldkogumiski korrelatsioonikordaja \(\ne0\):

Valimi suurus	\(r\) kriitiline väärtus
10	0.55
20	0.38
50	0.24
100	0.16
250	0.10

Mõningad näited erinevate korrelatsioonikordajate kohta koos hajuvusdiagrammidega:

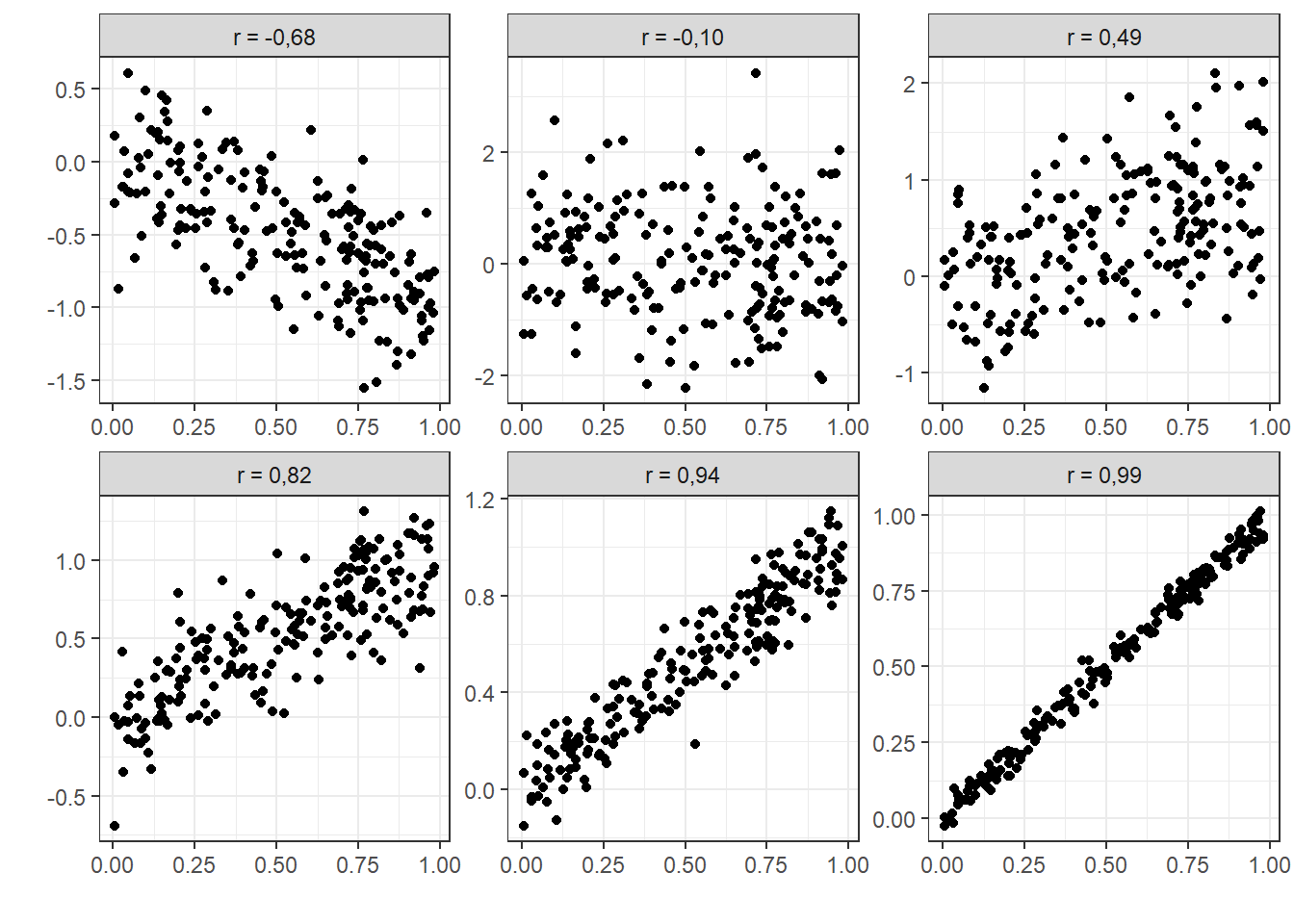
Kui korrelatsioonikordaja on 0, ei tähenda, et seos kahe tunnuse vahel puudub.

Kui korrelatsioonikordaja on tugev, ei näita see veel seose iseloomu täielikult. Alloleval kolmel joonisel on korrelatsioonikordaja kõigil ühesugune (0,98), aga x tunnuse väärtuse kasvades muutub y tunnuse väärtus väga erineva kiirusega.